
PID制御で速度を制御しようとしてるんだけど、なんか思うようにいかないな…?
PID制御で速度を扱う場合は、よくある位置制御とは少し勝手が変わるので注意が必要です。
このページでは、PID制御に速度が関わる場合の取り扱い方を、理論と具体例を交えて説明します。
※PID制御の基礎を未学習の方は、まずこちらのページをご覧ください
- 速度が関わる場合、制御対象の次数が変わるのでPID制御の動作イメージも変わる
- Iゲインは応答のばね定数、Pゲインはダンパ係数、Dゲインは質量のような働きをする
- このイメージを持ちながら、各種ゲインを調整すればOK
- Dゲインはほぼ不要なので、PI制御を基本に考えればよい
本質的に何が違うのか?
これまでのページでは、主に2次系を念頭にPID制御を解説してきました。2次系は、伝達関数の分母の次数が2となるシステムでしたね。
代表例としては、次のような機械システムが挙げられます。
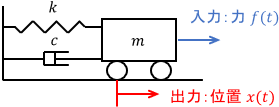
$$\begin{align}運動方程式\quad &m\ddot{x}(t) = -c\dot{x}(t) – k x(t) + f(t)\\[10pt] ラプラス変換して、 &X(s) = \ubg{\frac{1}{ms^2 + c s + k}}{伝達関数G(s)} F(s)\end{align}$$
入力は台車に加わる力$f(t)$、出力は台車の位置$x(t)$、$m$は台車の質量、$k$はばね定数、$c$は粘性係数です。
※その他の2次系の例については、こちらのページをご覧ください
ざっくりしたイメージでいうと、次のように入出力の次元が2階微分の関係にあれば対象は2次系であり、これまでの議論が適用可能です。
$$\osg{位置x}{出力} \ \color{black}{\xrightarrow{\large 微分}} \ 速度\dot{x} \ \color{black}{\xrightarrow{\large 微分}} \ 加速度\ddot{x}=運動方程式より\osg{力f}{入力}と同じ次元$$
実用上、PID制御の適用対象は2次系(または2次系に近似できるシステム)がほとんどなので、だいたいの場合はこれまでの解説を抑えておけば事足りるはずです。
ただし、PID制御に速度が関わる場合は、下で示すように入出力が1階微分の関係となります。これにより制御対象は1次系または積分系となるため、これまでの説明とは少し動作のイメージが変わるので注意が必要です。
ここからは、その詳細を理論と具体例で確認していきましょう。
制御に速度が関わる場合の数式モデル例
まず、制御に速度が関わる際に、対象システムの数式モデルがどうなるのかを確認していきます。
力で速度を制御する場合
よくあるのが、力によって速度を制御したい場合です。例としては、次のような機械システムが挙げられます。
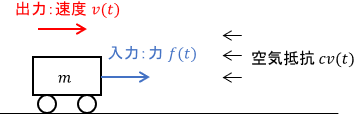
入力は台車に加わる力$f(t)$、出力は台車の速度$v(t)$、$m$は台車の質量、$c$は空気抵抗の係数です。この台車の運動方程式を求めると、次式が得られます。
$$m\dot{v}(t) = -cv(t) + f(t)$$
1階の微分方程式となっていますね。これをラプラス変換し、出力についてまとめると、伝達関数が得られます。
$$V(s) = \ubg{\frac{1}{ms+c}}{伝達関数G(s)} F(s)$$
伝達関数の分母の次数が1なので、この制御対象は1次系であることが分かりますね。抵抗がない場合、すなわち$c=0$の場合は、単純な積分系になることにも注意して下さい。
どちらにせよ、入出力は次のような1階微分の関係にあることになります。
$$\osg{速度v}{出力} \ \color{black}{\xrightarrow{\large 微分}} \ 加速度\dot{v}=運動方程式より\osg{力f}{入力}と同じ次元$$
速度で位置を制御する場合
速度によって位置を制御したい場合も、たまにあります。
機械システムは本質的には力で駆動されるものですが、例えば既存の設備が入力として速度(速度司令)しか受け付けてくれない場合などがこれにあたるでしょう。
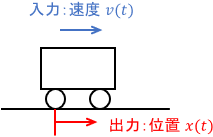
入力は台車速度$v(t)$、出力は台車の位置$x(t)$です。これらの入出力関係は、単純に次式で表されます。
$$\dot{x}(t) = v(t)$$
これをラプラス変換し、出力についてまとめると、伝達関数が得られます。
$$X(s) = \ubg{\frac{1}{s}}{G(s)}V(s)$$
シンプルな積分系となりました。この場合も、入出力は次のような1階微分の関係を持ちますね。
$$\osg{位置x}{出力} \ \color{black}{\xrightarrow{\large 微分}} \ \osg{速度v}{入力}$$
1次系に対するPID制御器の働き
それでは、制御対象が上述のように表されたとき、PID制御器がどのように作用するのかを数式で見ていきましょう。まずは1次系を例に考えていきます。
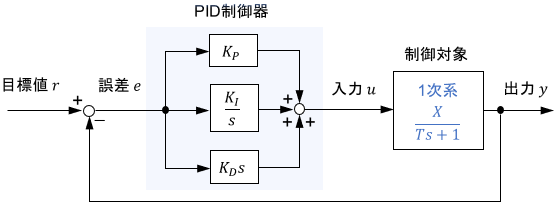
閉ループ伝達関数の導出
フィードバック制御システムの制御性能を確かめるには、目標値と出力の関係、つまりシステムの閉ループ伝達関数を見ればよいのでしたね。
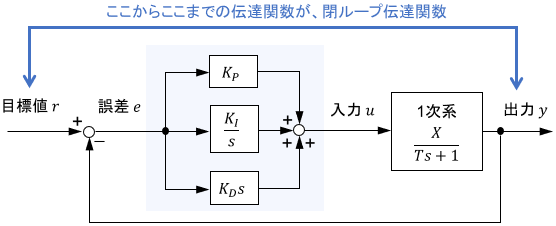
※閉ループ伝達関数の詳細については、こちらのページをご覧ください
今回のケースにおける閉ループ伝達関数を、具体的に計算していきましょう。
まず、次のようなフィードバック制御システムの閉ループ伝達関数$G(s)$は、次式で計算できることが知られています。

$$G(s) = \frac{C(s)P(s)}{1+C(s)P(s)}$$
今回のケースでは、制御器$C(s)$はPID制御器、制御対象$P(s)$は1次系ですね。
$$\begin{align}\mathrm{PID}制御器:&C(s) = K_P + \frac{K_I}{s} + K_D s = \frac{K_D s^2 + K_P s + K_I}{s}\\[7pt] 1次系:&P(s) = \frac{X}{Ts+1}\end{align}$$
定数$K_P,K_I,K_D$はそれぞれP・I・Dゲイン、定数$X,T$はそれぞれ1次系のゲインと時定数です。これらを閉ループ伝達関数$G(s)$の式に代入して整理すると、次式が得られます。
$$G(s) = \frac{K_D s^2 + K_P s + K_I}{(K_D + \frac{T}{X})s^2 + (K_P+\frac{1}{X})s + K_I}$$
この式によって、目標値$r$に対して出力$y$がどのように反応するかが表されているわけですね。
PIDゲインのイメージ
それでは、導出した閉ループ伝達関数を用いて、1次系に対してPIDゲインがどのように作用するのかを見ていきましょう。
$$G(s) = \frac{K_D s^2 + K_P s + K_I}{(K_D + \frac{T}{X})s^2 + (K_P+\frac{1}{X})s + K_I}$$
分母の次数が2なので、システム全体は2次系として動作することが分かりますね。2次系なので、パラメータ次第では振動的な応答をすることになります。
※2次系の基本性質については、こちらのページをご覧ください。今回はシステムが零点を持つため、厳密には零点のない2次系とは動作が少し変わります。ただ動作の本質は極で決まるため、基本性質は零点のない2次系と同じだと考えてOKです。フィードバックにより零点が生じる理由については、下のページをご覧ください。
PIDゲインが振動に及ぼす影響を、直感的に確認していきましょう。まず、振動する2次系の典型例として、先ほども出た機械システムを考えます。

入力は台車に加わる力$f(t)$、出力は台車の位置$x(t)$、$m$は質量、$k$はばね定数、$c$は粘性係数です。このシステムの伝達関数$\hat{G}(s)$と、先ほどの閉ループ伝達関数$G(s)$の分母の係数を比較してみましょう。
$$\hat{G}(s) = \frac{1}{\color{red}{m}s^2 + \color{red}{c}s + \color{red}{k}}, \quad G(s) = \frac{K_D s^2 + K_P s + K_I}{\color{red}{(K_D + \frac{T}{X})}s^2 + \color{red}{(K_P+\frac{1}{X})}s + \color{red}{K_I}}$$
| $\hat{G}(s)$の係数 | $G(s)$の係数 | 主な役割 |
|---|---|---|
| ばね定数$k$ | $K_I$ | 振動の速さを決める |
| 粘性係数$c$ | $(K_P + \frac{1}{X})$ | 振動の減衰特性を決める |
| 質量$m$ | $(K_D + \frac{T}{X})$ | 応答の「動きにくさ」を決める |
Iゲインがばね定数$k$、Pゲインが粘性係数$c$、Dゲインが質量$m$に対応していますね。制御対象が2次系のときは、Pゲインがばね定数、Dゲインが粘性係数のイメージで議論できていましたが、それらの対応が1つずつずれているような関係となっているのがポイントです。
PIDゲインの働き
各種PIDゲインのイメージがわかったので、これらの具体的な働きを見ていきましょう。
結論から言うと、それぞれのゲインの働きは、次のようにまとめられます。
- Iゲインが大きい:入力が大きくなり、動作は素早く、振動的になる。
- Pゲインが大きい:ブレーキ力が大きくなり、振動が抑制される
- Dゲインが大きい:動作が鈍くなる。ただしさらに大きくなるにつれ、異常に動作が速くなる
Iゲインはばね定数、Pゲインは粘性係数の作用そのままなので、イメージしやすいですね。
現実的には「Iゲインをなるべく上げて動作を素早くし、生じる振動をPゲインで抑制する」という使い方をすることになるでしょう。そのため、理想的な応答を得るためには、Iゲイン・Pゲインは大きな値を取ることになると言えます。
一方で、Dゲインは少しイメージがしにくいですね。Dゲインは質量のような作用をするため、大きくするほどシステムが「重く」なり応答が鈍くなります。
また、Iゲイン・Pゲインが大きい状態でDゲインをさらに大きくすると、閉ループ伝達関数$G(s)$が1に近づいていきます。
$$G(s) = \usr{\frac{K_D s^2 + K_P s + K_I}{(K_D + \color{red}{\frac{T}{X}})s^2 + (K_P+\color{red}{\frac{1}{X}})s + K_I}}{ゲインが大きいほど、これらの影響が小さくなる} \approx 1$$
伝達関数が1であれば$y=r$となるので、どんな目標値にも一瞬で追従できることになります。制御性能としてはこの上ない状態に見えますね。
ただし、後のシミュレーション例でも示す通り、「どんな目標値にも一瞬で追従」を実現しようとすると、システムに莫大な入力(負荷)を加える必要が生じるため、実用性という観点ではあまりよくない状態であるとも言えます。
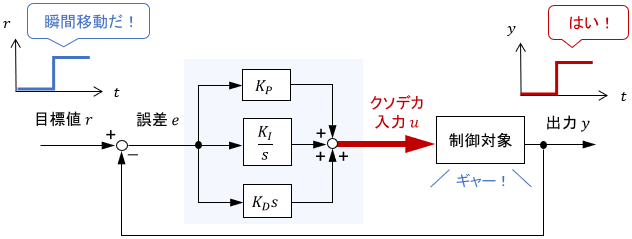
以上の通り、Dゲインを大きくしても大したメリットはないので、Dゲインは小さい値でよい(というか無くてもよい)と言えるでしょう。
定常特性
最後に定常特性についても見ておきましょう。定常特性は、閉ループ伝達関数ではなく内部モデル原理を用いた方が簡単に確認できます。
内部モデル原理は、「制御器$C(s)$か制御対象$P(s)$のどちらかが積分要素$\frac{1}{s}$を持っていれば、ステップ目標値(一定の目標値)に対する定常偏差を0にできる」というものでした。
今回は制御対象$P(s)$が1次系であり、積分要素を持っていません。よって、制御器が積分要素を持たないかぎり、すなわちIの項を持たないかぎり、応答には定常偏差が生じてしまうことが分かります。
$$\begin{align}&P(s) = \frac{X}{Ts+1}\quad \color{red}{積分要素なし}\\[5pt] &C(s) = K_P + \frac{K_I}{s} + K_D s = \frac{K_D s^2 + K_P s + K_I}{\color{red}{s}}\quad \color{red}{Iの項があれば積分要素を持つ}\end{align}$$
2次系の場合と変わらず、定常偏差をなくす役割はIの項が持つ、というわけですね。
以上より、1次系に対してPID制御を適用する際は、Dの項を省いたPI制御器を基本に考えればよいことが分かります。
※本来、内部モデル原理はステップ目標値以外にも適用できる理論です。詳細については、こちらのページをご覧ください。
シミュレーション例
それでは、数式にて確認したこれらの性質をシミュレーションで確かめてみましょう。
- 応答に振動が現れる
- ばねダンパ系で例えると、Iゲインがばね定数・Pゲインが粘性係数・Dゲインが質量として作用する
- Dゲインによるメリットはほぼないので、Dの項はなくてもよい
- Iの項があると、ステップ目標値に対して定常偏差なく追従できる

Iゲインの比較
振動の基本となるのは「ばねの作用」なので、まずはばねの作用を持つ(はずの)Iゲイン$K_I$を様々に設定して比較してみましょう。
Pゲイン$K_P$とDゲイン$K_D$は0に固定し、Iの項のみを使ってシミュレーションした結果がこちらです。(※$T=X=1$、目標値$r=1$です。以降も同様です)

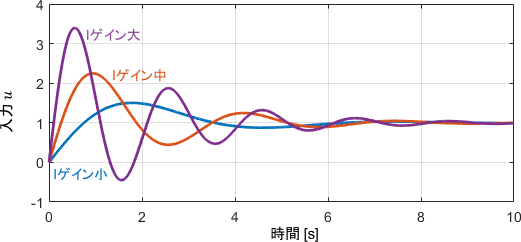
出力に注目すると、確かに振動が現れていますね。Iゲインの大小が振動の周波数の大小に対応しており、Iゲインがばね定数のような作用をしていることも分かります。振動の収束速度は、Iゲインの値に関わらず同じですね。
定常偏差に注目すると、Iの項のみのシンプルな制御とはいえ、積分要素を持っているので定常偏差0でしっかり追従できていることが分かります。
※上のグラフのような制御データの分析方法(着眼点)については、こちらのページをご覧ください。
Pゲインの比較
次に、Iの項によって生じた振動を抑えるために、ダンパの作用を持つ(はずの)Pゲインを様々に設定して比較してみます。Iゲインは先ほどの「中」設定にした上で、Pゲインを様々に変化させた結果がこちらです。

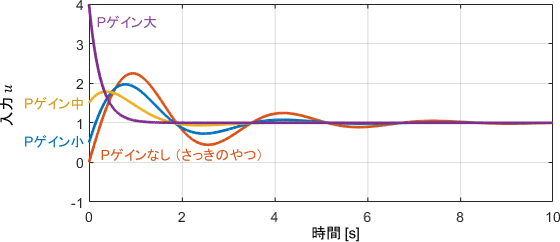
出力を見ると、Pゲインが大きいほど振動が抑制されていることが分かります。まさにPゲインがダンパの粘性係数のように働いている傾向が読み取れますね。
Iの項があるので、定常偏差が0なのもそのままです。
Dゲインの比較
最後にDゲインの影響を見ていきましょう。先ほど最もよさげな反応を示した「Pゲイン大」の設定で、Dゲインを様々に変化させた結果がこちらです。
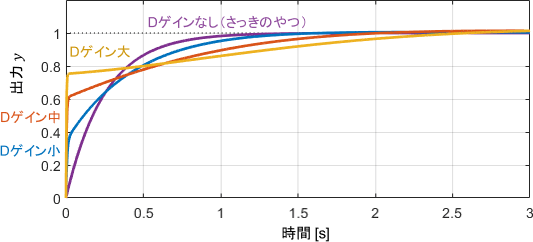
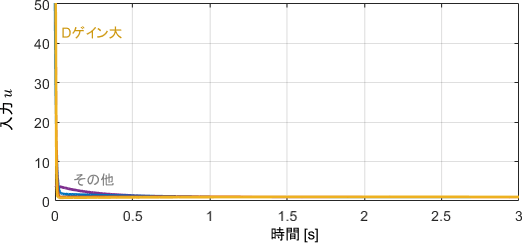
出力に注目すると、Dゲインが大きくなるほど立ち上がりが驚異的に速くなっていますね。前述のイメージではDゲインは質量のような作用を持つため、大きくなればなるほど動きが鈍くなるはずですが、それ以上に伝達関数が1に近づく作用が大きいため、結果的に反応が素早くなっていると解釈できます。
ただし、そのぶん出力の軌道が滑らかでなく、入力も非常に大きくなるため、システムにかなり無理をさせることになります。入力飽和を始めとした様々な悪影響が懸念されるため、前述の通りDゲインは小さくしたほうがよい(というか無くてもよい)と言えます。
積分系に対するPID制御器の働き
PIDゲインの働き
ここからは、制御対象が積分系で表される場合を考えていきます。
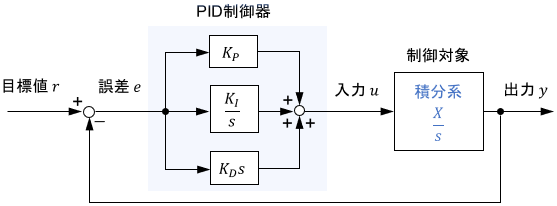
1次系の場合と同様の手順で閉ループ伝達関数$G(s)$を計算すると、次式が得られます。
$$G(s) = \frac{K_D s^2 + K_P s + K_I}{(K_D + \frac{1}{X})s^2 + K_Ps + K_I}$$
分母の次数が2となり、各種ゲインが先ほどの場合と同じようにかかっています。よって、PIDゲインの基本的な作用は1次系の場合と同じと考えてOKです。つまり、Iゲインがばね定数、Pゲインが粘性係数、Dゲインが質量のイメージですね。
1次系との違い
一方で大きく異なる点としては、定常特性が挙げられます。積分系は積分要素を持つ(というか積分要素そのもの)なので、内部モデル原理より「制御器がIの項を持たなくても、ステップ目標値に対する定常偏差が0になる」ことが分かります。
$$\begin{align}1次系&:P(s)=\frac{X}{Ts+1}\\[7pt] 積分系&:P(s)=\frac{X}{\color{red}{s}}\qquad \color{red}{積分要素を持つ!}\end{align}$$
よって、1次系の場合はPI制御が基本となっていましたが、積分系の場合はP制御だけでもよいことになります。
P制御、つまりPの項だけで積分系を制御した際の性質について、もう少し詳しく確認してみましょう。先ほどの閉ループ伝達関数にて$K_I=K_D=0$とすれば、P制御時の閉ループ特性が分かります。
$$G(s) = \frac{K_D s^2 + K_P s + K_I}{(K_D + \frac{1}{X})s^2 + K_Ps + K_I} = \frac{ K_P s }{ \frac{1}{X}s^2 + K_Ps} =\frac{ K_P }{ \frac{1}{X}s + K_P}$$
$s$が約分され、次数が1となりました。よって、システム全体は1次系として動作することになります。
1次系ということは、出力が絶対に振動しないことが分かりますね。これは嬉しい性質です。
※1次系の基本性質については、こちらのページをご覧ください。
以上より、制御対象が積分系の場合は、Pの項だけで「振動も定常偏差もない制御」が実現可能であり、かなりお手軽に制御できることが分かります。
ただし、たとえ制御対象が積分要素を持っていても、制御器が積分要素を持っていなければ、外乱がある場合に結局定常偏差が生じてしまうことには注意して下さい。

外乱による定常偏差も0にしたい場合は、Iの項を加えてPI制御を使用しましょう。その場合、各ゲインの働きは1次系の場合と同じです。
※外乱と積分要素の関係については、こちらのページをご覧ください。
シミュレーション例
それでは、数式にて確認したこれらの性質をシミュレーションで確かめてみましょう。
積分系にP制御を適用した場合、
- 絶対に振動しない
- ステップ目標値に対して定常偏差なく追従できる
- 外乱があると定常偏差が生じる

Pゲインの比較
P制御なので、Pゲインのみを様々に変化させたときの挙動を比較しましょう。

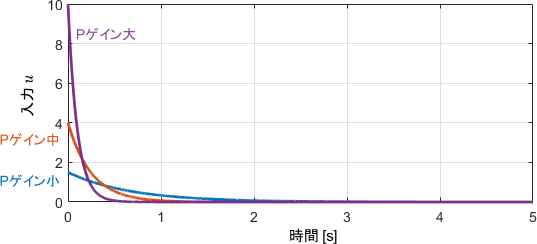
まず出力$y$に注目すると、確かに振動が全く生じていないことが分かります。定常偏差もしっかり0になっていますね。
また、Pゲインが大きいほど目標値への収束が速いことが見て取れます。ただし入力$u$も大きくなるので、Pゲインはシステムの能力の範囲内でなるべく大きな値を設定するのがよいと言えるでしょう。
外乱がある場合
続いて、入力に外乱が乗る条件でシミュレーションしてみます。Pゲインを先ほどの「中」設定にして、シミュレーションした結果がこちらです。
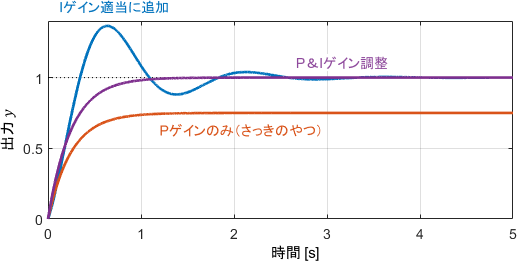
数式で確認した通り、Pゲインのみでは定常偏差が生じていますね。定常偏差を解消するには、Iの項を追加してPI制御にする必要があります。
そこで適当にIゲインを追加すると、Iゲインの「ばね」の作用が生じ、応答に振動が生じていることが見て取れます。ここからP&Iゲインをさらに調整することで、振動も定常偏差もない応答が得られていますね。
以上、PID制御にて速度が関わる場合についての解説でした。
- 速度が関わる場合、制御対象の次数が変わるのでPID制御の動作イメージも変わる
- Iゲインは応答のばね定数、Pゲインはダンパ係数、Dゲインは質量のような働きをする
- このイメージを持ちながら、各種ゲインを調整すればOK
- Dゲインはほぼ不要なので、PI制御を基本に考えればよい












コメント