ステップ入力に対するシステムの応答のことを、ステップ応答(またはインディシャル応答)と呼びます。ステップ応答は、システムの特性分析の基本中の基本として非常によく使われます。
このページでは、ステップ応答のイメージ・求め方・使い方を具体例を通じて解説します。
- ステップ応答は「システムに一定値を入力し続けるとどうなるか」を表したもの
- 厳密な応答が得やすく、かつ応答の意味が分かりやすいのが利点
- インパルス入力を積分するとステップ入力となる
- インパルス応答を積分するとステップ応答となる
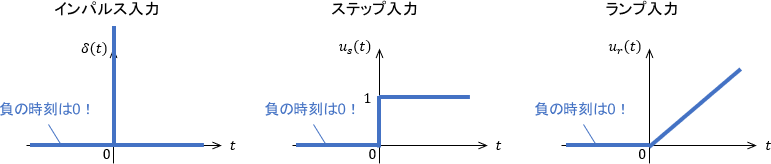
ステップ入力と単位ステップ関数
まず、ステップ応答を作り出すステップ入力について詳しく見ていきましょう。
ステップ入力は、次のような単位ステップ関数$u_s(t)$で表される入力です。
$$u_s (t) = \left\{ \begin{array}{ll} 1 &(0 \leq t)\\ 0 &(t < 0) \end{array} \right.$$
単位ステップ関数は$t=0$前後で不連続な関数です。ただ便宜上、不連続な部分も線でつないで下図のように描かれることが多いです。「ステップ」に見えるので「ステップ関数」というわけですね。


ステップ応答のイメージ
このステップ入力をシステムに与えたときの応答がステップ応答となります。この直感的イメージについて説明していきましょう。
といっても超簡単です。制御では$t=0$から動作が開始されると考えるので、「システムに1を入力し続けるとどうなるか」を表していると解釈すればOKです。

実用上は単位ステップ関数$u_s(t)$に何らかの値をかけて、任意の一定値を与えることがほとんどです。
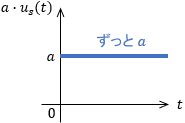

広義にはこれもステップ入力と呼ばれ、これに対するシステムの応答もステップ応答と呼ばれます。イメージとしては「システムに一定値を入力し続けるとどうなるか」ですね。
ステップ応答の具体例
それでは、ステップ応答の具体例を見ていきましょう。数学的な詳細は別ページで解説していますので、ここでは大まかなイメージが把握できればOKです。
機械システム
まず機械システムの例です。次のようなばねダンパ系を考えましょう。
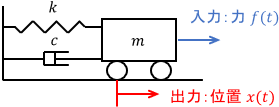

入力は力$f(t)$、出力は台車の位置$x(t)$です。よって一定の力$f(t)$を与えると、このシステムのステップ応答が得られます。


イメージとしては、台車を動かすモーターやエンジンを一定のパワーで駆動させたときの挙動ですね。
また重力はいつでも一定なので、次のようにシステムを縦向きに配置すると、重力をステップ入力$f(t)$とみなすこともできます。
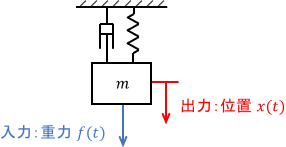

とにかく「一定の力に対するシステムの挙動」をイメージすればOKです。
電気システム
続いて、電気システムの例です。次のようなRC回路を考えます。
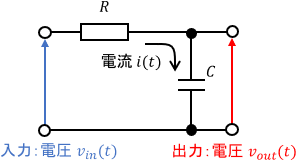

入力・出力はそれぞれ電圧$v_{in}(t),v_{out}(t)$です。よって一定の電圧$v_{in}(t)$を与えると、このシステムのステップ応答が得られます。


簡単に言うと、入力側のスイッチをずっと押しっぱなしにしたときの挙動ですね。
フィードバック制御システム
最後に、フィードバック制御システムの例です。先ほどのばねダンパ系を制御する、次のようなシステムを考えましょう。


入力は位置の目標値$r(t)$、出力は台車の位置$x(t)$です。
簡単に言うと、システムを一定の目標値に追従させたときの挙動ですね。一定目標値への追従は最も基本的な制御目的の1つなので、実用上非常によく使われるステップ応答です。
以上のように、入出力をどう設定するかによって入力や応答の物理的意味が変わるので注意してください。ステップ応答に限った話ではありませんが、システムの応答を見る上で重要なのは「自分が今どの信号の関係性を見ているのか」をしっかりと把握することですので、これを常に意識しておきましょう。
※ちなみに上のようなフィードバック制御システムでは、「どの信号の関係性を見ているのか」に応じて伝達関数の呼び方を変えることがあります。詳しくはこちらの記事をご覧ください。
ステップ応答の利点
先ほどの例の通り、ステップ入力は比較的簡単に作成できるため、厳密なステップ応答を現実に得やすいのが最大の利点です。インパルス応答はこういうわけにはいきませんでしたよね。
※インパルス応答の詳細は、こちらの記事をご覧ください。
さらに、分かりやすさと実用性を兼ね備えているのも利点です。
例えば先ほどの電気システムのステップ応答は「スイッチを入れ続けるとどう動くのか」を表していました。これは直感的に分かりやすいのはもちろん、実用シーンで非常によく生じる挙動ですよね。
また、フィードバック制御システムのステップ応答は「一定の目標値に追従させたときどう動くのか」を表していました。これを見るだけで、追従速度・追従誤差・振動の有無などの基本的な制御性能をだいたい把握できます。これも分かりやすい上に、実用シーンで非常によく使う挙動ですよね。


ステップ入力と積分は同じ?
ステップ入力を表す単位ステップ関数$u_s(t)$は、ラプラス変換すると$\frac{1}{s}$となります。
$$u_s(t) \ \xrightarrow{\large ラプラス変換} \ \frac{1}{s}$$


ラプラス変換で$\frac{1}{s}$って積分を意味するんじゃなかったっけ?
それがステップ関数ってどういうこと?
と思うかもしれません。ラプラス変換の定義に従って$u_s(t)$のラプラス変換を計算すれば、確かに$\frac{1}{s}$になることは確認できるのですが、それだけではイメージがつきにくいので、ここではより直感的な解釈を紹介しましょう。
※ラプラス変換や、その積分操作との関係については、こちらのページをご覧ください
一言でいうと、単位ステップ関数は単位インパルス関数を積分したものであり、$\frac{1}{s}$はその積分操作の名残であると解釈できます。順に説明していきましょう。
単位インパルス関数は、下図のようなものでした。(詳細は上で紹介したインパルス応答の記事をご覧ください)
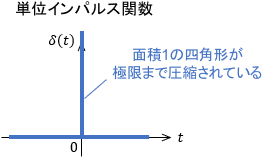

これを積分すると、単位ステップ関数になることを確認しましょう。積分なので、単位インパルス関数の面積を考えます。
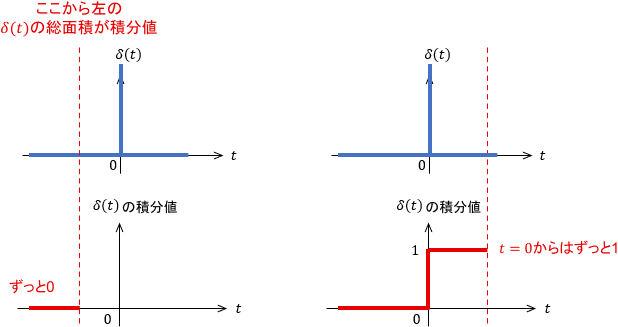

ピークが立つ前は面積0、ピークが立った後は面積1(=ピークの面積)なので、確かにステップ状になりますね。数式で表すと、次のようになります。
$$\usg{\int _{-\infty} ^t \delta(\tau) d \tau}{インパルス関数の積分} \usg{=\vphantom{ \int _{-\infty} ^t \delta(\tau) \tau }}{} \usg{u_s(t)\vphantom{ \int _{-\infty} ^t \delta(\tau) \tau }}{ステップ関数}$$
これをラプラス変換すると、次式となります。
$$\usg{1\vphantom{ \frac{1}{s}}}{インパルス関数} \cdot \usg{\frac{1}{s}}{の積分} \usg{=\vphantom{ \frac{1}{s}}}{} \usg{\frac{1}{s}}{ステップ関数}$$
単位インパルス関数はラプラス変換すると1になるため、積分操作の$\frac{1}{s}$だけが単位ステップ関数として残っているわけですね。
ステップ入力はインパルス入力の積分であると解釈すれば、混乱なく覚えられるでしょう。
※厳密には$\frac{1}{s}$の積分範囲は$\int _0 ^t$ですが、積分関係はより広い範囲である$\int _{-\infty} ^t$にも当てはまるため、上記のような説明をしています。負の領域まで考えている理由は、後ほど説明します。
ステップ応答とインパルス応答の関係
伝達関数$G(s)$で表されるシステムのステップ応答$Y(s)$を求めてみましょう。システムにステップ入力$U(s)=\frac{1}{s}$を与える、とステップ応答が得られます。
$$ステップ応答\ Y(s) = G(s)U(s) = G(s) \cdot \frac{1}{s}$$
一方、インパルス応答$Y_{\delta}$はインパルス入力$U_{\delta}(s)=1$を与えたときの挙動なので、伝達関数に等しくなるんでしたね。
$$インパルス応答\ Y_{\delta}(s) = G(s)U_{\delta}(s) = G(s) $$
上の2式を比べると、ステップ応答はインパルス応答の積分であることが分かります。
$$ステップ応答\ Y(s) = G(s)U(s) = \usg{G(s)\vphantom{ \frac{1}{s}}}{インパルス応答} \cdot \usg{\frac{1}{s}}{の積分}$$
入力だけでなく出力にも積分関係が成り立つというわけですね!逆に言うと、ステップ応答を微分すればインパルス応答を導出できます。この関係性は知っていると何かと便利なので覚えておきましょう。
定数なのに「ステップ」入力?負の時刻の意味は?


$t=0$から入力が一定なら、ステップ入力じゃなくて一定値入力じゃん。
なんで「ステップ」入力というの?
と思うかもしれません。確かにその通りで、「負の時刻で入力が0」としているから関数がステップ状に見えているわけですよね。制御では$t=0$から制御開始時刻とみなすのに、わざわざ負の時刻まで定義するのはなぜでしょうか?


この理由を一言でいうと、こうすることで数学的に全部辻褄が合い、取り扱いが非常に簡単になるからです。
例えばラプラス変換には移動定理といって、信号が作用する時刻を簡単にずらせる便利な演算があります。具体的には、$t$領域で信号を$a$だけ遅らせたいとき、$s$領域で信号に$e^{-as}$をかけるだけでこれを実現できます。
$$\ubgd{u_s(t-a)\vphantom{ \frac{1}{s}}}{ステップ入力を}{a遅らせたもの}\quad \xrightarrow{\large ラプラス変換}\quad \frac{1}{s} \cdot \ubgd{e^{-as}\vphantom{ \frac{1}{s}}}{これをかける}{だけで遅れる!}$$
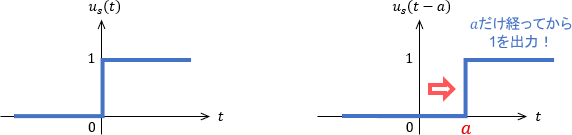

これを用いてステップ入力を遅らせると、無意味だと思っていた負の時刻の信号が表舞台に現れます。
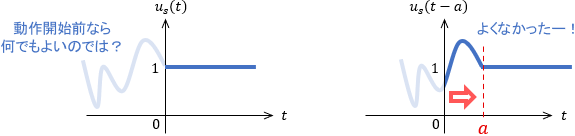

当然変な信号が出てくると困るので、色々と不都合が起きないよう、負の時刻もきちんと信号を定義する必要があるというわけですね。
詳しい説明は省略しますが、結論を言うと負の時刻で信号を0にしておけば、数学的に不都合が生じないことが知られています。こうすることで、例えば上図のように信号を$a$だけ遅らせる場合は、結局「時刻$a$が来るまで何もしない」ということになります。直感的にも違和感がありませんね。
ちなみにこれはステップ入力に限らず、インパルス入力やその他全ての信号に当てはまりますので、頭の片隅に置いておいてくださいね。

以上、ステップ応答のイメージ・求め方・使い方でした。
※こちらのページでは、主要なシステムのステップ応答について詳しく解説していますので、合わせてご覧ください
- ステップ応答は「システムに一定値を入力し続けるとどうなるか」を表したもの
- 厳密な応答が得やすく、かつ応答の意味が分かりやすいのが利点
- インパルス入力を積分するとステップ入力となる
- インパルス応答を積分するとステップ応答となる








コメント