このページでは、ボード線図の概要と利点について解説します。また、ゲインを表すデシベル値の読み方についても詳しく解説します。
- ボード線図は、システムの周波数特性を表現する図
- 振幅変化を示すゲイン線図と、位相変化を示す位相線図が2つセットになっている
- 広い範囲の周波数に対する特性を分かりやすく表現できるのが利点
ボード線図とは
ボード線図は、システムの周波数特性を表現する図の一種です。周波数特性を表す図には様々なものが提案されていますが、ボード線図はその中でも最も広く用いられており、制御設計において非常に重要な役割を担っています。
周波数特性は、「様々な周波数のsin波入力に対し、出力の振幅と位相がどのように変化するか」というシステムの特性のことでしたね。
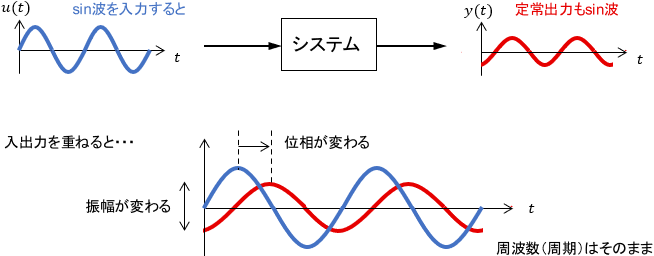
※周波数特性の詳細とイメージについては、こちらのページをご覧ください。
ボード線図は、次の2つのグラフをセットで使うことで、様々な入力周波数に対する周波数特性を図式的に表現します。
- ゲイン線図:横軸が入力信号の角周波数、縦軸がゲイン(出力の振幅が何倍になるか)
- 位相線図 :横軸が入力信号の角周波数、縦軸が位相(出力の位相が何度ずれるか)
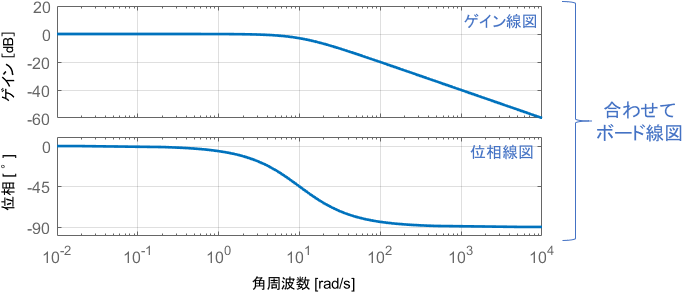
※通常、ボード線図の横軸は角周波数[rad/s]ですが、実用上は直感的に読みやすくするために横軸を周波数[Hz]で表すこともあります。どちらも単位が異なるだけで、結局は同じものを表しています。角周波数の詳細については、こちらのページをご覧ください。
ボード線図の読み方
横軸の読み方
ボード線図の横軸は、ゲイン線図・位相線図ともに入力信号の角周波数を対数目盛りで表したものとなっています。

対数目盛りなので、一定距離ごとに角周波数が倍々の法則で増えていきます。ちょうど目盛りを「一、十、百、千、万…」と読んでいくイメージですね。
横軸を対数目盛りで表すことで、広い範囲の周波数に対する特性を一気に表現できるのがボード線図の利点の一つです。
ちなみに、ボード線図中で角周波数が10倍になる距離は、1[decade]と表されます。”decade”は普通に読めば「ディケイド」ですが、なぜか制御では慣例的に「デカード」とダサい読み方で呼ばれます。
※対数目盛りの詳しい読み方と利点については、こちらのページをご覧ください。
ゲイン線図の読み方
続いて、ゲイン線図の縦軸の読み方です。ゲイン線図は、横軸にて表された様々な角周波数に対するゲイン(出力の振幅が何倍になるか)を対数目盛りで表したものとなっています。
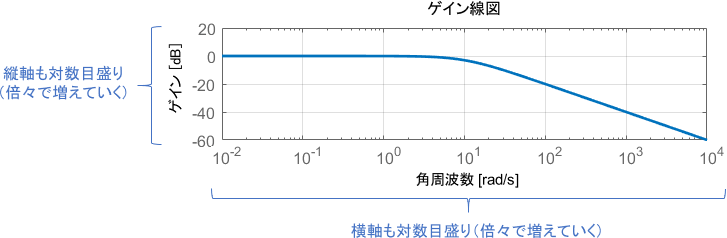
ただし、単位が[倍]ではなく[dB](デシベル)となっているのがポイントです。慣れていないと読み方がいまいち分かりにくいので、詳しく説明していきましょう。
デシベル表記の基本
デシベルは「ある量が、基準となる量に対して何倍か」を表す単位です。今回の場合は「出力の振幅が、入力の振幅に対して何倍になるか」をデシベル値で考えるわけですね。
まず、1倍はデジベル値で0dBとなります。つまり、基準となる量そのものですね。これを基準として、下図のように10倍ごとにデシベル値が20dBずつ増えていきます。

この法則でいくと、1000倍はデシベル値でいくらでしょうか?60dBですね!
なお、-20dBは対数目盛りを左向きに進むことになるので、$\frac{1}{10}$倍を表します。「行って戻ってくると同じ値になる」と考えると当たり前ですね。
※ちなみに音の大きさを表す単位もデシベルですが、これも本質的には同じものです。音の場合は「人間がギリギリ聞こえる大きさの音」を0dBとして、「それに対して何倍の大きさの音か」をデシベル値で表現しています。
代表的なデシベル値
上に出てきた20,40,60dBなどのキリのいいデシベル値は意味がわかりやすいですが、それ以外の値はどのように解釈すればよいでしょうか?ここでは、知っておくと便利な代表的なデシベル値についても紹介しておきます。
まず10dBを考えましょう。これは「2回進むと20dB(10倍)になる値」なので、$\sqrt{10}$≒3.16倍となります。だいたい3倍ですね。

また、6dBは2倍にほぼ等しいことも覚えておくと便利です。
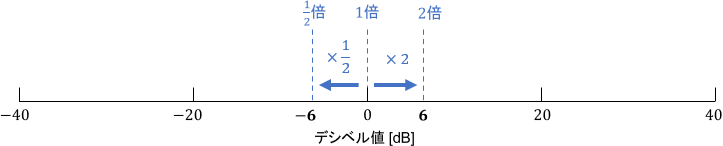
これらを組み合わせると、大体のデシベル値の倍率を見積もることが可能となります。
例えば26dBは20dB+6dBなので、10倍した後に2倍する、すなわち20倍を表すことが分かります。

また、16dBは10dB+6dBなので、約3倍した後に2倍する、すなわち約6倍を表すことが分かります。

デシベル値は足し算で増えていきますが、倍率は掛け算で増えていることに注意してくださいね。
下表に、代表的なデシベル値をまとめます。これらを組み合わせることで、大体のデシベル値は見積もれることでしょう。
| デジベル値 | 倍率 |
|---|---|
| -20dB | 0.1倍 |
| 0dB | 1倍 |
| 3dB | $\sqrt{2}$=1.41倍 |
| 6dB | 2倍 |
| 10dB | $\sqrt{10}$=3.16倍 |
| 20dB | 10倍 |
以上を踏まえて、先ほどのゲイン線図を読み取ってみましょう。
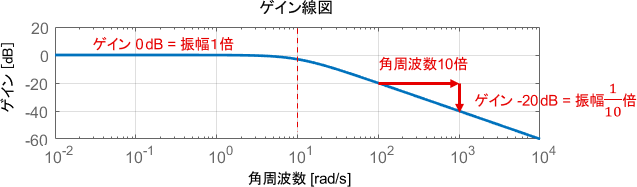
角周波数10[rad/s]を境にグラフが折れ曲がっていますね。
まず、10[rad/s]よりも低い角周波数では、だいたいゲインが0dB(つまり1倍)となっています。よって、10[rad/s]以下の角周波数のsin波を入力した場合、出力されるsin波の振幅は変わらないことが分かります。
次に、10[rad/s]よりも高い角周波数では、角周波数が10倍になるごとに(つまり1[decade]ごとに)ゲインが20dBずつ小さくなっています。よって、10[rad/s]以上の角周波数のsin波を入力した場合、角周波数が10倍になるごとに出力されるsin波の振幅は$\frac{1}{10}$になることが分かります。
位相線図の読み方
位相線図の縦軸の読み方に移りましょう。位相線図は、横軸にて表された様々な角周波数に対する位相(出力の位相が何度ずれるか)を普通の目盛りで表したものとなっています。

例として、この位相線図を詳しく読み取ってみましょう。
まず、$10^0=1$[rad/s]よりも低い角周波数では、だいたい位相が0°となっています。よって、1[rad/s]以下の角周波数のsin波を入力した場合、出力されるsin波の位相は変わらないことが分かります。
次に、$10^2=100$[rad/s]よりも高い周波数では、だいたい位相が-90°となっていますね。よって、100[rad/s]以上の角周波数のsin波を入力した場合、出力されるsin波の位相は90°後ろにずれる(遅れる)ことが分かります。縦軸が普通の目盛りなので、読み取りやすいですね!
位相において注意が必要なのは、位相が同じでも信号の周波数によって実質的なずれ(遅れ)の量は変わるという点です。
位相は「元のsin波1個分の長さを360°としたときに、それに対して信号のズレが何度分になるか」という相対的なものなので、元のsin波の長さが変わればズレの絶対量も変わるというわけです。

このような相対的な表現であるからこそ、シンプルなグラフでスッキリ位相を表現できているとも言えます。
ボード線図の利点
ここからは、ボード線図の利点をまとめて紹介します。ボード線図が周波数特性を表す図として、最も広く用いられている理由を把握しておきましょう。
利点1:システムの周波数特性をひと目で把握できる!
ボード線図は、とにかく見やすいのが最大の利点です。様々な周波数に対するシステムの特性を、これほどコンパクトかつ分かりやすく表現している図は他にありません。

まず、横軸を対数目盛りで表すことで、広い範囲の周波数に対する特性を一気に表現できていますね。さらに、横軸を統一しつつゲインと位相を別の図で表現することで、複雑になりがちな周波数特性を分かりやすく表現できているというわけです。
利点2:システムの安定余裕がわかる!
安定なフィードバック制御システムに対して
- ゲインがあと何dB上がるとシステムが不安定になるのか(ゲインにどれだけ余裕があるのか)
- 位相があと何度遅れるとシステムが不安定になるのか(位相にどれだけ余裕があるのか)
を、システムの安定余裕と呼びます。制御システムにとって安定性は大前提ですが、どれくらいの安定余裕があるのかを知っておくことも、非常に重要です。

ボード線図からは、この安定余裕も簡単に読み取ることが可能です。
※安定余裕の詳細については、こちらのページをご覧ください
利点3:システムが複雑でも書きやすい!
ボード線図は読みやすいだけでなく書きやすいため、実用性が非常に高いと言えます。

自分が取り扱うシステムのボード線図が手軽に書ければ、効率的にシステムを分析できますよね。
利点4:シンプルで超強力な便利法則がたくさんある!
ボード線図が書きやすいのは、ボード線図がシンプルで超便利な法則を多数持っているからです。これらの法則を知っていると、ボード線図を書くことはもちろん、読む際の理解も大きく深まります。
ボード線図の書き方と便利法則については、 こちらのページで詳しく解説していますので、合わせてチェックしてみてくださいね。
以上、ボード線図の読み方と利点についての解説でした!
- ボード線図は、システムの周波数特性を表現する図
- 振幅変化を示すゲイン線図と、位相変化を示す位相線図が2つセットになっている
- 広い範囲の周波数に対する特性を分かりやすく表現できるのが利点








コメント