このページでは、ボード線図の書き方と、ボード線図が持つ超強力な便利法則について解説します。
※ボード線図を書くには、ボード線図の基本的な読み方を理解しておく必要があります。ボード線図の読み方を未学習の方は、まずこちらのページをご覧ください。
- ボード線図には、読むのにも書くのにも超便利な法則がある
- それを使うと、大抵のボード線図は書ける
- 複数のシステムを組み合わせた際、システム全体のボード線図は、個別のボード線図を単純に足し合わせたものとなる
- 伝達関数の分母と分子をひっくり返すと、そのボード線図も0を境に上下がひっくり返る
ボード線図を書く方法
まず、ボード線図の書き方として、どのような選択肢があるのかを紹介していきます。
方法1:コンピュータに書いてもらう
今どきは、コンピュータが伝達関数からボード線図を瞬時に書いてくれます。何かシステムの伝達関数があるとき、とりあえずその周波数特性を把握するのに非常に便利です。
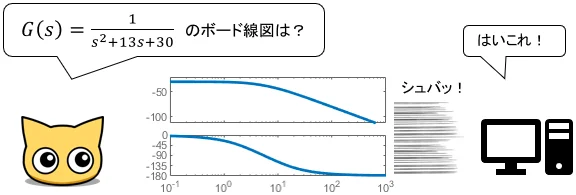

ただし、後で紹介するように、ボード線図は書く上で知っておくと便利な性質を持っています。これを知っていると、システムの理解や制御設計の効率が格段に上がるため、コンピュータに頼り切らず理論的な部分も理解しておくことをおすすめします。
※例えばこちらのサイトでは、入力した伝達関数に対し、ボード線図を含め様々な性質を自動で計算してくれます。
方法2:周波数伝達関数から書く
システムの周波数特性は、周波数伝達関数から計算できるのでした。具体的には、伝達関数$G(s)$で表されるシステムの周波数特性は、次のように計算できます。
- 角周波数$\omega$におけるゲイン=$|G(j\omega)|$
- 角周波数$\omega$における位相 =$\angle G(j\omega)$
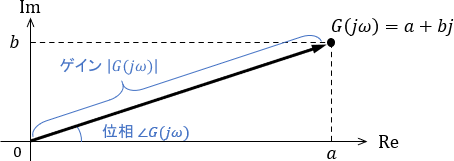

※$j$は虚数単位です。周波数特性の詳しい計算方法については、こちらのページをご覧ください。
ボード線図の横軸は角周波数$\omega$なので、ゲイン線図に$|G(j\omega)|$を、位相線図に$\angle G(j\omega)$をプロットすればそれがそのままボード線図となります。
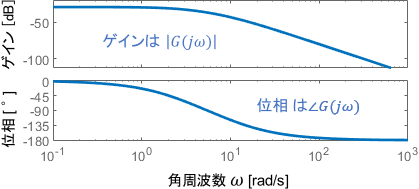

ただし、ゲイン$|G(j\omega)|$や位相$\angle G(j\omega)$の計算は複素数や複素平面を考える必要があるため、結構めんどくさいのが欠点です。
方法3:ボード線図の便利な法則を使って書く
ボード線図は、周波数伝達関数を計算しなくてもお手軽に書ける便利な法則を持っています。コンピュータを使わずにボード線図を書く場合は、この便利法則をフル活用する方法が主流です。
便利法則を知っていると、ボード線図が書けるだけでなく、ボード線図(システムの周波数特性)そのものの理解がすごく深まるため、しっかりと抑えておきましょう!
それぞれ順番に紹介していきます。
便利な法則1:足し合わせの法則
次のように複数のシステムを直列に組み合わせた際、システム全体のボード線図は個別のボード線図を単純に足し合わせたものとなります。


例を見ればすぐ意味が分かると思いますので、順番に見ていきましょう。
例1
次の2つのシステムを組み合わせた際の、ボード線図を考えてみましょう。
$$G_1(s) =\frac{1}{s+1},\qquad G_2(s)=\frac{1}{s}$$
$G_1(s)$は1次系、$G_2(s)$は積分系ですね。$G_1(s),G_2(s)$それぞれのボード線図と、それらを組み合わせた$G_1(s)G_2(s)$のボード線図は次のようになります。
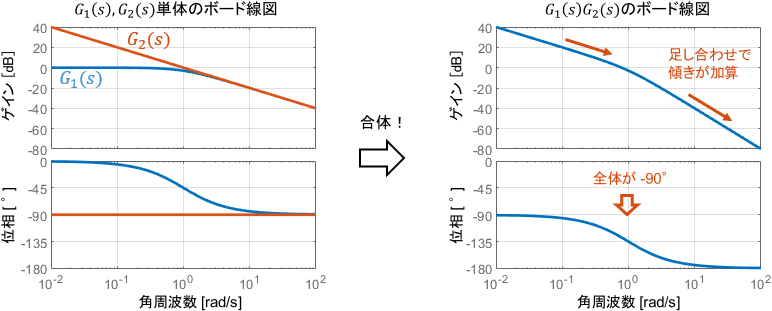

$G_1(s)$のボード線図に$G_2(s)$が足されることで、ゲイン線図の傾きが全体的に増加し、位相線図の値が全体的に減少していることが分かります。ゲイン・位相ともに、確かに$G_1(s)$と$G_2(s)$の値が足されたものになっていることも確認してみてくださいね。
例2
もう少し複雑な例として、次の2つのシステムの組み合わせも考えてみます。
$$G_1(s) =\frac{100}{s+1},\qquad G_2(s)=\frac{s}{0.01s+1}$$
$G_1(s),G_2(s)$それぞれのボード線図と、それらを組み合わせた$G_1(s)G_2(s)$のボード線図は次のようになります。
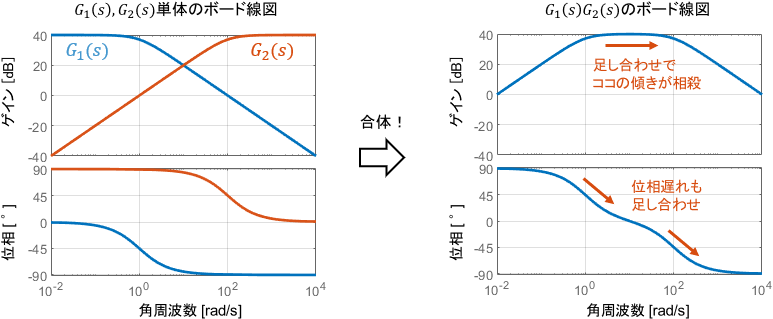

少し複雑ですが、結合後のボード線図がしっかり足し合わせになっていることが分かりますね。
高次系への応用
このように、複雑なシステムでも単純なシステムに分解し、それぞれのボード線図を足し合わせることで、比較的簡単にボード線図を書くことができます。
また高次系は、伝達関数の基本要素(比例要素・積分要素・1次遅れ要素・2次遅れ要素など)の組み合わせによって表現できることが知られています。よって、基本要素のボード線図を知っていれば、その組み合わせだけで様々なシステムに対応できると言えます。
※高次系と伝達関数の基本要素の関係については、こちらのページをご覧ください
以下に、特によく使われる基本要素のボード線図をまとめておきます。どれもシンプルですが、覚えておくと超便利です。
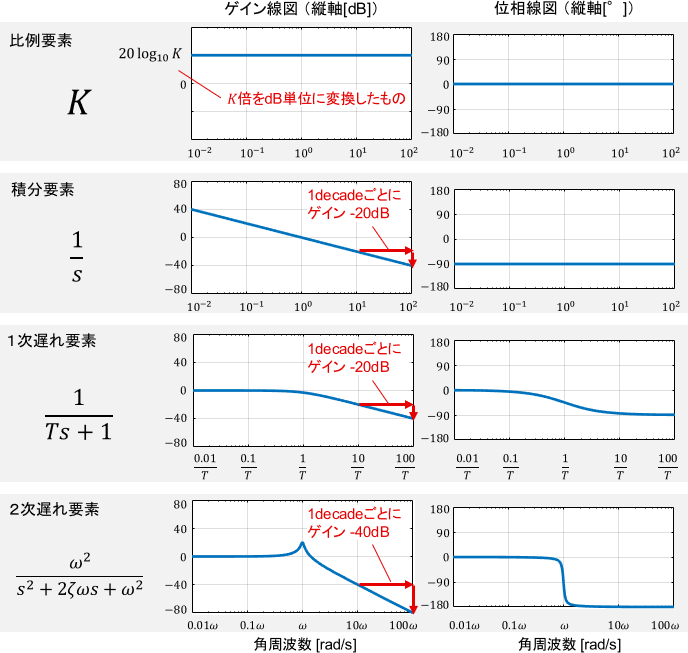

※基本要素のボード線図の詳細については、それぞれ個別の解説記事をご覧ください
便利な法則2:ひっくり返しの法則
伝達関数の分母と分子をひっくり返すと、そのボード線図も0を境に上下がひっくり返ります。
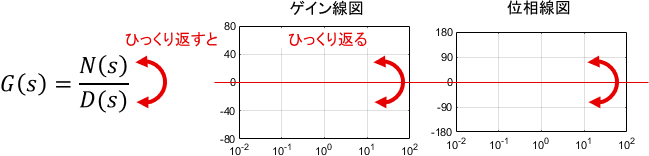

先ほどの基本要素にこの法則を適用した例を、下図に示します。
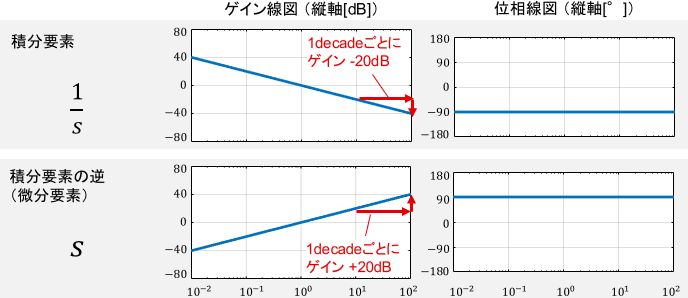

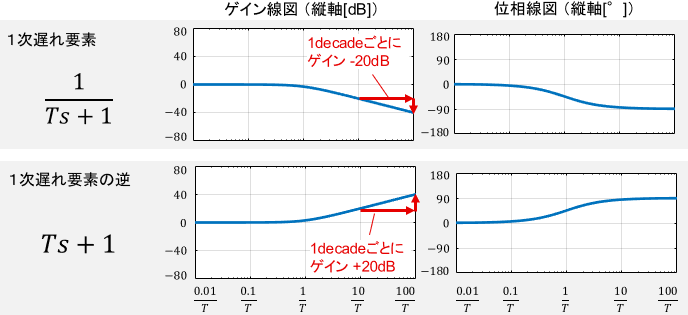

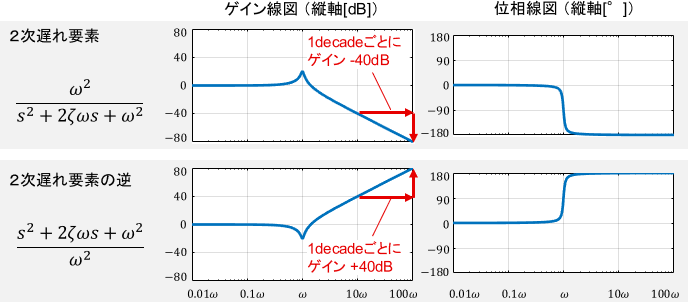

この法則と、先ほどの足し合わせの法則を組み合わせるだけで、古典制御にて取り扱う大抵のシステムのボード線図を描くことが可能となります。覚えることが少なくていいですね!
※微分要素のボード線図の詳細については、こちらのページをご覧ください
便利な法則3:ボードの定理
安定な極と零点のみを持つシステムは、最小位相系と呼ばれます。最小位相系に分類されるシステムに対しては、ボードの定理という便利な法則が成り立ちます。
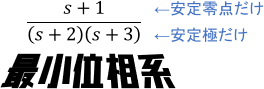
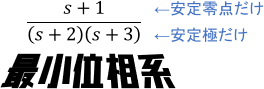
※極・零点、およびその安定性については、こちらのページをご覧ください
で、そのボードの定理ですが、簡単に言うと次のようにまとめられる法則です。
最小位相系のボード線図において、
- ゲインの傾きが 0dB/decadeで一定 ⇔ 位相は0°で一定
- ゲインの傾きが-20dB/decadeで一定 ⇔ 位相は-90°で一定
- ゲインの傾きが-40dB/decadeで一定 ⇔ 位相は-180°で一定
- ゲインの傾きが-20$k$dB/decadeで一定 ⇔ 位相は-90$k$°で一定
※ここでいう「一定」は、「2decade以上一定である」ことを意味する
これも例で見たほうが早いと思います。下図のように、ゲイン線図の傾きと位相に一定の関係がある、という法則です。
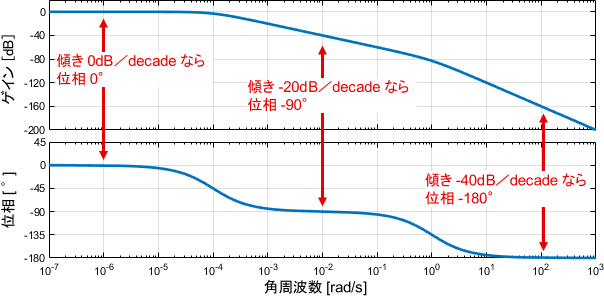

確かに、ゲインの傾き(または位相)が2decade以上一定であるエリアにて、上記関係性が成り立っていますね。
ボードの定理を知っていると、最小位相系に対しては、ゲイン線図単体からでも位相特性がだいたい分かることになります(その逆も然り)。
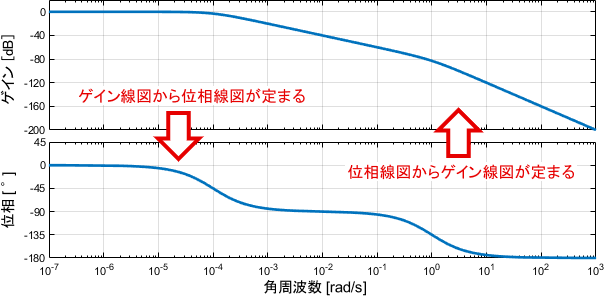

※厳密には、ボードの定理は上記よりも広い法則を説明したものとなっています。ただ、やたら複雑な数式で表され、その割には実用性が低いため、実用性のある上記法則に絞って紹介しています。
以上、3つの便利法則を紹介しました。
ちなみにこれらの法則が成り立つのは、ボード線図が対数目盛りを採用しているからです。対数目盛によって、ゲインや周波数の掛け算がグラフ上の足し算に変換され、全て辻褄があうようになっているわけです。よくできていますねー。
※ 対数目盛りの詳しい読み方と利点については、こちらのページをご覧ください。
読むときにも応用できる便利法則
上記便利法則たちは、ボード線図を書くときだけでなく、読むときにも非常に有用です。
例えば、他人が書いたボード線図がボードの定理を満たしていなければ、「何かおかしいぞ?」と気付くことができますよね。
他にも、各種法則を組み合わせることで、ボード線図を見るだけでシステムの伝達関数を推測することが可能です。
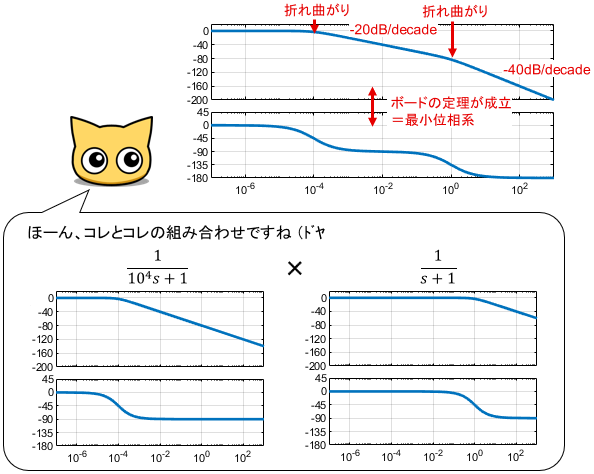

読むにも書くにも便利なボード線図が、非常に大きなポテンシャルを秘めていることが分かってきましたね!
以上、ボード線図の書き方と、便利な法則についての解説でした。
なお、実用シーンでボード線図をバリバリ使いこなすには、理想的なボード線図の形状や、実用上のコツを抑えておく必要があります。これについては、こちらのページで詳しく解説していますので、合わせてご覧ください。
- ボード線図には、読むのにも書くのにも超便利な法則がある
- それを使うと、大抵のボード線図は書ける
- 複数のシステムを組み合わせた際、システム全体のボード線図は、個別のボード線図を単純に足し合わせたものとなる
- 伝達関数の分母と分子をひっくり返すと、そのボード線図も0を境に上下がひっくり返る













コメント