このページでは、PID制御について、2次系を対象にその仕組みと動作イメージを解説します。
- PID制御は、使いやすさが最大の特徴。
- 面倒な計算をしなくても、80点くらいの性能を手軽に出せる。
- Pの項はバネ。出力を目標値に近づける、最も基本的な作用をする。
- Dの項はダンパ。出力の振動を防ぐ作用をする。
- Iの項は保持力。外乱に抗い、出力を目標値に留める作用をする。
PID制御とは
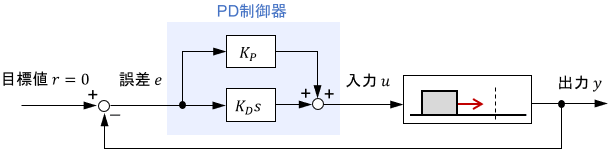
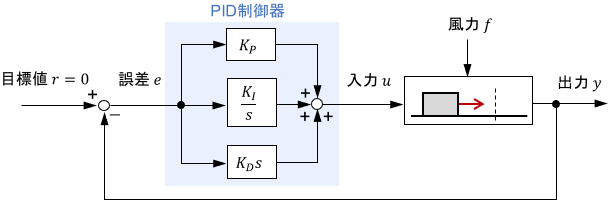
次のブロック線図(または数式)にて表される制御手法のことを、PID制御と呼びます。
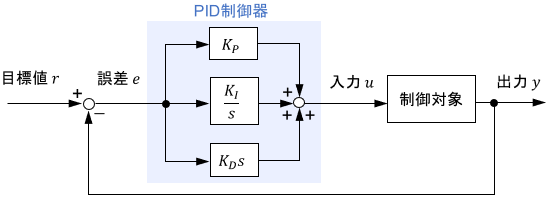
$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{比例\ P} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{積分\ I} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{微分\ D}$$
誤差$e$に対して、比例する項(Proportional)、積分する項(Integral)、微分する項(Derivative)からなるため、それぞれの頭文字をとって「PID制御」と呼ばれます。それぞれの項についている係数$K_P,K_I,K_D$は調整パラメータで、それぞれ「Pゲイン」「Iゲイン」「Dゲイン」と呼ばれます。
誤差$e(t)$を展開すると、上式は次のように変形できます。
$$u(t) = K_P\ubg{\bigl\{ r(t) – y(t) \bigr\} }{目標値と出力の差} + K_I \int ^t _0\ubg{ \bigl\{ r(\tau) – y(\tau) \bigr\}}{目標値と出力の差}d\tau + K_D\ubgd{\bigl\{ \dot{r}(t) – \dot{y}(t) \bigr\}}{目標値の微分と}{出力の微分の差}$$
例えば出力$y(t)$と目標値$r(t)$が位置情報である場合は、$\dot{y}(t)$は「実際の速度」、$\dot{r}(t)$は「目標速度」となります。よって、微分項の$\dot{e}(t)=\dot{r}(t) – \dot{y}(t)$は「目標速度と実際の速度の差」と解釈すればOKです。(それぞれの項の具体的な作用については、ページの後半で解説します)
PID制御器のブロック線図は、次のように1つにまとめて表されることもあります。

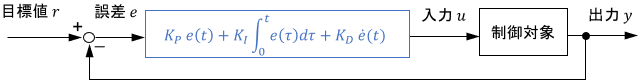
また、PID制御は有名なので、中身を知っている前提で次のように簡潔に表されることもあります。(ブロック線図は結局伝われば何でも良いので)

※ブロック線図の表現方法については、こちらのページをご覧ください
PID制御の特徴
PID制御は、その使いやすさが最大の特徴です。特に、「そこそこの性能でいいから、面倒な理論とか計算なしにシステムを動かしたい!」という場面によく使われます。その手軽さから「この世で使われている制御器の8割はPID」と言われるほど、非常に広く使用されています。
PID制御がこのような特徴を持つのは、調整パラメータが少なく、かつ調整がしやすいためです。これについて詳しく説明していきましょう。
PID制御の性能は、Pゲイン・Iゲイン・Dゲインの値によって決まります。これらのゲインを調整することは、PIDゲインチューニングと呼ばれます。
たかだか3つのパラメータを調整するだけでよいので、PIDゲインチューニングは実際に制御対象を動かしながら試行錯誤的にやることがほとんどです。そのため複雑な理論や計算は不要で、少しコツを知っていれば制御工学をよく知らない人でもお手軽に80点くらいの性能を出せてしまうことが多いです。

もちろん、システムの数式モデルを用いて理論的にチューニングすることも可能です。その場合はより高い性能が期待できますが、実用上は手作業で試行錯誤チューニングをすることがほとんどです。この理由としては、数式モデルには必ず誤差があるため結局最後には手作業でのチューニングが必要であることや、そもそもPID制御を使うときはそこそこの性能で良い場合が多いことが挙げられます。
最後に、PID制御の適用対象についても簡単に説明しておきましょう。PID制御は、基本的に単入力単出力のシステムに適用されます。
下のブロック線図のように多入力多出力システムに対してPID制御器を複数重ね合わせて対応することもありますが、設計難度やチューニング難度が上がってPID制御の手軽さが薄れるため、多入力多出力システムに対応した他の制御器を使う場合が多いです。
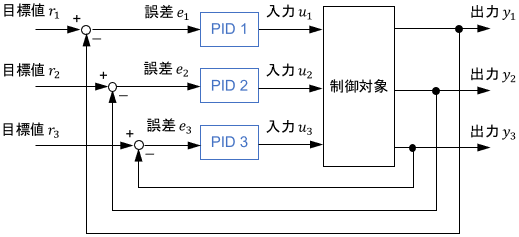
PID制御の動作イメージ
ここからは、簡単な機械システムの制御を例題に、PID制御の動作イメージを説明していきます。
次のように、空気抵抗を受けながら動くブロックに力を与え、位置を0に持っていくことを考えます。
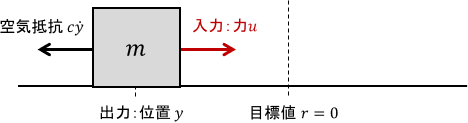
システムの入力はブロックに加わる力$u$、出力はブロックの位置$y$、目標値$r$は0($\dot{r}$も0)です。
運動方程式より、このシステムの伝達関数は次のように得られます。
$$G(s) = \frac{1}{ms^2 + cs}$$
分母の次数が2なので、2次系ですね。実用上、PID制御は2次系(または2次系に近似できるシステム)を対象とすることが非常に多いため、まずはこの例題のイメージを基本としてしっかり抑えておきましょう。
※その他の2次系の例は、こちらの記事をご覧ください。具体的なシステムが何であれ、対象が2次系であれば、その直感的イメージは以下の説明と同じです。
超シンプル制御
まずPID制御の前に、「ブロックが目標地点より手前にいれば前進方向に、奥にいれば後退方向に一定の力を入力する」という超シンプルな制御を適用してみます。数式で書くと次の通りですね。
$$u(t) = \left\{ \begin{array}{cl} f_c & \mathrm{if}\ 0<e(t) \\ -f_c & \mathrm{if}\ e(t)<0\end{array}\right.$$

$f_c$は力を表す定数です。この条件でシステムを制御すると、次のような挙動が得られます。

※矢印の長さが入力$u$の大きさを表しています(以降のアニメーションでも全部そうです)
0を跨ぐたびに入力の正負が急に切り替わるため、目標地点の近くでガクガク動くだけで、結局到達できていませんね…
以降、これを改善していく形で、PID制御の動作を順に見ていきましょう。
Pの項のイメージ
入力$u$の大きさが一定だとまずかったので、これを可変にしてみます。
PID制御のPの項(比例の項)を使うと、誤差が大きい(目標地点から遠い)ときには入力を大きく、誤差が少ない(目標地点に近い)ときには入力を小さくするように入力値を調整できます。
$$u(t) = \ubg{K_P\ e(t)}{Pの項} = K_P\bigl\{ r(t) – y(t) \bigr\} =\ – K_P\ y(t)\ \color{green}{(r=0なので)}$$
Pゲイン$K_P$は、調整パラメータです。このようにPの項だけを使った制御は、P制御と呼ばれます。

適当な$K_P$を用いてシステムを制御すると、次のような挙動が得られます。

先ほどと異なり、目標地点にしっかり到達できていますね!
Pの項は誤差(目標地点からの距離)に比例して力を決定するので、ちょうど目標地点とブロックをバネでつないだような作用をすることになります。そのばね定数が、Pゲイン$K_P$となっているイメージですね。
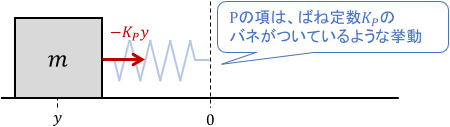
この作用の結果として、Pの項は「出力を目標値に近づける、最も基本的な役割をする」と解釈できます。
ただ、目標地点の近くを行ったり来たりと、振動的な挙動をしているのが気になりますね…。上記バネのイメージを持ちながら、この振動的な挙動を改善していきましょう。
Dの項のイメージ
P制御では、誤差(目標地点からの距離)のみを考慮にいれていましたが、本当は目標地点でピタッと止まってほしいわけですね。そこで、速度も考慮に入れることにしましょう。
PID制御のDの項(微分の項)を使うと、実際の速度が目標速度を上回るときにはブレーキをかけ、下回るときには加速するように入力を調整できます。ブレーキ(or加速)の大きさは、速度誤差の大きさに比例します。
$$\begin{array}{rlll}u(t)&= \ubg{K_P\ e(t) }{さっきのPの項} &\ + \ubg{K_D\ \dot{e}(t)}{Dの項}& \\[3pt] & =\ – K_P\ y(t) &+\ K_D\bigl\{ \dot{r}(t) – \dot{y}(t) \bigr\}& \\[7pt] & =\ – K_P\ y(t) &\ – K_D\ \dot{y}(t)& \color{green}{(\dot{r}=0なので)}\end{array}$$
Dゲイン$K_D$は、調整パラメータです。このようにPの項とDの項を使った制御は、PD制御と呼ばれます。
適当な$K_P,K_D$を用いてシステムを制御すると、次のような挙動が得られます。

YEAHHHHH!!!目標地点にスムーズに到達できていますね!
入力を表す矢印に着目すると、ブロックが目標地点に近づくにつれて、Dの項が「ちょっと今のままでは速すぎるよ」と言わんばかりにブレーキをかけてくれていることが分かります(左向きに伸びる矢印がそれです)。結果的に、目標地点到達($y=r=0$)と同時に、速度も目標値に等しくなっている($\dot{y}=\dot{r}=0$)わけですね。
Dの項は速度誤差(目標地点に対する速度)に応じて力を決定するので、ちょうど目標地点とブロックをダンパでつないだような作用をすることになります。そのダンパの粘性定数が、Dゲイン$K_D$となっているイメージですね。

この作用の結果として、Dの項は「振動的な挙動を抑制し、出力を滑らかに目標値に導く役割をする」と解釈できます。

ヤッター!これでいい感じの制御達成!
と思いたいところですが、これだけだとまだ問題があります。ブロックが外力を受ける場合です。
例として、次のように向かい風が吹いている場合を考えてみましょう。
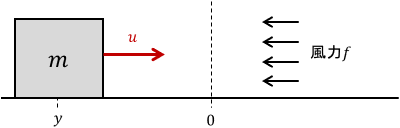
ブロックは常に一定の風力$f$を外力として受けますが、我々(制御器)はそれを知らないとします。この条件で上記PD制御を適用すると、次のような挙動が得られます。

風力に負けて、ブロックが目標地点に到達できていませんね…。制御入力$u$が風力$f$とちょうど釣り合い、立ち往生してしまっているわけです。
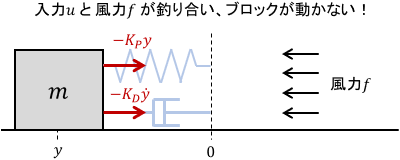
だいたい想像がついたかもしれませんが、今度はこれを改善していきましょう。
Iの項のイメージ
Pの項の「目標地点に向かおうとする力」だけでは外乱に抗えないことが分かったので、外乱に抗う仕組みを追加しましょう。それがPID制御のIの項(積分の項)です。
$$\begin{array}{rllll}u(t)&= \ubg{ K_P\ e(t) }{さっきのPの項} & + \ubg{ K_D\ \dot{e}(t)}{さっきのDの項}& +\ \ubg{K_I \int ^t _0 e(\tau) d\tau}{Iの項} & \\[3pt] & =\ – K_P\ y(t) &-\ K_D\ \dot{y}(t)& +\ K_I \int ^t _0 \bigl\{ r(\tau) – y(\tau) \bigr\} d\tau & \\[7pt] & =\ – K_P\ y(t) &-\ K_D\ \dot{y}(t)& -\ K_I \int ^t _0 y(\tau) d\tau & \color{green}{(r=0なので)}\end{array}$$
$\int ^t _0 e(\tau) d\tau$の部分がややこしく見えるかもしれませんが、簡単に言うと「制御開始時から今までの誤差の蓄積量(総和)」です。それが、Iゲイン$K_I$に比例する形で追加の力を生み出します。
例えば先ほどの例だと、風でなかなか進めない間にIの項にて誤差がどんどん蓄積し、結果的に「風に抗って進む力」が生まれることになります。
実際に見てみましょう。適当な$K_P,K_D,K_I$を用いてシステムを制御すると、次のような挙動が得られます。

※上部に出ているメーターが、Iの項によって発生している力($=K_I \int ^t _0 e(\tau) d\tau$)を表しています
3秒あたりから風の力で前に進めなくなっていますが、誤差の蓄積によりジワジワと追加の力が発生し、最終的に目標地点に到達できていますね。目標地点に到達すれば誤差は0なので、誤差の蓄積量が増えることもありません。
以上より、Iの項は「外乱に抗い、出力を目標値に保持する」役割を持つと解釈できます。
上の例ではイメージのしやすさのために誤差がじわじわ増えるようなIゲイン$K_I$を設定しましたが、より適切にゲインを設定すれば、次のように素早く目標値に到達させることが可能です。

これにてPID制御完成というわけですね!
※ちなみに、「なぜ積分要素(Iの項)が外乱に抗い出力を目標値に保持できるのか」や、「どのような目標値・外乱であればきちんと保持できるのか」は内部モデル原理という理論によって説明(証明)されています。詳しくは、こちらのページをご覧ください。
以上、PID制御の仕組みと動作イメージについての解説でした。
本ページでは直感的なイメージにフォーカスして解説しましたが、こちらのページではPIDゲインの値を様々に変えながら、その特性をより詳しく紹介していますので、合わせてご覧ください。
- PID制御は、使いやすさが最大の特徴。
- 面倒な計算をしなくても、80点くらいの性能を手軽に出せる。
- Pの項はバネ。出力を目標値に近づける、最も基本的な作用をする。
- Dの項はダンパ。出力の振動を防ぐ作用をする。
- Iの項は保持力。外乱に抗い、出力を目標値に留める作用をする。







コメント
電気主任技術者試験対策で勉強しております。
とても分かりやすくいつも助かっております。
しかしD項のイメージがまだ少しつかめておりません。
速度に比例してブレーキが掛かると理解しておりますが、それはざっくりしたイメージですができるだけ一定速度で目標に向かうようにするとも言えますでしょうか。
もしかしたらP制御とPD制御の時の速度グラフがあるとよりイメージがわくような気がしました。
ご活用いただき、ありがとうございます!
D項は「実際の速度が目標速度を上回るときにはブレーキをかけ、下回るときには加速する」というものですので、ページ内の例で言うと「一定速度で目標に向かう」という働きではなく「速度を0(=目標値)に収束させる」という働きをしていることになります。
P制御とPD制御の動作をグラフで比較すると、こちらのようになります。PD制御のほうが速度の大きさ(=目標値0からの乖離)が小さく、収束も早くなっていることが見て取れるかと思います。

