

PI制御・PD制御・PID制御とか色々あるけど、どう違うの?どう使い分ければいいの?
という疑問に答えるために、このページでは2次系を念頭に、それぞれの制御手法の特徴と選択指針について解説します。
PID系の制御ではゲインチューニングが重視されがちですが、ゲインチューニングは適切な制御器の選択が前提となっているため、選び方もしっかり抑えておきましょう!
- Pの項を基本として、必要に応じてI・Dの項を追加していけば必要な制御器が出来上がる
- Dの項が必要になるのは、システムに振動を抑制する要素が十分にない場合
- Iの項が必要になるのは、出力が目標値に留まるのを邪魔する何らかの作用が働く場合
- 余分な項を入れると制御性能が悪化しがちなので注意する
PI・PD・PID制御器とは
まず、基本をおさらいしましょう。PID制御におけるPの項・Iの項・Dの項それぞれの役割は、次の通りでしたね。
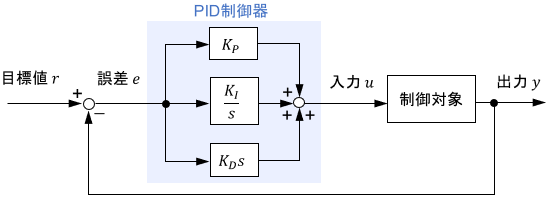

$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Pの項} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{Iの項} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Dの項}$$
- Pの項はバネ。出力を目標値に近づける、最も基本的な作用をする。
- Iの項は保持力。外乱に抗い、出力を目標値に留める作用をする。
- Dの項はダンパ。出力の振動を防ぐ作用をする。
※それぞれの役割の詳細については、こちらの記事をご覧ください。
このPID制御器からDの項を省き、PとIの項のみで構成される制御器はPI制御器と呼ばれます。また、Iの項を省き、PとDの項のみで構成される制御器はPD制御器と呼ばれます。
結局、PI制御器・PD制御器・PID制御器は別物ではなく、P・I・Dのうちどの項(機能)がついているかだけの違いであると理解すればOKです。


P・I・D項の選び方
Pを基準に必要な機能を追加!
となると、問題は「それぞれの項をどう選べばよいか」ですね。
ほとんどの場合は「最も基本的な作用をするP項は必須として、必要に応じてそれにI・Dの項を追加していく」という流れで考えるとよいでしょう。
それぞれの項の役割を考えると、Iの項・Dの項を追加すべきケースは次のようになります。
- Iの項:制御対象に定常偏差が生じ、それが問題となる場合
- Dの項:制御対象に振動が生じ、それが問題となる場合


自分のシステムがこれに当てはまるかどうかは、どうやって調べればいいの?
一番確実なのは「P制御だけで実際に動かしてみて、上記問題が生じるかを確認する」ことでしょう。
定常偏差や振動の有無はシステムの数式モデル(伝達関数)から計算することも可能ですが、数式モデルは現実のシステムを完璧に表したものではないため、完全に信用できるのはやはり実際の挙動のみとなります。

よって実用場面では、必ず実際のシステムを用いた動作確認を実施すべきです。
とはいえ「動かしてみないと分からない」では困るのも事実なので、ここからはI・Dの項が必要になる条件をイメージと理論で整理していきましょう。
Dの項が必要になる条件の直感的イメージ
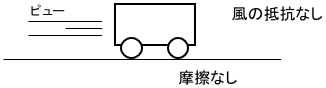
Dの項が必要になる場合、すなわち制御対象に振動が生じる場合としては、「システムに振動を抑制する要素が十分にない場合」をイメージすればOKです。
例えば機械システムの場合は、機械が大きな摩擦や抵抗なく動作する場合がこれに当たります。

※ちなみにDの項は、振動抑制以外にも、応答速度の向上等のために付加されることがあります。ただ実用上は振動抑制(安定性の向上)のほうが重要視されるので、Dの項は振動抑制に使われることがほとんどです。
Iの項が必要になる条件の直感的イメージ
Iの項が必要になる場合、すなわち制御対象に定常偏差が生じる場合としては、「出力が目標値に留まるのを邪魔する何らかの作用が働く場合」をイメージすればOKです。
例えば機械システムの場合は、目標値にて制御対象に力が働く場合がこれに当たります。
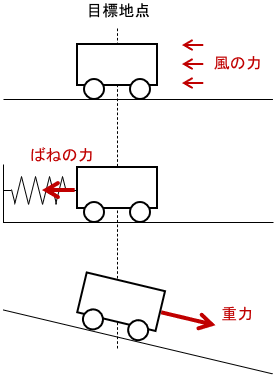

Iの項によってこの外力に抗う力を発生させ、定常偏差を解消するわけですね。
Iの項が必要になる理論的な条件
実用上は上記イメージを抑えておけば事足りることが多いですが、イメージを理論に紐付けて理解しておくと制御器設計の幅が広がりますので、余裕があれば抑えておきましょう。
※初めて学習する方は、この節は流し読みで構いません。ちなみに、Dの項の理論的な条件は結構複雑で実用性があまりないので省略します。
Iの項の必要性は内部モデル原理を用いることで、理論的に判断できます。
内部モデル原理は、次のようなものでした。
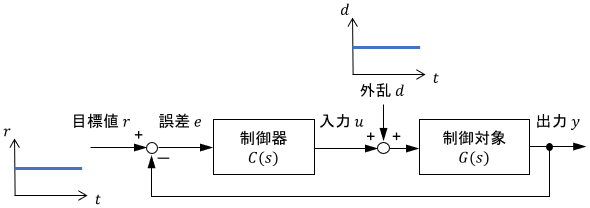

上のようなフィードバック制御システムにおいて、
- 制御器$C(s)$か制御対象$G(s)$のどちらかが積分要素$\frac{1}{s}$を持っていれば、ステップ目標値(一定の目標値)に対する定常偏差を0にできる
- 制御器$C(s)$が積分要素$\frac{1}{s}$を持っていれば、ステップ外乱(一定の外乱)の影響を0にできる
※本来内部モデル原理はステップ目標値・ステップ外乱以外に対しても適用できる理論ですが、実用上PID制御を使うときは「一定の外乱が作用する環境下でも、ある目標値に到達できるか」が重要となることがほとんどなので、これらステップ信号にフォーカスした説明をしています。内部モデル原理の詳細については、こちらのページをご覧ください。
Iの項を持つPID制御器・PI制御器は、次式のように通分すると積分要素を持つため、「上記条件を満たさない場合にIの項を付加することで、不足している積分要素を補える」と考えればOKです。
$$\begin{align}\mathrm{PID}制御器: & \quad K_P + \frac{K_I}{s} + K_Ds= \frac{K_D s^2+ K_P s + K_I}{\color{red}{s}}\\ \mathrm{PI}制御器: & \quad K_P + \frac{K_I}{s} \qquad \quad= \frac{K_P s + K_I}{\color{red}{s}}\qquad \color{red}{積分要素だ!}\end{align}$$
これらより、Iの項が必要となる条件は、次のようにまとめられます。
- 制御対象$G(s)$が積分要素を持っていない場合、定常偏差を0にするためにはIの項が必要
- システムに一定の外乱が作用する場合、その影響を0にするためにはIの項が必要
シミュレーション例で確認
ここからは、シミュレーション例にてP制御・PI制御・PD制御・PID制御を比較することで、上記イメージと理論が確かに成り立つことを確認していきましょう。
PID制御が必要な例
外乱がない場合
まずは、P・I・Dすべての項が必要となるような機械システムの例を見ていきましょう。上のイメージで言うと、「振動を抑制する要素が十分になく、目標値に留まることを邪魔する力が働く場合」ですね。
具体的には、次のようなシステムが挙げられます。
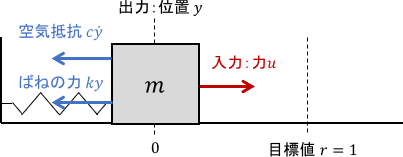

$m$は質点の質量、$u$は質点に加わる力、$y$は質点の位置、$k$はばね定数、$c$は粘性抵抗係数です。また、システム入力は力$u$、出力は位置$y$です。(以降の例でも同じです)
空気抵抗だけでは振動を十分に抑えられず、ばねの力が目標地点に留まることを邪魔するわけですね。
運動方程式より、このシステムの伝達関数は次のように求まります。
$$m\ddot{y} = -c\dot{y} – ky + u$$
$$Y(s) = \ubg{\frac{1}{ms^2+cs+k}}{伝達関数G(s)}U(s)$$
制御対象$G(s)$が積分要素$\frac{1}{s}$を持っていないので、内部モデル原理より「制御器にIの項がないと定常偏差が0にならない」ことが予想できます。
(さっきのやつ再掲)
- 制御対象$G(s)$が積分要素を持っていない場合、定常偏差を0にするためにはIの項が必要
- システムに一定の外乱が作用する場合、その影響を0にするためにはIの項が必要
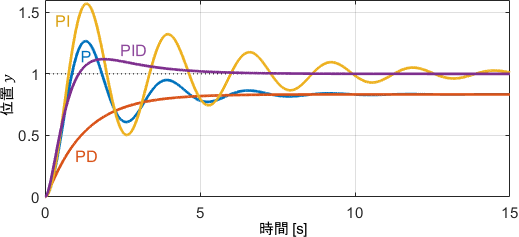
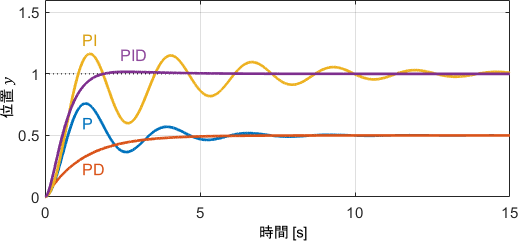
これらを確かめていきましょう。各種パラメータを適当に設定し、このシステムにそれぞれの制御器を適用した結果がこちらです。(※目標値は1です。以降も同様です)

| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | あり | あり |
| PD | なし | あり |
| PI | あり | なし |
| PID | なし | なし |
確かに、Dの項によって振動が無くなり、Iの項によって定常偏差が無くなっていることが分かります。
※今回は記事を簡潔にするために出力$y$のみを示していますが、制御結果の分析は入出力の両方を確認するのが基本です。制御結果の分析法については、こちらのページをご覧ください
外乱がある場合
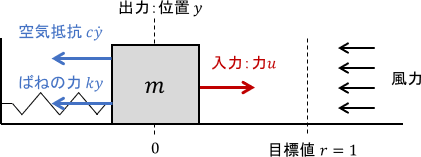
同じシステムに、一定の外乱として風力を作用させてみます。


| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | あり | あり(拡大) |
| PD | なし | あり(拡大) |
| PI | あり | なし |
| PID | なし | なし |
全体の傾向としては先ほどと同じですね。Iの項がない制御器では外乱によって定常偏差が拡大していますが、Iの項がある制御器では外乱下でも定常偏差をしっかり無くせていることが分かります。
これも内部モデル原理の結果と一致しますね。
PD制御でいい例(Iがいらない例)
外乱がない場合
続いて、Dの項は必要で、Iの項がいらない例を見てみましょう。上のイメージで言うと、「振動を抑制する要素が十分にないが、目標値に留まることを邪魔する力もない場合」ですね。
具体的には、次のようなシステムが挙げられます。
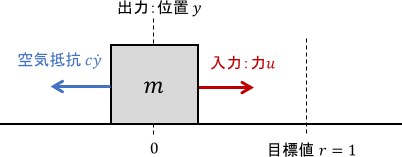

先ほどのシステムからばねが無くなり、目標値で邪魔する力が発生しなくなっています。
これが伝達関数にどのような影響を与えるかを見てみましょう。先ほどの式にて、$k=0$とすればOKですね。
$$G(s) = \frac{1}{ms^2+cs} = \frac{1}{\color{red}{s}(ms+c)}\quad\color{red}{積分要素だ!}$$
制御対象$G(s)$に積分要素$\frac{1}{s}$が現れるのがポイントです。直感的には、「対象システムが(ばねのように)目標値に留まることを邪魔する要素を持たなければ、伝達関数に積分要素が現れる」と解釈すればOKです。
積分要素を持つということは、内部モデル原理より「制御器にIの項がなくても定常偏差が0になる」ことが予想されますね。
(さっきのやつ再掲)
- 制御対象$G(s)$が積分要素を持っていない場合、定常偏差を0にするためにはIの項が必要
- システムに一定の外乱が作用する場合、その影響を0にするためにはIの項が必要
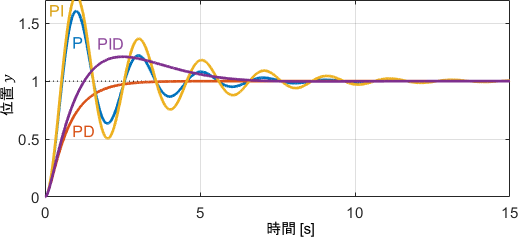
これらを確かめていきましょう。このシステムにそれぞれの制御器を適用した結果がこちらです。

| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | あり | なし |
| PD | なし | なし |
| PI | あり | なし |
| PID | なし | なし |
Dの項によって振動が抑えられているのは、前回と同じですね。
対して定常偏差に注目すると、予想通りI項の有無に関わらず定常偏差が無くなっていることが分かります。むしろ余分なI項(積分要素)を持つPI制御・PID制御は、P制御・PD制御よりも振動の幅が広がっており、安定性が低下していることが見て取れますね。
※積分要素と安定性の関係については、こちらのページをご覧ください
外乱がある場合
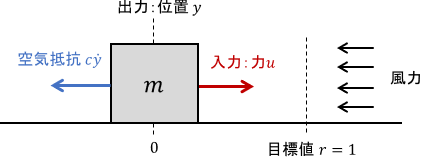
同じシステムに、一定の外乱として風力を作用させてみましょう。


| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | あり | あり |
| PD | なし | あり |
| PI | あり | なし |
| PID | なし | なし |
今度は、Iの項のないP制御・PD制御にて定常偏差が現れていますね。「外乱に対しては、制御対象ではなく制御器が積分要素を持つ必要がある」という内部モデル原理の結果と確かに一致しています。
Dの項と振動の関係は、先ほどと同じですね。
PI制御でいい例(Dがいらない例)
外乱がない場合
最後に、Iの項は必要で、Dの項がいらない例を見てみましょう。上のイメージで言うと、「振動を十分に抑制する要素があるが、目標値に留まることを邪魔する力が働く場合」ですね。
具体的には、次のようなシステムが挙げられます。
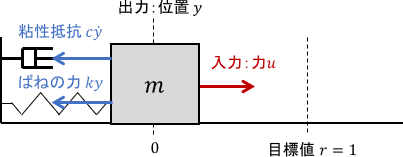

たまたまであれ、そう狙った設計であれ、何らかのダンピング作用によって振動が起きにくいシステム構造になっているイメージですね。目標地点では、ばねの力によってそこに留まることが邪魔されてしまいます。
システムの伝達関数は最初の例と同じですが、今回は粘性抵抗係数$c$がいい感じの値になっていると思えばOKです。
$$G(s) = \frac{1}{ms^2+cs+k}$$
制御対象$G(s)$が積分要素$\frac{1}{s}$を持っていないので、「制御器にIの項がないと定常偏差が0にならない」ことが予想されます。
このシステムにそれぞれの制御器を適用した結果がこちらです。
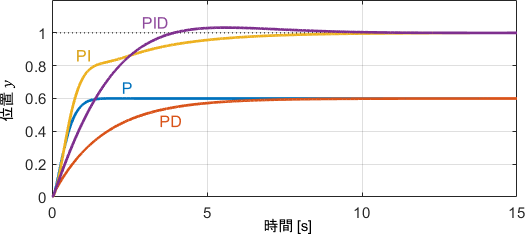

| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | なし | あり |
| PD | なし | あり |
| PI | なし | なし |
| PID | なし | なし |
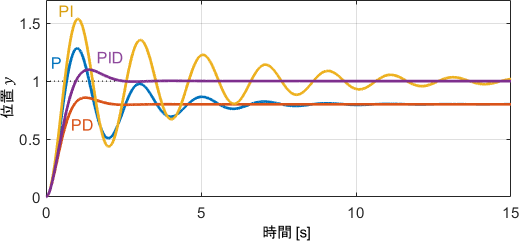
制御対象のもともとの性質から、Dの項の有無に関わらず振動が起きていないことが分かります。むしろ余分なD項を持つPD制御・PID制御は、P制御・PI制御よりも立ち上がりが遅くなっていることが見て取れます。
定常偏差は、予想通りIの項があれば0になっていますね。
外乱がある場合
これまでと同じように、風力を作用させてみます。
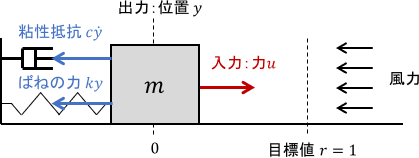

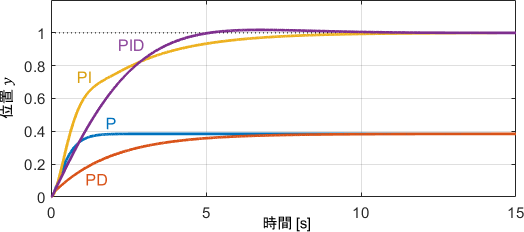

| 制御器 | 振動 | 定常偏差 |
|---|---|---|
| P | なし | あり(拡大) |
| PD | なし | あり(拡大) |
| PI | なし | なし |
| PID | なし | なし |
特に新しい観点はありません。Dの項による作用はそのままに、Iの項がない制御器では外乱によって定常偏差が拡大していますが、Iの項がある制御器では定常偏差が無くなっています。
以上、PI制御・PD制御・PID制御の違いと選び方でした。
制御器が適切に選択できれば、その後のPIDゲインチューニングによって良好な制御性能が得られやすくなります。PIDゲインチューニングについては、こちらのページにて具体的な方法を詳しく説明していますので、合わせてご覧ください。
- Pの項を基本として、必要に応じてI・Dの項を追加していけば必要な制御器が出来上がる
- Dの項が必要になるのは、システムに振動を抑制する要素が十分にない場合
- Iの項が必要になるのは、出力が目標値に留まるのを邪魔する何らかの作用が働く場合
- 余分な項を入れると制御性能が悪化しがちなので注意する








コメント