このページでは、システムの定常特性とその計算方法について、具体例を交えながら説明します。特に、フィードバック制御システムの定常偏差と内部モデル原理について詳しく解説します。
- フィードバック制御システムが目標値と同じ数の積分要素を持っていれば、定常偏差が0になる
- これを内部モデル原理と呼ぶ
- ただし、システムの積分要素が増えるほど安定性に悪影響が出るので注意が必要
- 積分要素が足りなくても、制御ゲインを大きくすれば定常偏差を低減できる
定常特性の概要
定常特性と定常偏差
システムが動作してから十分に時間がたち、定常状態に落ち着いたときの特性を、システムの定常特性と呼びます。(逆に定常状態に落ち着くまでの特性は、過渡特性と呼ばれます。)
定常特性にも色々ありますが、フィードバック制御システムにとっては「制御量が目標値に誤差なく追従できているかどうか」が非常に重要となります。この定常状態における誤差は、定常偏差と呼ばれます。
定常特性・定常偏差は、システムの数式モデル(伝達関数)を解けば計算できますが、当然システムが複雑になるほど計算が面倒になってしまいます…。
ただ古典制御では、ラプラス変換の便利な性質(最終値定理)を用いることで、システムの数式モデルを直接解くことなく定常特性を計算することが可能です。
以降、定常特性でも特に重要な「フィードバック制御システムの定常偏差」にフォーカスして、その特性と分析方法を詳しく見ていきましょう。
※定常特性を議論する際、対象とするシステムは安定であることが前提となります。安定でないと、そもそもシステムが定常状態に落ち着かないためです。安定性についての詳細は、こちらのページをご覧ください
目標値の種類
フィードバックシステムの定常偏差を評価する場合、目標値の基本単位として、ステップ目標値・ランプ目標値・加速度目標値を考えることがほとんどです。
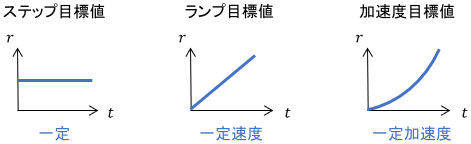
特にステップ目標値は、実用シーンで非常に多く用いられる、基本中の基本となる目標値です。
※加速度目標値は「パラボラ目標値」とも呼ばれます。英語では「パラボラ目標値」が正式名ですが、日本ではあまりメジャーな呼び方でないため、本ページでは「加速度目標値」を用います。
以降の数式表現をスッキリさせるため、本ページでは各種係数を1に統一した「単位目標値」を使用することにします。それぞれの数式表現$r(t)$と、そのラプラス変換$R(s)$を次に示します。
$$\begin{array}{lll} 単位ステップ目標値 & r(t)=1 & R(s) = \frac{1}{s} \\[2pt] 単位ランプ目標値 & r(t) = t & R(s) = \frac{1}{s^2} \\ 単位加速度目標値 & r(t) = \frac{t^2}{2} & R(s) = \frac{1}{s^3}\end{array}$$
「単位」でない目標値は単位目標値の組み合わせで表現できるので、結局単位目標値に対する特性を調べればOK、ということになります。

定常偏差の計算
それでは、それぞれの目標値に対する定常偏差を実際に計算し、その特性を深掘りしていきましょう。
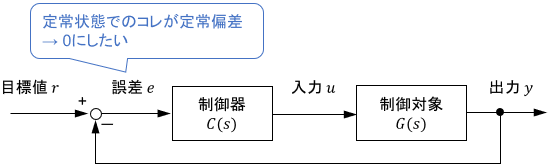
ここでは、次のブロック線図で表されるフィードバック制御システムを考えます。

$C(s)$は制御器の伝達関数、$G(s)$は制御対象の伝達関数です。
最終値定理を用いた導出
定常偏差$e_s$を数式で表すと、次のようになりますね。
$$e_s = \lim _{t\rightarrow \infty} e(t)$$
これを直接計算してもよいのですが、ラプラス変換の最終値定理を用いると、上式を$s$領域にて計算することができます。つまり、伝達関数表現のまま$e_s$が計算できるので、面倒な逆ラプラス変換なしにお手軽に分析が可能となります。
$$最終値定理:\lim _{t\rightarrow \infty} f(t) = \lim _{s\rightarrow 0} s F(s)$$
$F(s)$は$f(t)$のラプラス変換です。元の関数$f(t)$のラプラス変換$F(s)$に$s$をかけて、$t\rightarrow \infty$の代わりに$s \rightarrow 0$とすれば、同じ解が得られるというわけですね。
※ラプラス変換の基礎については、こちらのページをご覧ください
これを用いて先ほどの定常偏差を計算すると、次式が得られます。
$$e_s = \lim _{t\rightarrow \infty} e(t) = \lim _{s\rightarrow 0} sE(s)$$
$E(s)$は誤差$e(t)$のラプラス変換です。
では、中身の$E(s)$を計算していきましょう。ブロック線図上の関係性より、$E(s)$は次のように求められます。

$$\begin{align}ブロック線図より、 & E(s) = R(s) – Y(s)\\[8pt] Y(s)をE(s)で表して、\ & E(s) = R(s) – C(s)G(s)E(s)\\[3pt] E(s)で整理して、\ & E(s) = \frac{1}{1 + C(s)G(s)} \cdot R(s) \end{align}$$
$R(s)$は目標値$r(t)$のラプラス変換、$Y(s)$は出力$y(t)$のラプラス変換です。これを先ほどの式に代入すると、定常偏差$e_s$の計算式が求まります。
$$e_s = \lim _{s\rightarrow 0} sE(s) = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)}\cdot R(s)$$
この式を用いて、各種目標値に対する定常偏差を計算していきましょう。
単位ステップ目標値に対する定常偏差
目標値として、単位ステップ目標値$R(s)=\frac{1}{s}$を与えた場合を考えます。

このときのシステムの定常偏差$e_s$は、次のように計算できます。
$$e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)} \cdot \ubgd{\frac{1}{s}}{ステップ}{目標値} = \lim _{s\rightarrow 0} \frac{1}{1 + C(s)G(s)} $$
最終値定理によってかけられた$s$が、ちょうどステップ目標値$\frac{1}{s}$に打ち消されていますね。
制御の目的としては$e_s=0$を目指したいわけですが、そのためには開ループ伝達関数$C(s)G(s)$が$s\rightarrow 0$で$\infty$になればよいことになります。
$$e_s = \lim _{s\rightarrow 0} \frac{1}{1 + \ubg{C(s)G(s)}{\inftyになればe_s=0}} $$
では、どんなときにこれが満たされるのでしょうか。結論を言うと、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を1個(以上)持てばOK、ということになります。
$$C(s)G(s) = \ubg{\frac{1}{s}}{\inftyになる} \cdot \ubgd{L(s)\vphantom{\frac{1}{s}}}{その他}{の部分}$$
積分要素が$s\rightarrow 0$で$\infty$に発散してくれるというわけですね。「ステップ目標値$\frac{1}{s}$に対しては、$\frac{1}{s}$があればOK」と頭に入れて、次に行きましょう。
※$C(s)G(s)$は既約形式である(限界まで約分してある)ことが前提です。例えば$\frac{1}{s}\cdot\frac{s}{s+1}$は一見積分要素を持ってそうですが、約分すると$\frac{1}{s+1}$なので実際は持っていません。
※ちなみに、システムが積分要素を持つことを「積分器を持つ」と言ったりもします
単位ランプ目標値に対する定常偏差
目標値として、単位ランプ目標値$R(s)=\frac{1}{s^2}$を与えた場合を考えましょう。

このときの定常偏差$e_s$も、同様に計算していきます。
$$e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)} \cdot \ubgd{\frac{1}{s^2}}{ランプ}{目標値} = \lim _{s\rightarrow 0} \frac{1}{s + sC(s)G(s)} $$
先ほどより分母の$s$の次数が1大きくなっていますね。$e_s=0$とするためには、$sC(s)G(s)$が$s\rightarrow 0$で$\infty$になればよいことになります。
$$e_s = \lim _{s\rightarrow 0} \frac{1}{\ubg{s}{0になる} + \ubg{sC(s)G(s)}{\inftyになればe_s=0}} $$
先ほどと同様に考えると、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を2個(以上)持てばOKですね。
$$C(s)G(s) = \ubgd{\frac{1}{s}}{前のsを}{打ち消す}\cdot \obg{\frac{1}{s}}{\inftyになる} \cdot \ubgd{L(s)\vphantom{\frac{1}{s}}}{その他}{の部分}$$
1個目の積分要素が前についた$s$を打ち消し、2個目の積分要素が$s\rightarrow 0$で$\infty$に発散してくれるというわけですね。「ランプ目標値$\frac{1}{s^2}$に対しては、$\frac{1}{s^2}$があればOK」と頭に入れて、次に行きましょう。
単位加速度目標値に対する定常偏差
最後に、目標値として単位加速度目標値$R(s)=\frac{1}{s^3}$を与えた場合を考えましょう。

このときの定常偏差$e_s$を計算していきます。
$$e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)} \cdot \ubgd{\frac{1}{s^3}}{加速度}{目標値} = \lim _{s\rightarrow 0} \frac{1}{s^2 + s^2C(s)G(s)} $$
また分母の$s$の次数が1大きくなっていますね。$e_s=0$とするためには、$s^2C(s)G(s)$が$s\rightarrow 0$で$\infty$になればよいことになります。
$$e_s = \lim _{s\rightarrow 0} \frac{1}{\ubg{s^2}{0になる} + \ubg{s^2C(s)G(s)}{\inftyになればe_s=0}} $$
だいたい分かってきたと思いますが、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を3個(以上)持てばOKですね。
$$C(s)G(s) = \ubgd{\frac{1}{s^2}}{前のs^2を}{打ち消す}\cdot \obg{\frac{1}{s}}{\inftyになる} \cdot \ubgd{L(s)\vphantom{\frac{1}{s}}}{その他}{の部分}$$
「加速度目標値$\frac{1}{s^3}$に対しては、$\frac{1}{s^3}$があればOK」と頭に入れて、次に行きましょう。
内部モデル原理
ここまでステップ目標値・ランプ目標値・加速度目標値に対する定常偏差を見てきましたが、同様の議論により、より高次の目標値に対しても同じ法則が成り立ちます。
- $R(s)=\frac{1}{s}$に対しては、$C(s)G(s)$が$\frac{1}{s}$を持てば定常偏差が0になる
- $R(s)=\frac{1}{s^2}$に対しては、$C(s)G(s)$が$\frac{1}{s^2}$を持てば定常偏差が0になる
- $R(s)=\frac{1}{s^3}$に対しては、$C(s)G(s)$が$\frac{1}{s^3}$を持てば定常偏差が0になる
- $R(s)=\frac{1}{s^k}$に対しては、$C(s)G(s)$が$\frac{1}{s^k}$を持てば定常偏差が0になる
上記より、定常偏差を0にするためには、開ループシステムが目標値と同じ数の積分要素を持っていればよいことが分かります。
この法則は、内部モデル原理と呼ばれます。覚えやすくていいですね!
シミュレーション例
問題設定
それでは、内部モデル原理が本当に成り立つのか、実際にシミュレーションしてみましょう。
例題として、次のシステムを考えます。
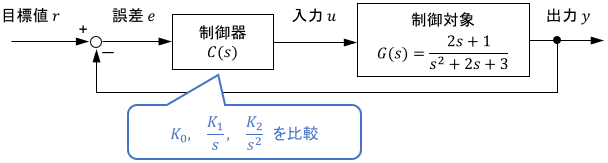
制御対象$G(s)=\frac{2s+1}{s^2+2s+3}$は積分要素を1個も持っていないことに注意してください。これに対して、次のような制御器$C(s)$で積分要素をいくつか付加していき、定常偏差を比較しましょう。
$$\begin{array}{lll} C(s) = K_0 & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{0}}個 \\[5pt] C(s) = \frac{K_1}{s} & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{1}}個 \\[5pt] C(s) = \frac{K_2}{s^2} & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{2}}個\end{array}$$
$K_0, K_1, K_2$は、定数の制御ゲイン(調整パラメータ)です。
※今回は分かりやすさのために制御器$C(s)$を積分要素だけで構成していますが、実用シーンではこのようなことはせず、積分要素を他の要素と組み合わせて使用することがほとんどです。積分要素の実用法については、こちらのページをご覧ください。
ステップ目標値に対するシミュレーション
まず、単位ステップ目標値$R(s)=\frac{1}{s}$を用いてシミュレーションしてみましょう。
ステップ目標値$R(s)=\frac{1}{s}$に対しては、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を1個(以上)持てばOKでしたね。これを確かめてみましょう。
適当な$K_0, K_1, K_2$を用いてシミュレーションした結果がこちらです。
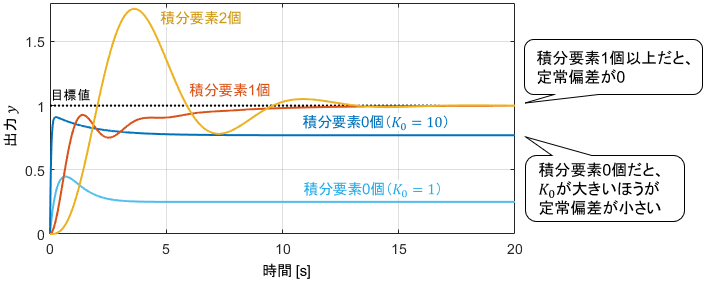
確かに、積分要素を1個以上持っている場合に定常偏差が0となっていますね。
対して、積分要素が0個の場合は一定の定常偏差が残ってしまっています。さらに観察すると、制御ゲイン$K_0$が大きいほうが定常偏差が小さくなっていますね。
これについて、数式で確認してみましょう。各制御器に対する定常偏差$e_s$を計算すると、次のようになります。(計算結果だけ見ればOKです)
$$e_s =\lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)} \cdot R(s) \quad より、$$
$$\begin{alignat}{3} &C(s) = K_0\text{のとき} &&\qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + K_0\frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s} = \frac{1}{1 + \frac{K_0}{3}}&&\quad\color{green}{確かに一定!}\\[7pt] &C(s) = \frac{K_1}{s}\text{のとき} &&\qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + \frac{K_1}{s}\cdot\frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s} = 0 && \quad \color{green}{確かに0!}\\[7pt] &C(s) = \frac{K_2}{s^2}\text{のとき} && \qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + \frac{K_2}{s^2}\cdot \frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s} = 0&& \quad \color{green}{確かに0!}\end{alignat}$$
$C(s)=K_0$、つまり積分要素が0個の場合は、制御ゲイン$K_0$が大きくなればなるほど$e_s$の分母が大きくなるため、結果的に定常偏差が小さくなることが分かりますね。
よって、 積分要素が足りない場合は、制御ゲインをなるべく大きくすれば定常偏差を低減できることが分かります。
※ただし制御ゲインを上げれば上げるほど入力飽和(システムの能力以上の要求を出してしまうこと)のリスクが高まります。極端な話、$K_0=\infty$を入れてもシステムはそれを実現できませんので、システムの能力の範囲内でゲインを調整する必要があることに注意してください。
ランプ目標値に対するシミュレーション
次に、単位ランプ目標値$R(s)=\frac{1}{s^2}$を与えてシミュレーションしてみます。
ランプ目標値$\frac{1}{s^2}$に対しては、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を2個(以上)持てばOKでしたね。
適当な$K_0, K_1, K_2$を用いてシミュレーションした結果がこちらです。
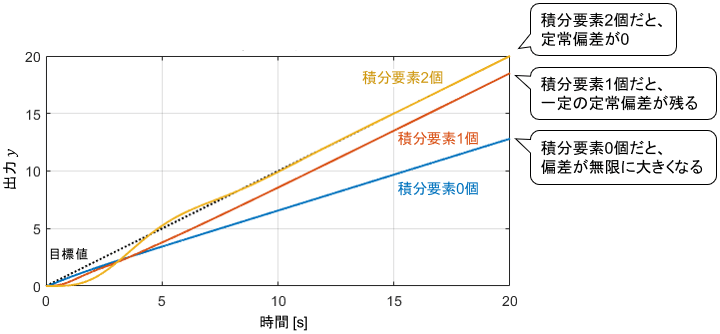
確かに、積分要素を2個持っている場合に定常偏差が0となっていますね。
対して、積分要素が1個の場合は一定の定常偏差が残ってしまい、0個の場合は偏差が時間とともに無限に大きくなってしまっています。
これも数式で確認してみましょう。各制御器に対する定常偏差$e_s$を計算すると、次のようになります。(これも計算結果だけ見ればOKです)
$$e_s =\lim _{s\rightarrow 0} s \cdot \frac{1}{1 + C(s)G(s)} \cdot R(s) \quad より、$$
$$\begin{alignat}{3} &C(s) = K_0のとき &&\qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + K_0\frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s^2} = \infty &&\quad\color{green}{確かに\infty!}\\[7pt] &C(s) = \frac{K_1}{s}のとき &&\qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + \frac{K_1}{s}\cdot\frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s^2} = \frac{1}{1 + \frac{K_1}{3}} &&\quad \color{green}{確かに一定!}\\[7pt] &C(s) = \frac{K_2}{s^2}のとき &&\qquad e_s = \lim _{s\rightarrow 0} s \cdot \frac{1}{1 + \frac{K_2}{s^2}\cdot \frac{2s+1}{s^2+2s+3}} \cdot \frac{1}{s^2} = 0&& \quad\color{green}{確かに0!}\end{alignat}$$
確かに計算結果がシミュレーションと一致していますね。$C(s) = \frac{K_1}{s}$、つまり積分要素が1個の場合は、先ほどと同じ理屈で制御ゲイン$K_1$が大きくなればなるほど定常偏差が小さくなることも分かります。
加速度目標値に対するシミュレーション
最後に、単位加速度目標値$R(s)=\frac{1}{s^3}$を与えてシミュレーションしてみます。
加速度目標値$\frac{1}{s^3}$に対しては、開ループ伝達関数$C(s)G(s)$が積分要素$\frac{1}{s}$を3個(以上)持てばOKでしたね。
適当な$K_0, K_1, K_2$を用いてシミュレーションした結果がこちらです。
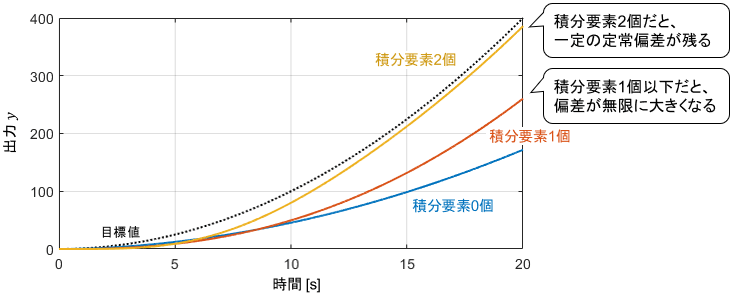
これまでの傾向通り、積分要素が2個の場合は一定の定常偏差が残り、1個以下の場合は偏差が時間とともに無限に大きくなっていますね。
では積分要素が3個なら定常偏差がなくなるかというと、そうはなりません(あくまで今回の場合は)。積分要素3個の場合のシミュレーション結果がこちらです。

それどころか、出力がどんどん大きくなり、発散してしまっていますね…。なぜ内部モデル原理が成り立たないのでしょうか。この理由について、説明していきましょう。
安定性と実用上のポイント
上記シミュレーションが発散してしまった理由は、積分要素を加えすぎてシステムが不安定になったからです。(逆に言うと、システムの安定性が保たれていれば、定常偏差はちゃんとなくなります)
定常特性を議論する際は、システムが安定であることが大前提となっていました。内部モデル原理や最終値定理もシステムが安定であることを前提とした理論であるため、これが崩れてしまうと数式上の計算は意味をなさなくなってしまいます。

…なんで積分要素を加えるとシステムの安定性が崩れるの?
積分要素$\frac{1}{s}$の極は0なので、積分要素単体は安定なシステムではありません。よって、これを付ければ付けるほどシステム全体の安定性がどんどん悪くなる、というのがざっくりとしたイメージです。

※積分要素と安定性の詳細については、こちらのページをご覧ください

…じゃあいくつまでなら付けていいの?
これに関しては、システムの安定余裕次第なので、システムに応じてケースバイケースで判断する必要があります。
※安定余裕の詳細については、こちらのページをご覧ください
とはいえ、実用上は積分要素は2個以下しか使われないことがほとんどです。通常は0個、それだと定常偏差が大きすぎるなら1個、どうしても必要な特別な理由があれば2個、といったイメージを持っておけばよいでしょう。

え、でも積分要素が少ないと定常偏差が出ちゃうんじゃないの?
その通りです。ただ前述の通り、定常偏差は制御ゲインを大きくすることによって、低減させることが可能です。ゲインの調整によって実用上問題ない精度が実現できるのであれば、わざわざ安定性を脅かす積分要素を追加する必要はないというわけですね。

内部モデル原理は、あくまで定常偏差を厳密に0にするための条件であることに注意してくださいね。
以上、システムの定常特性と内部モデル原理についての解説でした。
内部モデル原理は、システムに外乱が加わる場合にも有効であることが知られています。それについては、こちらの記事で詳しく解説していますので、合わせてご覧ください。
- フィードバック制御システムが目標値と同じ数の積分要素を持っていれば、定常偏差が0になる
- これを内部モデル原理と呼ぶ
- ただし、システムの積分要素が増えるほど安定性に悪影響が出るので注意が必要
- 積分要素が足りなくても、制御ゲインを大きくすれば定常偏差を低減できる








コメント