このページでは、制御を考える上で非常に重要な、システムの安定性について解説します。特に、数式上の定義ではなく「安定であるとは結局なんなのか」というイメージについて詳しく説明します。
- 安定なシステムは、何も入力せずにほっといたら(ほぼ)止まる
- 不安定なシステムは、何も入力せずにほっといたら暴走する
- 安定性には色々な種類があるが、本質的にはだいたい同じと考えてOK
安定性の直感的意味
安定なシステム
安定なシステムとは「何も入力せずにほっといても、出力や状態が発散しないシステム」のことです。
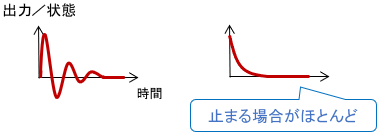
現実のシステムはほとんどの場合「停止」という状態に収束するので、少し乱暴ですが直感的には「何もせずにほっといたら、止まるシステム」とイメージしても大丈夫です。
※システムは最初に平衡状態(収束先の状態)には無いとします。例えば「止まっているシステムをほっといたら止まったままだ!」というケースは考えません。以降、「システムが動作をしている途中でほっとく」イメージで読み進めてください。
不安定なシステム
不安定なシステムとは「何も入力せずにほっといたら、出力や状態が発散するシステム」のことです。
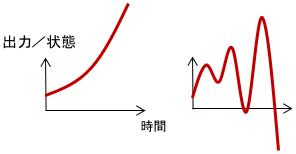
直感的には「何もせずにほっといたら、暴走するシステム」と考えると分かりやすいと思います。
それぞれの例を見ていきましょう。
安定なシステムの例
振り子
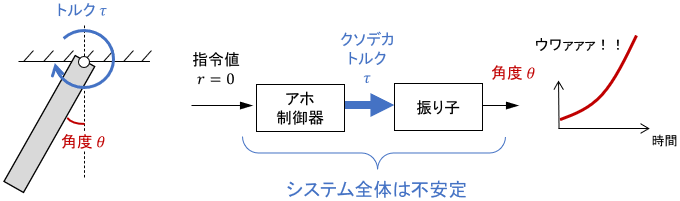
振り子はほっといたら摩擦で止まるので、安定なシステムです。
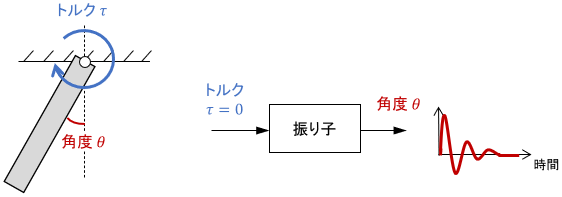
振り子に限らず、ほとんどの機械システムは単体では安定です。だいたいほっといたら止まりますからね。(不安定な例は後で紹介します)
電気回路
RLC回路のような単純な回路も、スイッチを切れば(=入力を与えなければ)止まるので、安定ですね。

機械システムと同じく、電気システムも単体ではほとんどが安定です。スイッチを切ると止まりますからね。
不安定なシステムの例
ドローン
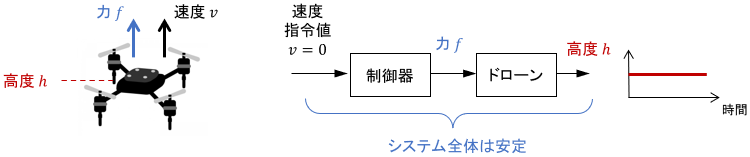
ドローンは何もせずにほっといたら落ちるので、不安定なシステムです。
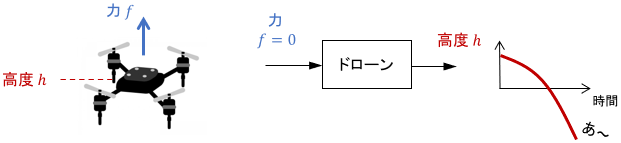
地面がないと無限に落ち続けるので、状態が収束しません。
マイクのハウリング
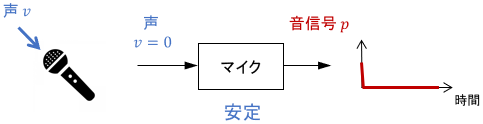
スピーカーの音をマイクが拾うと、音が無限に増幅されてハウリングしますよね。
何も声を出さなくても(=入力を与えなくても)ハウリングは収まりませんので、不安定なシステムです。

安定性を考えるときの注意点
安定性は「見ているシステムの範囲」によって変わってくるので注意が必要です。
例えば先ほどのドローンは、単体では不安定なシステムでしたが、適切に制御器を設計できれば制御システム全体を安定化できます。
また、マイクのハウリングはシステム全体は不安定でしたが、マイク単体は安定なシステムです。
振り子も単体では安定でしたが、アホ制御器に繋げば簡単に不安定になります。
以上の通り、安定性を考える時は「今自分がどの範囲を見ているのか」を常に意識してくださいね。
安定性にも色々な種類がある
実は、制御工学における安定性には色々な種類があります。
基本的なイメージとしては、上記の通り「暴走しなければ安定」と考えて問題ありません。ただし、どこまでを「暴走」とみなすかによって細かい定義が変わってきます。順番に見ていきましょう。
インパルス応答に基づく安定性
「インパルス入力を与えてほっといたら、出力や状態が0に収束するかどうか」を指標とした安定性です。
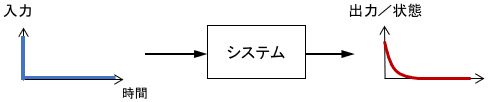
インパルス応答は「最初に一瞬ガンッ!と大きな入力を与えて平衡状態を乱し、あとは何もせずほっといたらどうなるか」を表したものなので、これまで考えてきたものと同じイメージの安定性ですね。
※インパルス応答の詳細については、こちらのページをご覧ください
ステップ応答に基づく安定性
「ステップ入力を与えてほっといたら、出力や状態が何らかの定常状態に落ち着くかどうか」を指標とした安定性です。
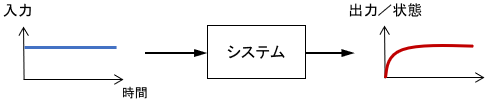
インパルス応答と異なり常に入力があるので、「停止」という状態に収束することは少ないです。「ステップ入力に対して発散しなければOK」と考えればよいでしょう。
※ステップ応答の詳細については、こちらのページをご覧ください
有界入出力安定性
「有界な入力に対して、出力も有界であるかどうか」を指標とした安定性を、有界入出力安定性と呼びます(Bounded-Input-Bounded-Output安定性、略してBIBO安定性とも呼ばれます)。
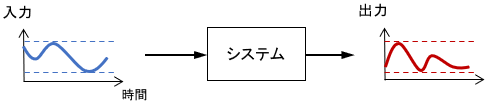
簡単に言うと、「無限じゃない入力に対して、出力も無限に吹っ飛ばないならOK」という安定性ですね。
以上、3つの安定性を紹介してきましたが、プロパーなシステムに対しては、これら3つの安定性が等価であることが知られています。なので「安定性は色々あるけど、ほとんどの場合は実質同じ」と考えてOKです。
※「プロパーなシステム」を超ざっくり説明すると、「制御工学の教科書にでてくるような基本的なシステム」のことです。詳細はこちらのページで解説しています。
以上、システムの安定性の意味と直感的イメージについての解説でした。
こちらのページではシステムの安定性を判別する方法を解説していますので、合わせてご覧ください!
- 安定なシステムは、何も入力せずにほっといたら(ほぼ)止まる
- 不安定なシステムは、何も入力せずにほっといたら暴走する
- 安定性には色々な種類があるが、本質的にはだいたい同じと考えてOK







コメント