このページでは、フィードバック制御システムに外乱が加わる場合の定常偏差と内部モデル原理について、詳しく解説します。
※本ページは、こちらのページの続きです。定常偏差・内部モデル原理について未学習の方は、まずこちらのページをご覧ください
- フィードバック制御器が外乱と同じ数の積分要素を持っていれば、外乱の影響を0にできる
- つまり、外乱に対しても内部モデル原理が成り立つ
- 積分要素が足りなくても、制御ゲインを大きくすれば外乱の影響を低減できる
外乱に対する定常偏差の計算
最終値定理を用いた導出
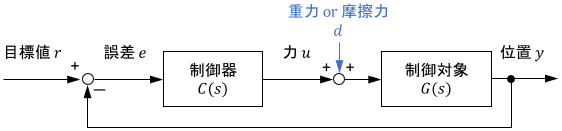
次のように、フィードバック制御システムに外乱が加わる場合を考えましょう。
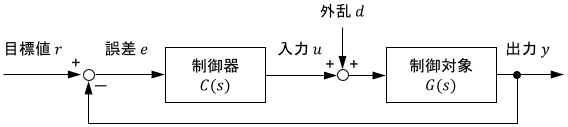

$C(s)$は制御器の伝達関数、$G(s)$は制御対象の伝達関数です。
この条件における定常偏差$e_s$を計算していきます。定常偏差は、ラプラス変換の最終値定理を用いて次式で計算できるのでしたね。
$$e_s = \lim _{t\rightarrow \infty} e(t) = \lim _{s\rightarrow 0} sE(s)$$
$E(s)$は誤差$e(t)$のラプラス変換です。$E(s)$は、ブロック線図上の関係より次のように求まります。
$$\begin{align}ブロック線図より、 & E(s) = R(s) – Y(s)\\[8pt] Y(s)をE(s),D(s)で表して、\ & E(s) = R(s) – G(s)\bigr\{C(s)E(s)+D(s)\bigl\}\\[3pt] E(s)で整理して、\ & E(s) = \ubg{\frac{1}{1 + C(s)G(s)} R(s)}{前回と同じもの} – \ubg{\frac{G(s)}{1+C(s)G(s)}D(s)}{外乱の影響} \end{align}$$
$R(s)$は目標値$r(t)$のラプラス変換、$Y(s)$は出力$y(t)$のラプラス変換 、$D(s)$は外乱$d(s)$のラプラス変換です。目標値$R(s)$が作用する項は前回と全く同じです。それに加え、外乱$D(s)$が作用する項が増えていますね。
これを最終値定理の式に代入することで、定常偏差が次のように求まります。
$$e_s = \lim _{s\rightarrow 0} sE(s) = \lim _{s\rightarrow 0} \Biggl\{\ubg{s \cdot\frac{1}{1 + C(s)G(s)} R(s)}{前回と同じもの} – \ubg{s \cdot\frac{G(s)}{1+C(s)G(s)}D(s)}{外乱の影響}\Biggr\}$$
定常偏差が0になるには、$R(s)$の項に加えて、$D(s)$の項も0になる必要があるというわけですね。$R(s)$の項の考え方は前回と同じなので置いておいて、$D(s)$の項について考えていきましょう。
単位ステップ外乱に対する定常偏差
ステップ外乱$D(s)=\frac{1}{s}$が与えられた場合を考えます。

このとき、$D(s)$の項は次のようになりますね。
$$D(s)の項=\lim _{s\rightarrow 0}s \cdot\frac{G(s)}{1+C(s)G(s)}\cdot \ubgd{\frac{1}{s}}{ステップ}{外乱}=\lim _{s\rightarrow 0}\frac{G(s)}{1+C(s)G(s)}$$
よってこの項が0になるためには、$s\rightarrow 0$で$G(s)$が0になるか、$C(s)$が$\infty$になればよいことになります。
$$D(s)の項=\lim _{s\rightarrow 0}\frac{\obg{G(s)}{これが0か}}{1+\ubg{C(s)}{これが\infty}G(s)}$$
※$G(s)$だけが$\infty$になると、$\frac{1}{C(0)}$に収束してしまうことに注意してください
そしてこれが満たされるためには、制御対象$G(s)$が微分要素$s$を持つか、制御器$C(s)$が積分要素$\frac{1}{s}$を持てばよいことになりますね。
古典制御で取り扱うプロパーなシステムが微分要素を持つことはまずないため、実用上は制御器 $C(s)$ が積分要素を持っているかどうかが重要となります。
※プロパーなシステムと微分要素の関係性については、こちらのページをご覧ください。
結局、「ステップ外乱$\frac{1}{s}$に対しては制御器$C(s)$が$\frac{1}{s}$を持てばOK」と、前回と同じような結果が得られました。
ランプ外乱・加速度外乱に対しても、同様の議論により同様の結果が得られます(余裕のある方は計算してみてください)。

すなわち、外乱に対しても内部モデル原理が同様に成り立つというわけですね。
内部モデル原理のまとめ
前回と今回の議論を統合すると、内部モデル原理は次のようにまとめられます。


- 目標値$R(s)=\frac{1}{s^k}$に対しては、$C(s)G(s)$が$\frac{1}{s^k}$を持てば定常偏差が0になる
- 外乱$D(s)=\frac{1}{s^k}$がある場合は、$C(s)$が$\frac{1}{s^k}$を持てばその影響が0になる
目標値に対しては$C(s)G(s)$が対象ですが、外乱に対しては$C(s)$単体が対象になることに注意してください。つまり、制御対象$G(s)$がもともと積分要素を持っている場合は、制御器$C(s)$が持つべき積分器の数がそれぞれで異なることになります。
結局、制御器$C(s)$に積分要素を持たせれば間違いはないのですが、積分要素を増やすとシステムの安定性が低下することも、思い出しておきましょう。
※積分要素と安定性の詳細については、こちらのページをご覧ください
シミュレーション例
それでは、上記が本当に成り立つのかどうかをシミュレーションにて確認してみましょう。
例題として、ステップ目標値$R(s)=\frac{1}{s}$と ステップ外乱$D(s)=\frac{1}{s}$を与えられた次のシステムを考えます。
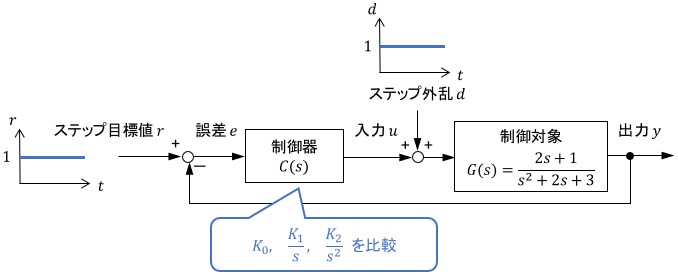

制御対象$G(s)=\frac{2s+1}{s^2+2s+3}$は積分要素を1個も持っていないことに注意してください。これに対して、次のような制御器$C(s)$で積分要素をいくつか付加していき、定常偏差を比較しましょう。
$$\begin{array}{lll} C(s) = K_0 & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{0}}個 \\[5pt] C(s) = \frac{K_1}{s} & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{1}}個 \\[5pt] C(s) = \frac{K_2}{s^2} & のとき & C(s)G(s)は積分要素\color{red}{\mathbf{2}}個\end{array}$$
$K_0, K_1, K_2$は、定数の制御ゲイン(調整パラメータ)です。これらを適当な値に設定してシミュレーションした結果がこちらです。
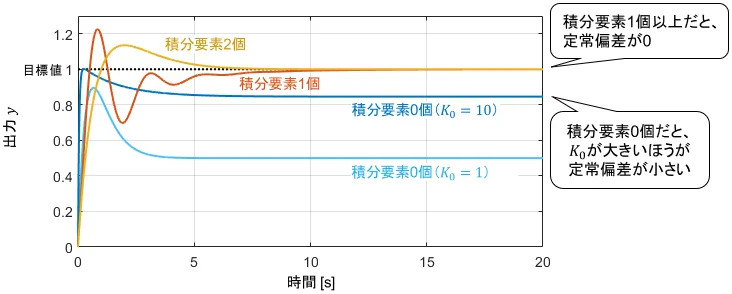

内部モデル原理の通り、制御器$C(s)$が積分要素を1個以上持つ場合に外乱の影響が打ち消され、定常偏差が0になっていますね。
対して、積分要素が0個の場合は一定の定常偏差が残ってしまっています。さらに観察すると、制御ゲイン$K_0$が大きいほうが定常偏差が小さくなっていますね。
これについて、数式で確認してみましょう。制御器$C(s)=K_0$に対する定常偏差$e_s$を計算すると、次のようになります。 (計算結果だけ見ればOKです)
$$e_s = \lim _{s\rightarrow 0} \Biggl\{s \cdot\frac{1}{1 + C(s)G(s)} R(s) – s \cdot\frac{G(s)}{1+C(s)G(s)}D(s)\Biggr\}\quad より、C(s)=K_0のとき、$$
$$ e_s = \lim _{s\rightarrow 0} \Biggl\{\ubg{s \cdot\frac{1}{1 + K_0\frac{2s+1}{s^2+2s+3} } \cdot \frac{1}{s}}{R(s)の項}\ -\ \ubg{s \cdot\frac{ \frac{2s+1}{s^2+2s+3} }{1+ K_0\frac{2s+1}{s^2+2s+3} } \cdot \frac{1}{s}}{D(s)の項} \Biggr\} = \ubg{\frac{1}{1 + \frac{K_0}{3} }}{R(s)の項}+\ubg{\frac{\frac{1}{3}}{1+\frac{K_0}{3}}}{D(s)の項}$$
$R(s)$の項、$D(s)$の項ともに、制御ゲイン$K_0$が大きくなればなるほど分母が大きくなるため、結果的に定常偏差が小さくなることが数式からも分かりますね。
よって外乱がある条件でも、 積分要素が足りない場合は、制御ゲインをなるべく大きくすればその影響を低減できることが分かります。
外乱に関する実用上のポイント
ステップ以外の外乱はほとんど使われない
上の方で、「ランプ外乱・加速度外乱に対しても、内部モデル原理に基づいて積分要素を付加すればその影響を0にできる」と説明しました。
もちろんこれは正しいのですが、実用上はステップ外乱を取り扱うことがほとんどでしょう。ランプ外乱・加速度外乱は時間とともに無限に増えていきますが、そのような外乱は現実にはほぼありませんからね。
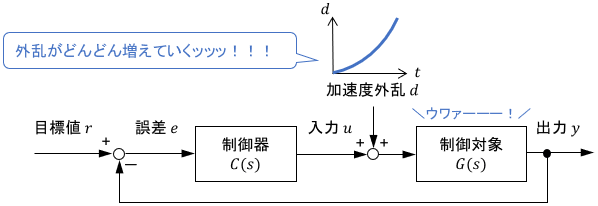

ステップ外乱のイメージと例


その「ステップ外乱」って具体的にどんなもの?
これは、システムに常に加わる一定の作用をイメージすればOKです。例えば機械システムであれば、システムに常に加わる重力や摩擦力のイメージですね。
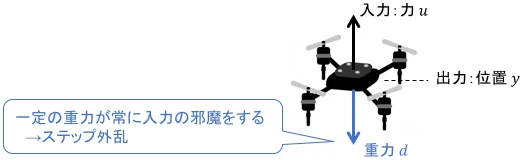

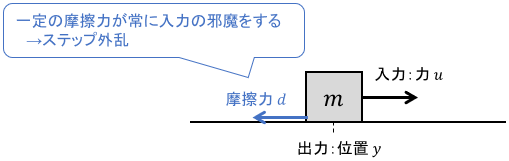

これらの力は、ブロック線図上でもちょうど入力に足し合わせる形で(外乱として)作用することになります。

これらの例のように原因が明確でなくても、様々な作用によって結果的に生じる「入力のズレ」をステップ外乱で表すこともよくあります。
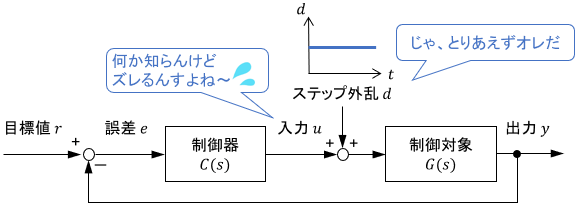

「原因が何であれ、入力に生じる一定のズレは、積分要素を1つ付加しておけばその影響を0にできる」と考えれば、内部モデル原理の便利さがよく分かるのではないでしょうか。
以上、フィードバック制御システムに外乱が加わる場合の、定常偏差と内部モデル原理についての解説でした。
本ページでは「積分要素がなぜ外乱の影響を打ち消すのか」を数式に基づいて説明しましたが、こちらのページではそれを直感的なイメージに基づいて説明していますので、合わせてご覧ください。(PID制御のI項の説明部分です)
- フィードバック制御器が外乱と同じ数の積分要素を持っていれば、外乱の影響を0にできる
- つまり、外乱に対しても内部モデル原理が成り立つ
- 積分要素が足りなくても、制御ゲインを大きくすれば外乱の影響を低減できる







コメント