このページでは、高次系の伝達関数と直感的イメージについて解説します。また、2次遅れ要素がなぜ伝達関数の基本要素に含まれるのかについても解説します。
- 高次系のほとんどは、伝達関数の基本要素の組み合わせで表現できる
- ある要素の出力が他の要素の入力になっている場合は、それぞれの要素をつなぐだけで全体の(高次の)伝達関数が作れる
- そうでない場合は、微分方程式を整理して伝達関数を導く
- 高次系の極は、それを構成する各基本要素の極に等しい
高次系とは?
3次以上のシステム、つまり特性が3階以上の微分方程式で表されるシステムは高次系(高次システム)と呼ばれます。高次系は、シンプルなシステムを複数組み合わせた形をしていることが多いです。
また、高次系のほとんどは、伝達関数の基本要素(1次遅れ要素・2次遅れ要素・積分要素・比例要素など)の組み合わせで表現できることが知られています。
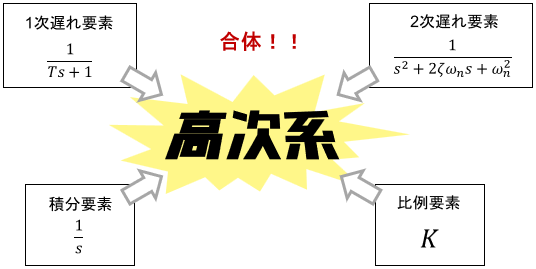
※伝達関数の基本要素については、こちらのページをご覧ください
以降、具体例でこの意味を見ていきましょう。
シンプルな例でイメージを把握!
高次系のイメージ
下図のように、プロペラの風で力を発生させ、台車を動かすシステムを考えます。
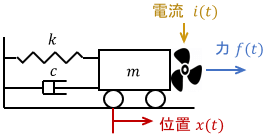
プロペラは、入力電流$i(t)$に応じて風力$f(t)$を発生させるものとします。そしてその力$f(t)$を台車が受け、位置$x(t)$が変わる(動く)というわけですね。
このとき、システム全体のブロック線図は次のように表されます。

プロペラの出力がそのまま台車の入力になっていますね。
いま、プロペラが1次系、台車が2次系であるとすると、このシステム全体は3次系となります(後ほど計算で示します)。
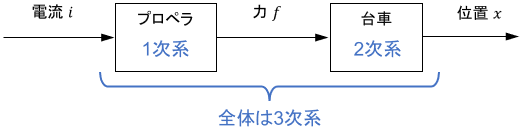
上図のイメージを詳しく説明しましょう。
上記システムの主役は台車ですが、台車のモデル(ブロック)単体では、力$f(t)$が何の制約もなく自由に与えられることを前提としていることになります。(例えば、欲しい力が少しの遅れもなくすぐに与えられるなど)
もちろん現実にはそんなことは不可能です。よって、力を発生させるプロペラの性質を前段に加えることで、$f(t)$の特性(遅れなど)も考慮した「現実的な」モデルが構築されているというわけです。
結果、システム全体が高次系(3次系)になっているとイメージすればOKです。
※1次系・2次系の基本的な性質については、こちらのページをご覧ください
伝達関数の導出
上記システムの伝達関数を実際に計算し、システム全体が高次系となることを数式上でも確認してみましょう。
まず、台車の運動方程式は次式で表されます。
$$m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t)$$
入力は台車に加わる力$f(t)$、出力は台車の位置$x(t)$です。2階の微分方程式なので、台車は2次系ですね。これをラプラス変換して整理すると、台車の伝達関数$G_1(s)$が得られます。
$$X(s) = \ubg{\frac{1}{ms^2 + cs + k}}{G_1(s)}F(s)$$
一方、プロペラの特性は次式で表されるとします。
$$\dot{f}(t) + a f(t)= i(t)$$
入力はプロペラに流される電流$i(t)$、出力は風力$f(t)$です。1階の微分方程式なので、プロペラは1次系ですね。これをラプラス変換して整理すると、プロペラの伝達関数$G_2(s)$が得られます。
$$F(s) = \ubg{\frac{1}{s+a}}{G_2(s)} I(s)$$
これらを結合すると、システム全体、すなわち電流$I(s)$から位置$X(s)$までの伝達関数$G(s)$が得られます。
$$\begin{align}X(s) &= G_1(s) \cdot G_2(s) \cdot I(s)\\\\ &= \frac{1}{ms^2 + cs + k} \cdot \frac{1}{s+a} I(s)\\\\ &= \ubg{\frac{1}{ms^3 + (c+ma)s^2 + (k+ca)s + ka}}{G(s)} I(s)\end{align}$$

確かに、システム全体は3次系となりましたね。2次系と1次系を単純に結合したシステムなので、数式上でも伝達関数をかけ合わせるだけで全体の性質が表現できています。
このように、高次系は伝達関数の基本要素の組み合わせによって得られるシステムだとイメージすればOKです。
高次系の極
次に、このシステムの極を考えてみましょう。
※システムの極については、こちらのページをご覧ください
簡単のため台車$G_1(s)$の極を$p_1,p_2$、プロペラ$G_2(s)$の極を$p_3$とすると、システム全体の伝達関数$G(s)$は次のように変形できます。
$$\begin{align}G(s) &= G_1(s) \cdot G_2(s)\\[5pt] &= \ubg{\frac{\alpha}{(s-p_1)(s-p_2)}}{G_1(s)} \cdot \ubg{\frac{\beta}{s-p_3}}{G_2(s)}\\[5pt]&= \frac{\alpha\beta}{(s-p_1)(s-p_2)(s-p_3)} \end{align}$$
$\alpha,\beta$は、変形の結果出てきたその他の成分をまとめたものです。
ここで注目したいのは、全体システム$G(s)$の極は$p_1,p_2,p_3$となり、$G_1(s),G_2(s)$それぞれの極をそのまま継承するという点です。
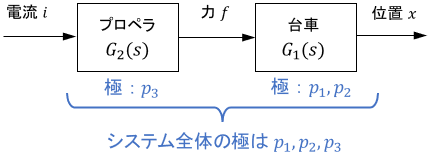
言い換えると、上図のような高次系の極は、それを構成する各要素の極に等しいといえますね。
極はシステムの特性を表すパラメータなので、高次系はそれを構成する各要素の特性(モード)をそのまま継承しているとも解釈できます。
※極$p$によって決定付けられるシステムの特性は「$p$のモード」と呼ばれます。詳細については、こちらのページをご覧ください
複雑な例も本質は同じ!
先ほどの例では、一方のシステムの出力がそのまま他方のシステムの入力となっていました。そのため、個々のシステムの伝達関数を結合するだけでシステム全体の伝達関数を導出できました。
しかしシステムが複雑になると、同じように全体をスッキリとはまとめられなくなります。ただ、このような場合も基本となる考え方は同じですので安心してください。以降、具体例で詳しく説明していきましょう。
伝達関数の導出
先ほどの例にて、プロペラの特性を次式に変更してみます。
$$\dot{f}(t) + a f(t) + \ubg{b\dot{x}(t)}{追加} = i(t)$$
出力$f(t)$が、電流$i(t)$だけでなく台車の速度$\dot{x}(t)$にも依存するようになりました。この場合は方程式が電流$i(t)$・力$f(t)$・位置$x(t)$の3つの変数に基づいているため、先ほどのように入出力関係を単純に表すことができません。
ブロック線図で表すなら、次のようになります。
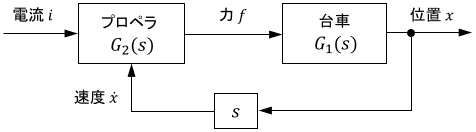
互いの動作が互いに影響を及ぼすので、複雑になっているわけですね。
$$ \left\{ \begin{array}{ll} m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t) &\cdots 台車の方程式\\[3pt] \dot{f}(t) + a f(t) + b\dot{x}(t) = i(t)&\cdots プロペラの方程式 \end{array} \right. $$
これらの式からシステム全体、すなわち電流$I(s)$から位置$X(s)$までの伝達関数$G(s)$を計算してみましょう。先ほどのように伝達関数の単純結合はできませんが、式を連立して$I(s)$と$X(s)$についてまとめるだけでOKです。
まずそれぞれの微分方程式をラプラス変換します。
$$ \left\{ \begin{array}{ll} (ms^2 + cs + k)X(s) = F(s)\\[3pt] (s+a)F(s) + bsX(s) = I(s) \end{array} \right. $$
第1式を第2式に代入して、$F(s)$を消去します。
$$ \Bigl\{ (s+a)(ms^2 + cs + k)+bs \Bigr\}X(s) = I(s) $$
$X(s)$についてまとめると、伝達関数$G(s)$が求まります。
$$\begin{align}X(s) &= \frac{1}{(s+a)(ms^2 + cs + k)+bs} I(s)\\\\ &= \ubg{\frac{1}{ms^3 + (c+ma)s^2 + (k+ca+b)s + ka}}{G(s)} I(s)\end{align}$$
先ほどと同じく、全体は3次系となりましたね。少し複雑になりましたが、本質的には1次系と2次系の組み合わせなので、イメージも先ほどの例と同じです。
システムの極
では、このシステムの極はどのようになるでしょうか?
今回の例は、全体の伝達関数$G(s)$を下位のシステムの伝達関数$G_1(s),G_2(s)$の単純結合で表現できませんでした。言い換えると、全体のシステム$G(s)$は下位のシステム$G_1(s),G_2(s)$の極をそのまま持ちません。
今、全体が3次系であることは分かっているため、全体システムの極が3つであることは確実です。少し逆説的ですが、それらの極を$p_1,p_2,p_3$とすると、全体の伝達関数$G(s)$は次のように変形できます。
$$\begin{align}G(s) &= \frac{1}{ms^3 + (c+ma)s^2 + (k+ca+b)s + ka}\\\\&= \frac{\alpha}{(s-p_1)(s-p_2)(s-p_3)}\end{align}$$
つまり、全体の伝達関数$G(s)$は次のどちらかの組み合わせで表現できると言えますね。
組み合わせ1
- 極$p_1$を持つ1次遅れ要素$\frac{1}{s-p_1}$
- 極$p_2$を持つ1次遅れ要素$\frac{1}{s-p_2}$
- 極$p_3$を持つ1次遅れ要素$\frac{1}{s-p_3}$
組み合わせ2
- 極$p_1$を持つ1次遅れ要素$\frac{1}{s-p_1}$
- 極$p_2,p_3$を持つ2次遅れ要素$\frac{1}{(s-p_2)(s-p_3)}$
※実際、どちらの組み合わせもありえます。それぞれの違いはすぐ後で説明します
言い換えると、複雑なシステムでも結局は伝達関数の基本要素の組み合わせで表現できるわけですね。
今回の場合、それぞれの要素は物理的なシステム構成と1対1で対応しているわけではありませんでしたので、「基本となる動特性(モード)が伝達関数の基本要素として現れ、全体がその結合で表されている」というイメージを持てばOKです。
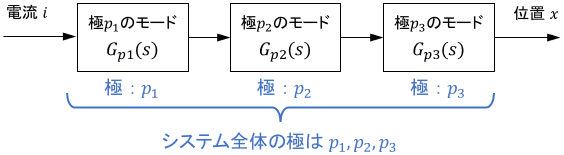
同様の考え方を適用することで、さらに高次のシステムでも基本要素の組み合わせで表現可能です。
2次遅れ要素は、1次遅れ要素2つで表せないときもある

2次遅れ要素は1次遅れ要素2つで表現できるんじゃないの?
だから結局3次系は1次遅れ要素3つの組み合わせになるんじゃないの?
と思うかもしれません。結論から言うと、2次遅れ要素の取り扱い方は次の通りとなります。
- 実極しか持たない2次遅れ要素は、1次遅れ要素2つに分解できる
- 複素極を持つ2次遅れ要素は分解できず、それが基本要素となる
詳しく説明していきましょう。まず、システムが振動的な挙動をする場合、そのシステムは複素極を持ちます。このとき、複素極は$p_1=a+bj$、$p_2=a-bj$と共役なものが必ずセットで現れるのでした($j$は虚数単位、$a,b$は実数)。
※複素極とシステムの挙動に関する詳細は、こちらのページをご覧ください。
このとき、例えば1次遅れ要素$G_{1次}(s)$が複素極$p_1=a+bj$を持とうとすると、
$$G_{1次}(s)=\frac{1}{s-p_1}=\frac{1}{s-\ubg{(a+bj)}{複素数が残る}}$$
となり、伝達関数が複素数を持たなくてはならなくなります。もちろん複素数は仮想的な概念なので、現実にはそのような伝達関数を持つシステムは存在しません。
一方で2次遅れ要素$G_{2次}(s)$が共役な複素極$p_1=a+bj$、$p_2=a-bj$を持とうとすると、
$$\begin{align}G_{2次}(s)&=\frac{1}{(s-p_1)(s-p_2)}\\\\&=\frac{1}{\bigl\{s-(a+bj)\bigr\}\bigl\{s-(a-bj)\bigr\}}\\\\&=\ubg{\frac{1}{s^2-2as+(a^2+b^2)}}{複素数が残らない!}\end{align}$$
となり、伝達関数を実数だけで表現できます。つまり、現実にそのようなシステムが存在可能となります。
以上から、複素極を持つシステムを表せる最小単位は2次遅れ要素であると言えます。伝達関数の基本要素に2次遅れ要素が含まれるのは、このような理由だったわけですね。
もちろん極が実極のみである場合はこのような問題は起こらないので、2次遅れ要素は1次遅れ要素2つに分解できます。高次系を基本要素に分解する場合は、その極に応じて1次遅れ要素・2次遅れ要素を使い分けてくださいね。
以上、高次系の伝達関数と直感的イメージでした。下記ページでは、実用場面でよくでてくる高次系の具体例を紹介していますので、合わせてご覧ください。
- 高次系のほとんどは、伝達関数の基本要素の組み合わせで表現できる
- ある要素の出力が他の要素の入力になっている場合は、それぞれの要素をつなぐだけで全体の(高次の)伝達関数が作れる
- そうでない場合は、微分方程式を整理して伝達関数を導く
- 高次系の極は、それを構成する各基本要素の極に等しい









コメント