このページでは、2次系(2次遅れ系・2次システム)のインパルス応答・ステップ応答の詳細と、よくある使い方を解説します。
※インパルス応答・ステップ応答の詳細については、こちらの記事をご覧ください。
- 2次系の伝達関数は、$G(s)=\frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$で表される。
- $K$はゲインと呼ばれる、出力の大きさを決めるパラメータ
- $\zeta$は減衰係数と呼ばれる、振動の有無と収束速度を決めるパラメータ
- $\omega _n$は固有角周波数と呼ばれる、動作の速度(振動周波数と収束速度)を決めるパラメータ
- 2次系は、振動的な挙動をお手軽に表現するのに便利
2次系の数式モデル
入力$u(t)$と出力$y(t)$の関係が次のような2階の線形微分方程式で表現されるシステムを、2次系(2次遅れ系・2次システム)と呼びます。
$$a_2 \ddot{y}(t) + a_1 \dot{y}(t) + a_0 y(t) = b_0 u(t)$$
ラプラス変換すると、次のようになりますね。
$$ Y(s) = \ubg{\frac{b_0}{a_2 s^2 + a_1 s + a_0}}{伝達関数G(s)} U(s)$$
微分が2回なので、伝達関数の分母の$s$の次数が2になっているのがポイントです。
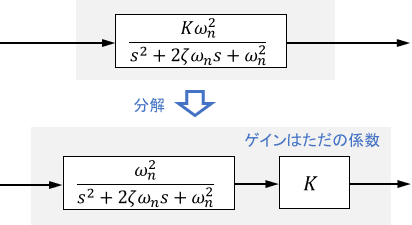
安定な2次系に対しては、各係数の意味を分かりやすくするために、伝達関数$G(s)$を次の形式で表記することがほとんどです。
$$ \begin{gather}G(s) = \frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2} \\\\ ただし、K = \frac{b_0}{a_0}, \quad \zeta = \frac{a_1}{2\sqrt{a_0 a_2}}\geq 0, \quad \omega _n = \sqrt{\frac{a_0}{a_2}} > 0\end{gather}$$
$K$はゲイン、$\zeta$は減衰係数、$\omega _n$は固有角周波数と呼ばれる定数です。2次系の特性は、この3つの定数によって決定づけられます。
ゲイン$K$はただの係数なので、2次系の本質部分は$\frac{ \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$で、その出力の大きさを$K$が決定しているとも解釈できます。

※2次系の具体例については、こちらの記事をご覧ください。
2次系の極
システムの特性を表す重要なパラメータである、極を導出してみましょう。「伝達関数の分母=0」を$s$について解くと、極が得られます。2次方程式の解の公式を使いましょう。
$$\begin{gather}s^2 + 2 \zeta \omega _n s + \omega _n ^2 = 0 \quad を解くと\\[7pt]極: – \omega _n \zeta \pm \omega _n \sqrt{\zeta ^2 – 1} \end{gather}$$
システムの挙動は、システムが実極を持つか複素極を持つか(極が実数であるか複素数であるか)によって大きく変わるのでした。ルートの中身に注目すると、2次系の極は減衰係数$\zeta$の値によって次のように変化することが分かります。
- $0 \leq \zeta < 1$のとき、システムは複素極を持つ(応答が振動する)
- $\zeta = 1$のとき、システムは単一の実極を持つ(応答がギリギリ振動しない)
- $1 < \zeta$のとき、システムは2つの実極を持つ(応答が振動しない)
※実極・複素極とシステムの応答の関係については、こちらのページをご覧ください。
以上を念頭に置きながら、ゲイン$K$・減衰係数$\zeta$・固有角周波数$\omega _n$が、システムのインパルス応答・ステップ応答に及ぼす影響を具体的に見ていきましょう。
インパルス応答・ステップ応答の概要
インパルス応答の波形と傾向
細かい理屈は後にして、まずはインパルス応答の波形を見てみましょう。ゲイン$K$は出力の大きさを決めるパラメータでしたので、減衰係数$\zeta$・固有角周波数$\omega _n$を様々に変えた際のインパルス応答をプロットしてみます。(信号の大きさが同じになるようにゲイン$K$を調整しています)
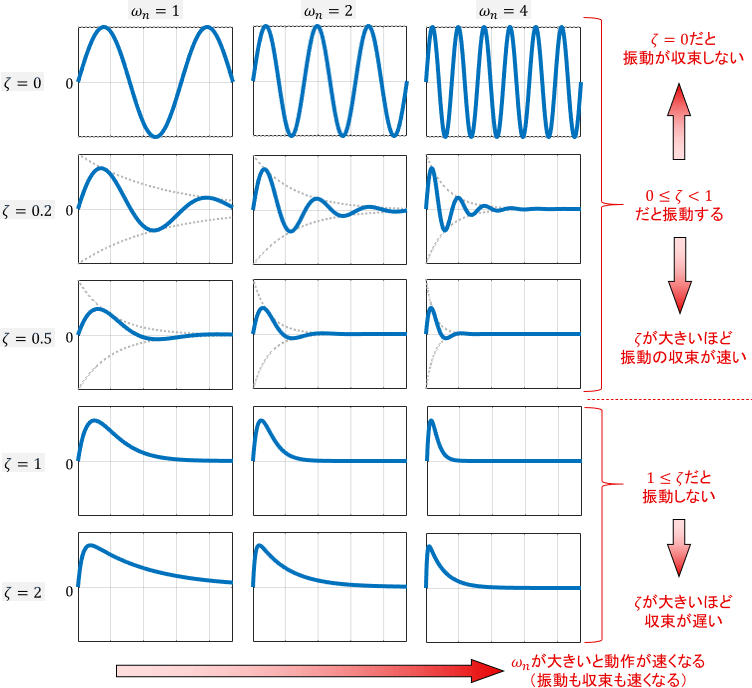

全て0から始まり、それが振動したりしなかったりしながら再び0に収束していますね(一番上を除いて)。
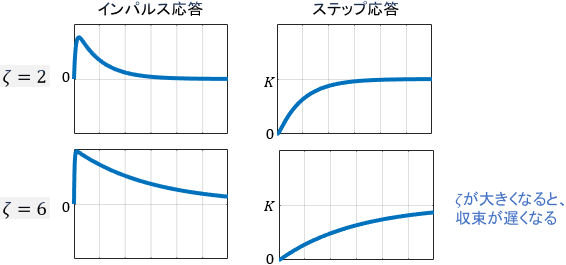
まず、減衰係数$\zeta$の変化に注目しましょう。先ほどの説明の通り、確かに$0 \leq \zeta < 1$のときは応答が振動し、$1 \leq \zeta$のときは振動していませんね。また、応答が振動する$0 \leq \zeta < 1$の範囲では、$\zeta$の値が大きいほど収束が速くなっています。逆に、$\zeta=0$では振動が収束していないことが見て取れます。以上から、減衰係数$\zeta$は振動の有無と収束速度を決めるパラメータであると言えます。
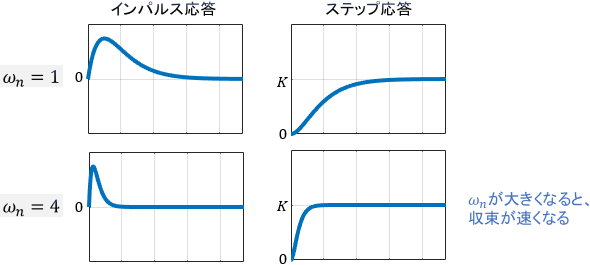
次に、固有角周波数$\omega _n$の変化に注目すると、$\omega _n$が大きくなるほど動作が速くなっていることが見て取れます。振動が速くなっているのはもちろん、それに伴って収束も早くなっていますね。以上から、固有角周波数$\omega _n$は動作の速度(振動周波数と収束速度)を決めるパラメータであると言えます。
ステップ応答の波形と傾向
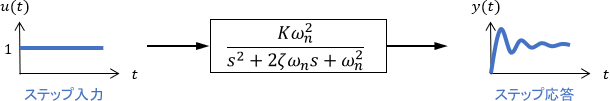
続いて、ステップ応答の波形も確認しましょう。先ほどと同じく、減衰係数$\zeta$・固有角周波数$\omega _n$を様々に変えた際のステップ応答をプロットしてみます。(信号の大きさが同じになるようにゲイン$K$を調整しています)
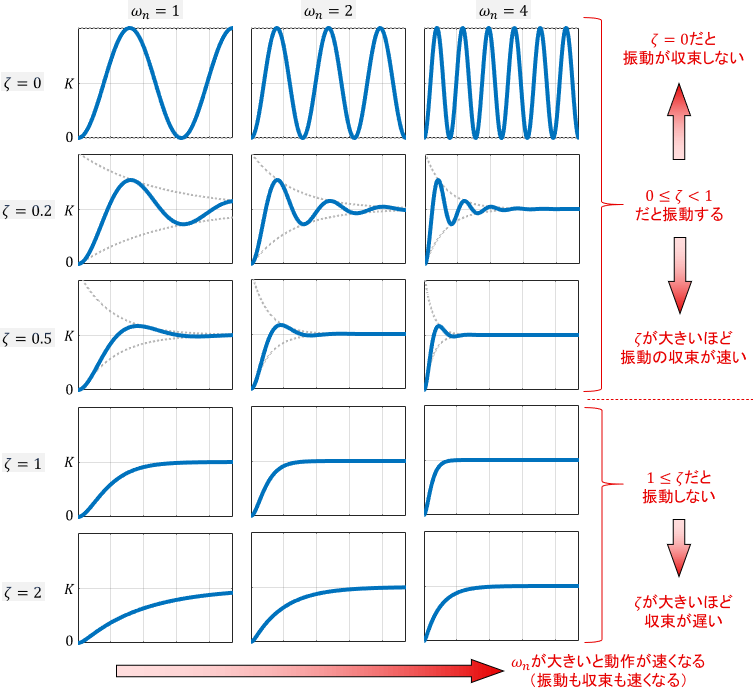

全て0から始まり、それが振動したりしなかったりしながら$K$に収束していますね(一番上を除いて)。
各パラメータの作用は先ほどと同じです。すなわち、減衰係数$\zeta$は振動の有無と収束速度を決め、固有角周波数$\omega _n$は動作の速度(振動周波数と収束速度)を決めるパラメータであることが読み取れます。
インパルス応答・ステップ応答の計算と分析
それでは、各パラメータが上記の作用を持つ理由を、数式から読み解いてみましょう。先ほどの説明の通り、システムの挙動(数式)は$\zeta$の値によって変わるため、それぞれの場合に分けて説明していきます。
※数式が複雑になってきますが、式変形は読み飛ばしても大丈夫です。特に初見の場合は、真面目に式を追ったら途中で読む気がなくなると思うので、計算結果だけ見ればOKです。
システムが複素極を持つ場合の応答
まずはシステムが複素極を持つ場合、すなわち$0 \leq \zeta < 1$の場合を考えます。一言で言うと、システムが振動する場合ですね。
2次系の最大の特徴は振動的な応答であるため、実用上はこの場合が最も重要です。わざわざ伝達関数をゲイン$K$・減衰係数$\zeta$・固有角周波数$\omega _n$で表しているのは、これらで振動の性質をスッキリ表現できるためです。
インパルス応答
システムにインパルス入力$U(s)=1$を与え、インパルス応答$Y(s)$を求めましょう。
$$Y(s)=G(s)U(s)= \frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$$
当然、伝達関数そのものが出てきますね。これを逆ラプラス変換して、$t$領域での挙動を調べます。求め方は色々ありますが、ここでは次の逆ラプラス変換の公式を用います。
$$ \frac{\omega}{(s+a)^2 + \omega ^2} \quad \xrightarrow{\large 逆ラプラス変換}\quad e^{-at}\sin \omega t$$
※ラプラス変換の基礎と各種公式については、こちらのページをご覧ください
インパルス応答$Y(s)$を変形してこの公式に当てはめると、次式が得られます。
$$Y(s) = \frac{K \omega _n}{\sqrt{1-\zeta ^2}}\cdot \frac{\sqrt{1-\zeta ^2}\omega _n}{(s + \zeta \omega _n)^2 + (1-\zeta ^2) \omega _n ^2} \ \xrightarrow{\large 逆ラプラス変換} \ y(t)=\frac{K \omega _n}{\sqrt{1-\zeta ^2}} e^{-\zeta \omega _n t} \sin (\omega _n \sqrt{1-\zeta ^2}t)$$
このインパルス応答をプロットすると、次のようになります。
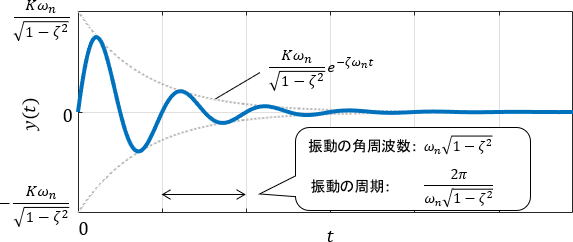

インパルス応答の式とグラフを見比べながら、式の意味を順に解釈していきましょう。
まず、振動的な挙動はsin関数によって生じていることが分かりますね。そして、それにかかる指数関数$e^{-t}$が振動を収束させており、頭についている係数が振動の大きさ(振幅)を決めていると解釈できます。
$$y(t)=\ubg{\frac{K \omega _n}{\sqrt{1-\zeta ^2}}}{大きさ} \cdot \ubg{\vphantom{\frac{K \omega _n}{\sqrt{1-\zeta ^2}}}e^{-\zeta \omega _n t} }{収束} \cdot \ubg{\vphantom{\frac{K \omega _n}{\sqrt{1-\zeta ^2}}}\sin (\omega _n \sqrt{1-\zeta ^2}t)}{振動}$$
まずは、大きさを決める部分$\frac{K \omega _n}{\sqrt{1-\zeta ^2}}$に注目しましょう。形はゴチャゴチャしていますが、結局はただの係数です。ゲイン$K$はここにだけ作用しているので、$\zeta,\omega _n$が何であろうと、$K$を調整することで出力の大きさを自由に決められることが分かります。
次に、収束性を決める部分$e^{-\zeta \omega _n t}$に注目します。指数関数なので、係数の$\zeta \omega _n$が大きいほど収束が速くなります。よって、$\zeta , \omega _n$それぞれが大きければ大きいほど収束が速くなるわけですね。また$\zeta = 0$のときはこの部分が1となるため、振動が収束しなくなることも分かります。
最後に、振動を作り出す部分$\sin (\omega _n \sqrt{1-\zeta ^2}t)$に注目しましょう。この振動の角周波数は$\omega _n \sqrt{1-\zeta ^2}$ですね。よって$\omega _n$が大きいほど、また$\zeta$が小さいほど振動は速くなることが分かります。$\zeta$に注目すると、$\zeta = 0$ のとき(つまり振動が収束しないとき)に振動は最も速くなり、その時の角周波数は$\omega _n$となります。このことから、固有角周波数$\omega _n$は動作速度(振動周波数)の1つの指標となっていることが分かります。
※角周波数の意味とイメージについては、こちらのページをご覧ください。
ステップ応答
システムにステップ入力$U(s)=\frac{1}{s}$を与え、ステップ応答$Y(s)$を求めます。
$$Y(s)=G(s)U(s)=\frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}\cdot \frac{1}{s}$$
逆ラプラス変換するために、(気合で)式を部分分数分解していきます。
$$\begin{align}Y(s)&=K \left( \frac{1}{s} – \frac{s+2\zeta \omega _n}{s^2 + 2\zeta \omega _n s + \omega _n ^2}\right) \\\\&= K \left\{ \frac{1}{s} – \frac{s+\zeta \omega _n}{(s+\zeta \omega _n)^2 + (\omega _n \sqrt{1-\zeta ^2})^2} – \frac{\zeta}{\sqrt{1-\zeta^2}}\cdot \frac{\omega _n \sqrt{1-\zeta^2}}{(s+\zeta \omega _n)^2 + (\omega _n \sqrt{1-\zeta ^2})^2 }\right\}\end{align}$$
これを逆ラプラス変換して、$t$領域での挙動を調べます。次のラプラス変換の公式を当てはめます。
$$ \frac{s+a}{(s+a)^2 + \omega ^2} \quad \xrightarrow{\large 逆ラプラス変換}\quad e^{-at}\cos \omega t$$
$$ \frac{\omega}{(s+a)^2 + \omega ^2} \quad \xrightarrow{\large 逆ラプラス変換}\quad e^{-at}\sin \omega t$$
$$\begin{align} y(t) &= K \left\{ 1 – e^{-\zeta \omega _n t}\cos(\omega _n \sqrt{1-\zeta ^2} t) – \frac{\zeta}{\sqrt{1-\zeta ^2} }\ e^{-\zeta \omega _n t}\ \sin (\omega _n \sqrt{1-\zeta ^2} t) \right\} \\\\ &= K \Bigg\{ 1 – \frac{1}{\sqrt{1-\zeta ^2}}\ e^{-\zeta \omega _n t}\ \sin (\omega _n \sqrt{1-\zeta^2}t + \phi)\Biggr\}\end{align}$$
ただし、$\phi=\tan ^{-1}\Bigl( \frac{\sqrt{1-\zeta^2}}{\zeta}\Bigr)$です。このステップ応答をプロットすると、次のようになります。
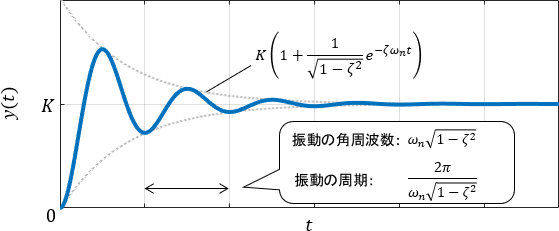

式に注目すると、先ほどと同様に、大きさを決める部分・収束性を決める部分・振動を作り出す部分で構成されていますね。
$$ y(t) = \ubg{\vphantom{\frac{1}{\sqrt{1}}}K}{大きさ} \Bigg\{ 1 – \frac{1}{\sqrt{1-\zeta ^2}}\ \ubg{\vphantom{\frac{1}{\sqrt{1}}}e^{-\zeta \omega _n t}}{収束}\ \ubg{\vphantom{\frac{1}{\sqrt{1}}}\sin (\omega _n \sqrt{1-\zeta^2}t + \phi)}{振動}\Biggr\}$$
式の形は違えど、各部に作用する係数の形は同じであるため、各パラメータと振動特性の関係はインパルス応答の場合と全く同じであることが分かります。
以上、システムが複素極を持つ場合でした。最初に述べた通り実用上はこの場合が最も重要です。以降、システムが実極を持つ場合について解説していきますが、各パラメータの役割は基本的に同じなので、読み飛ばしても構いません。
システムが単一の実極を持つ場合
システムが単一の実極を持つ場合、すなわち$\zeta = 1$の場合を考えます。一言でいうと、システムがギリギリ振動しない場合です。伝達関数に$\zeta = 1$を代入すると、次式が得られます。
$$G(s) = \frac{K\omega _n ^2}{(s+\omega _n)^2}$$
インパルス応答
システムにインパルス入力$U(s)=1$を与え、インパルス応答を求めましょう。逆ラプラス変換の公式一発です。
$$Y(s)=G(s)U(s)=\frac{K\omega _n ^2}{(s+\omega _n)^2}\ \xrightarrow{\large 逆ラプラス変換} \ y(t)=\ubg{K\omega _n ^2}{大きさ}\ t\ \ubg{\vphantom{K\omega _n ^2}e^{-\omega _n t}}{収束}$$
ステップ応答
システムにステップ入力$U(s)=\frac{1}{s}$を与え、部分分数分解します。
$$Y(s)=G(s)U(s)=\frac{K\omega _n ^2}{(s+\omega _n)^2}\cdot \frac{1}{s} = K \left\{ \frac{1}{s} – \frac{1}{s+\omega _n}- \frac{\omega _n}{(s+\omega _n)^2} \right\}$$
後は各項を逆ラプラス変換することで、$t$領域でのステップ応答$y(t)$が得られます。
$$y(t) = K \left( 1 – e^{-\omega _n t} – \omega _n te^{-\omega _n t} \right) = \ubg{K}{大きさ} \bigl\{ 1 – ( 1+ \omega _n t) \ubg{e^{-\omega _n t}}{収束}\bigr\} $$
上式より、インパルス応答・ステップ応答ともに、各パラメータの作用はこれまでと同じであることが分かります。すなわち、ゲイン$K$で出力の大きさが変わり、$e$の右肩にある固有角周波数$\omega _n$が大きいほど収束が速くなるわけですね。

システムが2つの実極を持つ場合
システムが2つの実極を持つ場合、すなわち$1<\zeta$の場合を考えます。一言でいうと、システムが振動しない場合です。
インパルス応答
極$p_1,p_2$を持つシステム$\hat{G}(s)=\frac{1}{(s-p_1)(s-p_2)}$のインパルス応答$\hat{y}(s)$は、次式で得られます。
$$\hat{y}(t) = \frac{1}{p_1-p_2} (e^{p_1 t} – e^{p_2 t})$$
この結果に今考えているシステムの極$p_1 = -\omega _n ( \zeta – \sqrt{\zeta ^2 – 1}), p_2 = -\omega _n ( \zeta + \sqrt{\zeta ^2 – 1})$を代入し、分子の係数$K\omega _n ^2$をかけると、システムのインパルス応答$y(t)$が求まります。
$$y(t) = \ubg{\frac{K \omega _n}{2 \sqrt{\zeta^2 -1}}}{大きさ} \biggl\{ \ubgd{\vphantom{\frac{K \omega _n}{2 \sqrt{\zeta^2 -1}}}e^{-\omega _n ( \zeta – \sqrt{\zeta ^2 – 1})t}}{極p_1のモード}{(の収束)} \ \ubgd{\vphantom{\frac{K \omega _n}{2 \sqrt{\zeta^2 -1}}}-e^{-\omega _n ( \zeta + \sqrt{\zeta ^2 – 1})t}}{極p_2のモード}{(の収束)}\biggr\}$$
ステップ応答
極$p_1,p_2$を持つシステム$\hat{G}(s)=\frac{1}{(s-p_1)(s-p_2)}$のステップ応答$\hat{y}(s)$は、次式で得られます。
$$\hat{y}(t) = \frac{1}{p_1(p_1-p_2)} e^{p_1 t} – \frac{1}{p_2(p_1-p_2)} e^{p_2 t} + \frac{1}{p_1 p_2}$$
この結果に今考えているシステムの極$p_1 = -\omega _n ( \zeta – \sqrt{\zeta ^2 – 1}), p_2 = -\omega _n ( \zeta + \sqrt{\zeta ^2 – 1})$を代入し、分子の係数$K\omega _n ^2$をかけると、システムのステップ応答$y(t)$が求まります。
$$y(t) = \ubg{\vphantom{\frac{\zeta + \sqrt{\zeta^2 – 1}}{2\sqrt{\zeta^2 -1}}}K}{大きさ} \Biggl\{ 1\ \ubg{- \frac{\zeta + \sqrt{\zeta^2 – 1}}{2\sqrt{\zeta^2 -1}}e^{-\omega _n ( \zeta – \sqrt{\zeta ^2 – 1})t}}{極p_1のモード(の収束)} + \ubg{\frac{\zeta – \sqrt{\zeta^2 – 1}}{2\sqrt{\zeta^2 -1}}e^{-\omega _n ( \zeta + \sqrt{\zeta ^2 – 1})t}}{極p_2のモード(の収束)} \Biggr\}$$
※式の詳しい導出と、モードの詳細については、こちらのページをご覧ください。
実極が2つあるので、インパルス応答もステップ応答も2つの動作モードを持ちますが、各パラメータの作用はこれまでと同じです。すなわち、ゲイン$K$で出力の大きさが変わり、$e$の右肩にある固有角周波数$\omega _n$が大きいほど収束が速くなります。
残りの減衰係数$\zeta$も、$e$の右肩で各モードの収束速度を決めています。詳細は省きますが、下図のように$\zeta$が大きいほど収束は遅くなります。(インパルス応答のピークは速くなります)

2次系の使い方
ここからは、2次系のよくある使い方について解説していきます。
当然ですが、対象が本質的に2次系である場合は、それを$G(s)=\frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$とモデリングし、分析・制御すればOKです。
ただ、2次系はシンプルで扱いやすいため、これ以外にも様々な場面で利用されます。代表的な例は、振動的な挙動をお手軽に表現したい場面です。これについて、詳しく説明していきます。
例えば今、ロボットアームをモーターで動かしたいとしましょう。実際に動かしてみたところ、動作がガタガタと振動してしまったとします。
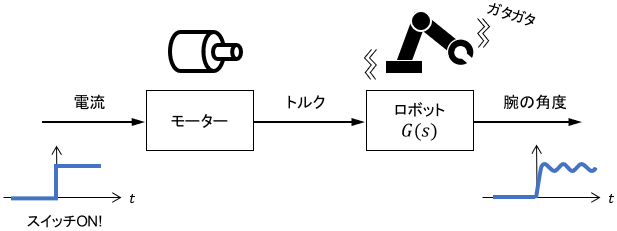

どうもモーターの性能が悪く、ロボットアームに加えられるトルクが振動していることが原因のようです。こんなときはモーターの特性を伝達関数で表し、それに基づいて入力電流を制御できればよいのですが、モーターの特性がよく分かっていないとします。
このような場合は、下図のようにモーターを2次系で近似的にモデル化することで、とりあえず振動的な挙動を表現できます。


パラメータ設定も簡単で、ゲイン$K$で信号の大きさを、減衰係数$\zeta$と固有角周波数$\omega _n$で振動の周波数と収束速度を調整するだけです。
当然、厳密にモーターの特性を数式化したほうがモデルの精度は高くなりますが、精度よりも式の単純性が求められる場合や、とりあえずお手軽に実装してざっくりと効果を確認したい場合は、このような近似が非常に有効です。
以上、2次系のインパルス応答・ステップ応答と、使い方の解説でした。
※こちらのページでは、周波数応答の観点から2次系の特性と使い方を解説していますので、合わせて覧ください
- 2次系の伝達関数は、$G(s)=\frac{K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$で表される。
- $K$はゲインと呼ばれる、出力の大きさを決めるパラメータ
- $\zeta$は減衰係数と呼ばれる、振動の有無と収束速度を決めるパラメータ
- $\omega _n$は固有角周波数と呼ばれる、動作の速度(振動周波数と収束速度)を決めるパラメータ
- 2次系は、振動的な挙動をお手軽に表現するのに便利










コメント