このページでは、2次系(2次遅れ系・2次システム)の周波数特性とボード線図について、具体例を交えて詳しく解説します。
また、2次系のよくある使い方についても解説します。
※周波数応答やボード線図の基礎を未学習の方は、まずこちらのページをご覧ください。
- 2次系は「信号の低周波成分はそのまま通し、高周波成分は周波数が高ければ高いほどカットする」という性質を持つ
- また、中間の周波数成分を増幅させることがある(共振)
- 1次系よりも強力に高周波成分をカットするローパスフィルタとして使える。
2次系のボード線図
次の伝達関数で表される、2次系の周波数特性を考えましょう。
$$G(s) = \frac{ \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2} $$
$\zeta$は減衰係数、$\omega_n$は固有角周波数と呼ばれる正の定数です。
特に減衰係数$\zeta$の値によって、2次系の挙動は大きく変化するのでしたね。
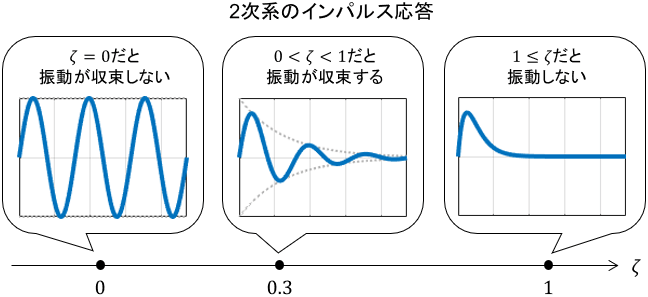

※2次系の数式表現や、基本的な挙動については、こちらのページをご覧ください
当然、周波数特性を表すボード線図も、$\zeta$の値によって変化します。例えば$\omega_n=10$[rad/s]として、$\zeta$を様々に変化させたときのボード線図は、次のようになります。
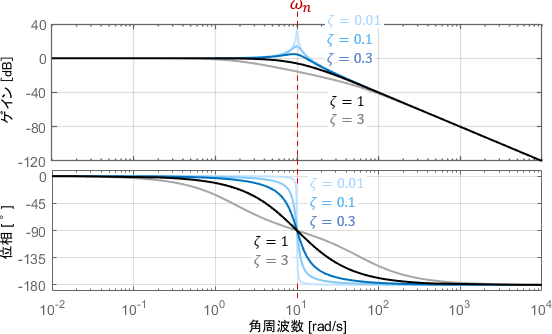

ここからは、上図を例に2次系のボード線図を詳しく読み取っていきましょう。
※ちなみに$\frac{ K \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$のように伝達関数に定数ゲイン$K$がかかる場合は、$K$と$\frac{ \omega _n ^2}{ s^2 + 2 \zeta \omega _n s + \omega _n ^2}$を別々のシステムと見なし、それぞれのボード線図を足し合わせればOKです($K$は定数なので、結局ゲイン線図が$K$倍分上にずれるだけになります)。ボード線図の足し合わせの法則については、こちらのページをご覧ください。
ゲイン線図
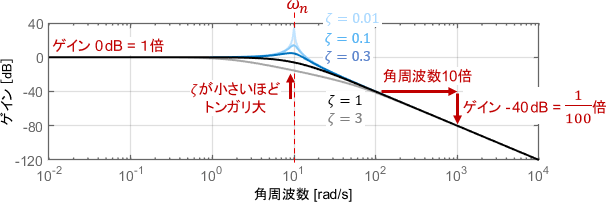

まずゲイン線図に注目すると、$\omega _n$より低い角周波数ではだいたいゲインが0dBとなっています。よって、角周波数が$\omega _n$以下の信号成分はそのままの大きさで出力される(システムをそのまま通過する)ことが分かります。
一方で$\omega _n$よりも高い角周波数では、角周波数が10倍になるごとに(つまり1decadeごとに)ゲインが40dBずつ小さくなっています。よって、角周波数が$\omega _n$以上の信号成分は周波数が高ければ高いほど減衰して出力される(カットされる)ことが分かります。
また、このように「1decadeごとに信号が-40dB分カットされる」という特性は、-40dB/decと表現されたりもします。
最後に角周波数$\omega _n$付近でのゲインに注目すると、$\zeta$が小さいほど大きなトンガリが生じていることが分かります。トンガリ部分のゲインは0dBよりも大きいため、角周波数$\omega _n$付近の信号成分は増幅して出力されるというわけですね。(後ほどの例で、具体的なイメージを説明します)
位相線図
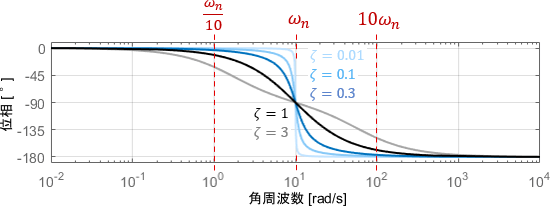

一方の位相線図からは、次の性質が読み取れます。
- $\frac{\omega _n}{10}$以下では位相がだいたい0°(信号が遅れない)
- $\omega _n$では位相が-90°(信号が90°遅れる)
- $10 \omega _n $以上では位相がだいたい-180°(信号が180°遅れる)
減衰係数$\zeta$に対しては、$\zeta$が小さいほど0°から180°への位相の変化が急になっていることが分かりますね。
ボード線図の具体例と直感的イメージ
2次系の例:ばねダンパシステム
ここからは、上で読み取ったボード線図の物理的な意味を考えることで、直感的イメージを深めていきましょう。
例として次の機械システムを考えましょう。入力はブロックに加わる力$f(t)$、出力はブロックの位置$x(t)$です。
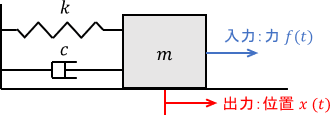

このシステムの伝達関数は、次式で得られます。
$$G(s)=\frac{1}{ms^2 + cs + k}$$
※その他の2次系の例は、こちらの記事をご覧ください。具体的なシステムが何であれ、対象が2次系であれば、その直感的イメージは以下の説明と同じです
今回は、$K=1,\ \omega _n=10,\ \zeta = 0.3$となるように物理定数$m,c,k$を設定することとしましょう。このとき、ボード線図は次のようになります。
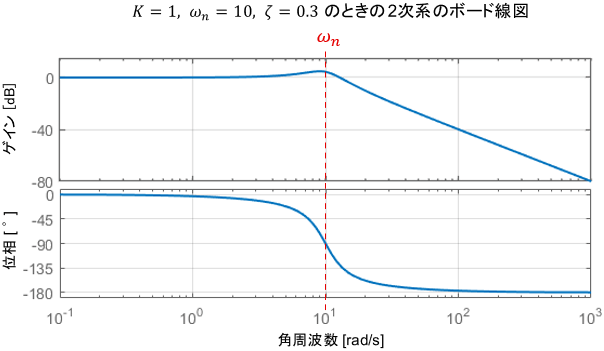

2次系の特徴であるトンガリが現れていますね。
このシステムに様々な周波数の力を入力し、その出力から周波数特性を理解していきましょう。

低周波特性のイメージ
まず、そこそこ遅い入力$f(t)$として、1[rad/s]のsin波を与えてみましょう。この入力信号に対する特性は、ボード線図の1[rad/s]の部分を読み取れば分かります。
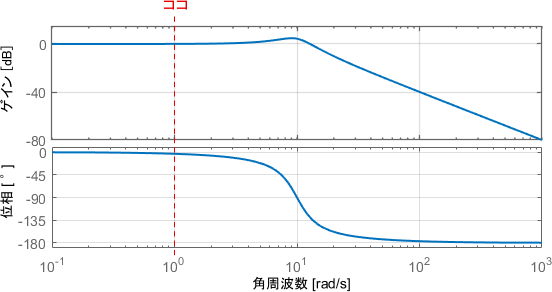

このときのシステムの挙動は、次のようになります。
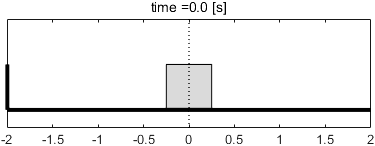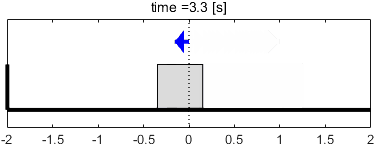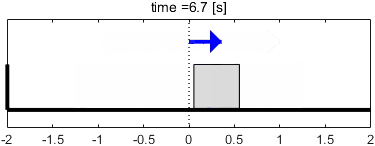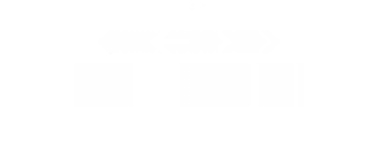

※上の青矢印が、ブロックに加わる入力$f(t)$の向きと大きさを表しています。また、バネとダンパの描画は省略しています(以降も同じです)。
このときの入出力信号の波形も見てみましょう。
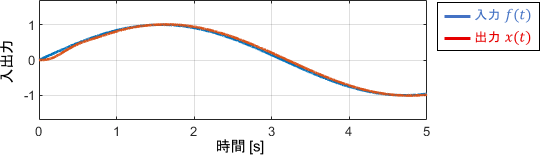

入力と出力がほぼ一致しているような挙動が得られていますね。ボード線図と照らし合わせて、この挙動を読み取ってみましょう。
まずゲイン線図に注目すると、ゲインは0dB(つまり1倍)となっています。出力信号の振幅を見ると、確かに入力信号の振幅と変わっていませんね。
続いて位相線図に注目すると、位相遅れはほぼ0°となっています。信号にほとんど遅れが生じないので、結果的に入力と出力がほぼ一致しているというわけですね。
中周波特性のイメージ
次に、入力$f(t)$として10[rad/s]のsin波を与えてみましょう。この入力信号に対する特性は、ボード線図の10[rad/s]の部分を読み取れば分かります。
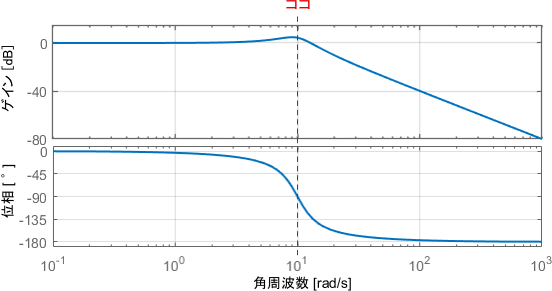

ちょうどトンガリのあたりですね。このときのシステムの挙動と、入出力信号の波形を見てみましょう。
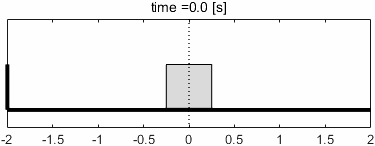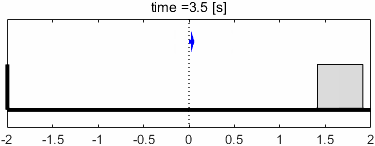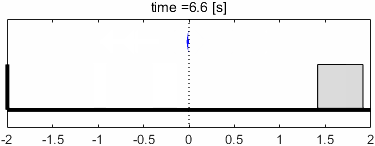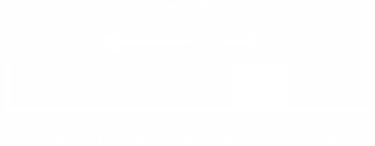

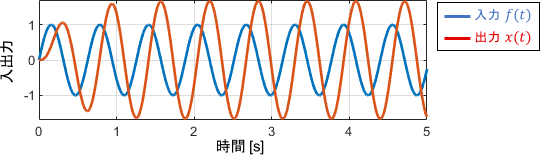

定常状態での入出力の振幅に注目すると、入力よりも出力の振幅が大きくなっていることが分かります。ゲインが正の値(約4.5dB)なので、その分信号が増幅されているわけですね。
これを物理的に解釈すると、この周波数にて共振が生じていることになります。
例えば重りのついたバネや、薄い板などを手に持ってビヨビヨ揺らすことを想像してみてください。このとき、対象に合った特定のリズムで力を加えると、小さな力でも対象を大きくビヨンビヨン揺らせますよね。
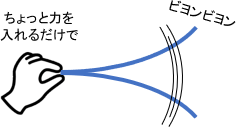

ゲイン線図のトンガリでは、システムのこのような性質が現れていると解釈すればOKです。
一方で入出力の位相(タイミング)に注目すると、出力の挙動が入力に対して少し遅れて(ズレて)いることが分かります。その遅れ量は、位相線図より90°(sin波$\frac{1}{4}$個分)であることが読み取れます。信号波形を見ると、確かにそれだけ遅れていますね。
入力信号が速くなるにつれ、出力がだんだんとついていけなくなっている様子が現れていると解釈すればOKです。
高周波特性のイメージ
最後に、そこそこ速い入力$f(t)$として、100[rad/s]のsin波を与えてみましょう。この入力信号に対する特性は、ボード線図の100[rad/s]の部分を読み取れば分かりますね。
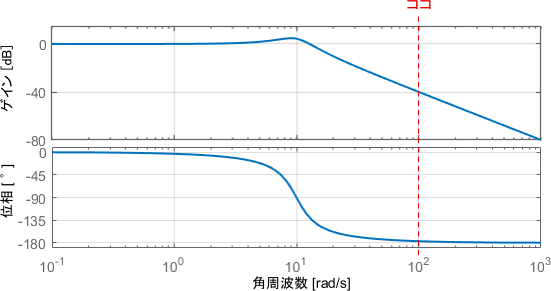

このときのシステムの挙動と、入出力信号の波形を見てみましょう。
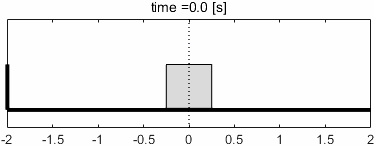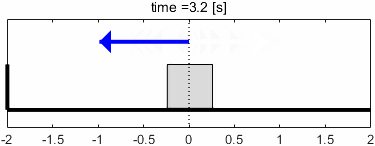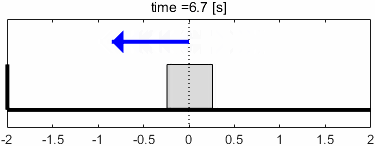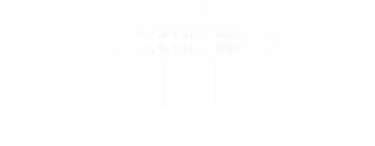

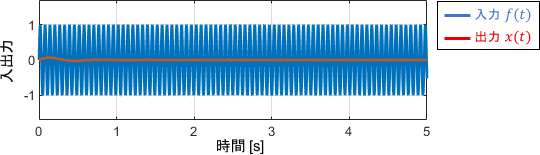

入力が速すぎて、ブロックがほとんど動いていませんね。これをボード線図上で解釈してみましょう。
ゲイン線図に注目すると、ゲインは-40dB(つまり0.01倍)となっています。ブロックの動きがほとんどなくなっていることが、ここに現れていますね。
続いて位相線図に注目すると、位相は180°(sin波半個分)遅れていることが分かります。ただし、そもそも出力がなくなっているような状態なので、位相はほとんど意味をなさなくなっているといえるでしょう。
2次系のボード線図のポイント
「振動する=トンガリがある」ではない!


ほーん。じゃあシステムが振動する$0\leq \zeta<1$のときに共振が起きて、ゲイン線図にトンガリができるんだな。


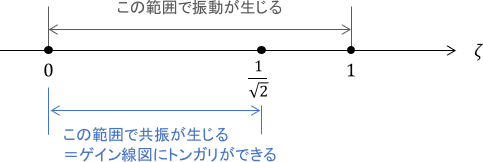
と思うかもしれませんが、「システムが振動する=共振が起きてゲイン線図にトンガリができる」ではないことに注意してください。
実際のところ、共振は$0\leq \zeta<\frac{1}{\sqrt{2}}$のときに生じ、このときにのみゲイン線図はトンガリを持ちます。($\frac{1}{\sqrt{2}}$はだいたい0.7くらいです)

減衰係数$\zeta$を様々に変化させたときの、ゲイン線図のトンガリの様子がこちらです。
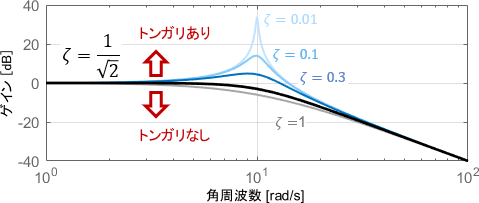

確かに$\zeta=\frac{1}{\sqrt{2}}$のときには、ゲイン線図にトンガリが生じていませんね。このとき、システムは「振動するが共振しない」という状態になっているわけです。
「$\zeta=\frac{1}{\sqrt{2}}$を境界線として、トンガリの有無が変わる」というイメージを持っておきましょう。
「トンガリのピーク=固有角周波数」ではない!


ほーん。じゃあ$0\leq \zeta<\frac{1}{\sqrt{2}}$のときにトンガリができて、その場所は$\omega_n$なんだな。
確かにトンガリの場所は固有角周波数$\omega _n$のあたりで間違いないのですが、そのピークは$\omega _n$から少しズレた所であることも抑えておきましょう。
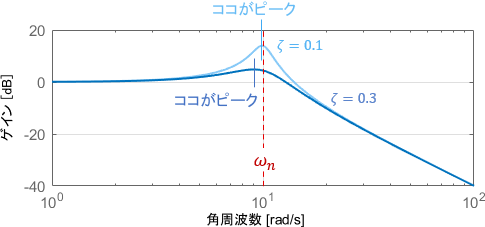

トンガリのピークでは共振が最も大きくなるので、その角周波数には共振角周波数という固有の名前がついています。
この共振角周波数$\omega _p$と固有角周波数$\omega _n$には、次の関係があることが知られています。
$$\omega _p = \omega _n \sqrt{1-2\zeta ^2}$$
トンガリができる$\zeta$の範囲は$0\leq \zeta<\frac{1}{\sqrt{2}}$だったことを考えると、上式は次のように解釈すればよいことになります。
- $\zeta$が小さくなる(ピークが高くなる)ほど、$\omega _p$は$\omega _n$に近くなる
- $\zeta$が$\frac{1}{\sqrt{2}}$に近くなる(ピークが低くなる)ほど、$\omega _p$は$\omega _n$より低い方向に遠ざかる
最初は「$\omega _p$は$\omega _n$からちょっと低い側にズレる」と覚えておけば問題ないでしょう。
2次系の使い方(周波数特性の観点で)
ここからは、周波数特性の観点で見た、2次系の使い方について解説していきましょう。
※こちらのページでは、インパルス応答・ステップ応答の観点から2次系の使い方を解説していますので、合わせて参考にしてください
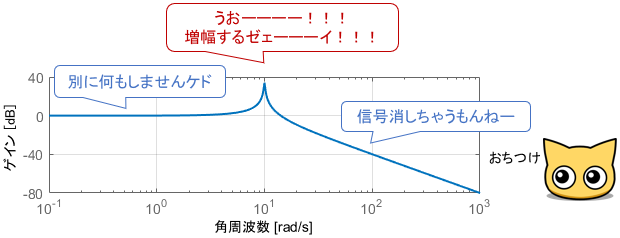
トンガリは基本的に悪いもの
上述の通り、2次系は$0\leq \zeta<\frac{1}{\sqrt{2}}$のときにゲイン線図にトンガリを持ち、$\omega _n$付近の信号成分を増幅させるという他のシステムにはない特徴を持っています。
信号を増幅させると聞くとお得な感じがしますが、実用上はこのような特性は結構危険なものであり、取り扱いに注意が必要です。
極端な例として、トンガリを持つ2次系の出力をそのままフィードバックし、再び入力とすることを考えてみましょう。
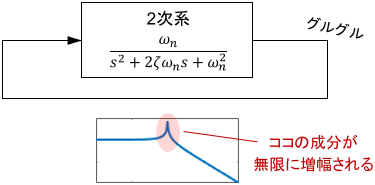

当然、フィードバックループを回るたびに$\omega _n$付近の信号成分が無限に増幅され、最後には発散してしまいますよね。
ここまで極端でなくとも、トンガリは「一部の信号がハリキリすぎて余計なことをする」ような状態であるため、システムに意図しない悪影響を及ぼすことが多いです。
よって基本的には、ゲイン線図にトンガリを持たない2次系のほうが実用上使いやすいと言えるでしょう。増幅したり減衰したりと、信号成分に応じて特性がコロコロ変わるシステムは、そりゃ使いにくいですよね。

ローパスフィルタ
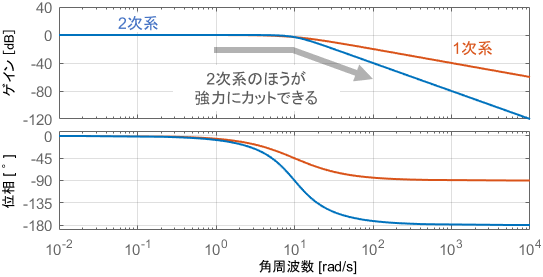
それを踏まえて、2次系の具体的な使い方を見ていきましょう。代表的な使い方としては、1次系と同じくローパスフィルタが挙げられます。
1次系は高周波領域にて-20dB/decずつ信号が減衰するのに対し、2次系は-40dB/decで減衰するため、2次系は1次系よりも強力に高周波成分をカットできると言えます。

※1次系の周波数特性については、こちらのページをご覧ください
ただ、2次系は減衰係数$\zeta$の値によってその性質が変わるのでした。ここからは、ローパスフィルタとして2次系を用いる際の、適切な$\zeta$の値について考えてみましょう。
まず、$\zeta$の値に関わらず、低周波領域ではゲイン0dB・位相0°、高周波領域ではゲイン-40dB/dec・位相-180°となるのが2次系の基本的な周波数特性でしたね。
ローパスフィルタとして使う場合は、これらの特性が、カットの境界となる角周波数$\omega _n$にて瞬時に切り替わることが理想であると言えます。
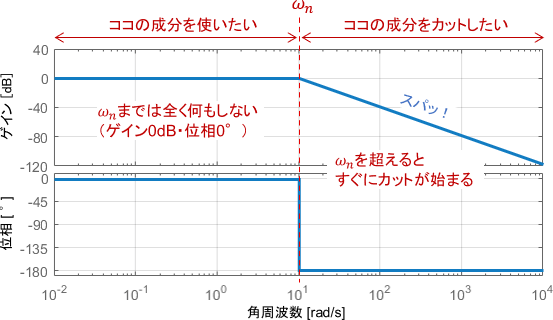

上図のような状態を実現する$\zeta$は残念ながら存在しないのですが、最も近い値としては$\zeta=\frac{1}{\sqrt{2}}$が挙げられます。先ほど出た、ゲイン線図にトンガリがギリギリ現れない値ですね。
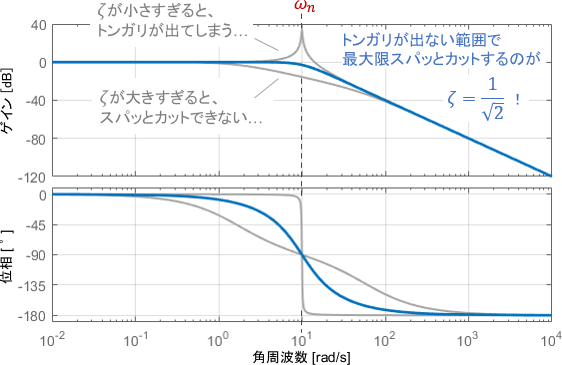

これにより、トンガリが出ない範囲で信号を最大限スパッとカットできることになります。
同じ1次系を2つ重ねただけ(つまり$\zeta=1$のとき)ではこれほどのカット特性は得られないため、これは2次系ならではの特別な強みであると言えるでしょう。
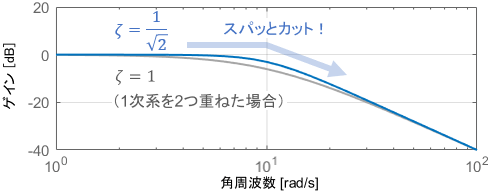

※$1\leq\zeta$のとき、2次系は1次系2つの重ね合わせで表現できます(極が実数となるため)。詳細については、こちらのページの後半をご覧ください
フィルタ設計の分野では、この$\zeta=\frac{1}{\sqrt{2}}$のときの特性を、(2次の)バターワース特性と呼んだりもします。
以上、2次系の周波数特性とボード線図についての解説でした。
- 2次系は「信号の低周波成分はそのまま通し、高周波成分は周波数が高ければ高いほどカットする」という性質を持つ
- また、中間の周波数成分を増幅させることがある(共振)
- 1次系よりも強力に高周波成分をカットするローパスフィルタとして使える。










コメント