このページでは、安定余裕(ゲイン余裕・位相余裕)について、その意味と直感的イメージを解説します。また、ベクトル軌跡やボード線図から安定余裕を読み取る方法についても、詳しく解説します。
- 安定余裕は「フィードバック制御システムが内部安定だとしたときに、それがどれくらい安定であるか」を示す指標
- 安定余裕からは「数式モデルの誤差がどれほどまでなら許容されるか」が分かる
- ゲイン余裕は「ゲイン何倍相当の誤差までなら許容されるか」を表す
- 位相余裕は「位相何度相当の誤差までなら許容されるか」を表す
安定余裕とは
安定余裕とは、「フィードバック制御システムが安定(内部安定)だとしたときに、それがどれくらい安定であるかを示す指標」です。詳しい説明の前に、まずはざっくりとしたイメージについて解説していきましょう。
安定余裕は、フィードバック制御システムの内部安定性を判別する、ナイキストの安定判別法を応用することで得られる概念です。
ナイキストの安定判別法は、次のようなものでしたね。
次のブロック線図で表される、開ループ伝達関数が安定なフィードバック制御システムにおいて、
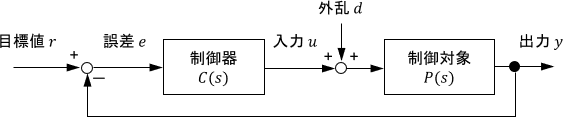

- 開ループ伝達関数のベクトル軌跡$C(j\omega)P(j\omega)$を描き、
- それが点(-1,0)を左に見ながら原点に向かえば、システムは内部安定
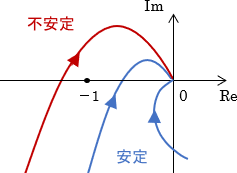

超ざっくり言うと、開ループ伝達関数のベクトル軌跡が点(-1,0)を境に左側にあれば不安定で、右側にあれば安定であるというわけですね。
※上記は簡易版のナイキストの安定判別法です。本ページでは説明をシンプルにするために、簡易版を用いて説明していきます。ナイキストの安定判別法(簡易版・通常版)については、こちらのページをご覧ください。
※以降、表記をシンプルにするために「フィードバック制御システムの開ループ伝達関数のベクトル軌跡」のことを単に「ベクトル軌跡」と記載します。
ただし、実用上は数式モデルに誤差が含まれるため、注意が必要です。当然、誤差があればそれに応じて軌跡もズレてしまいますよね。
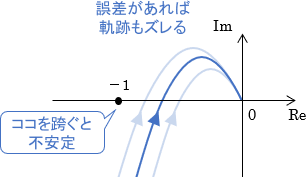

たとえ数式上はシステムが安定であっても、誤差によってベクトル軌跡が点(-1,0)を跨いでしまえば、現実には不安定になってしまいます。
このため、実用上はベクトル軌跡と点(-1,0)の間に、誤差によって多少ズレても問題ないくらいの余裕が必要となります。
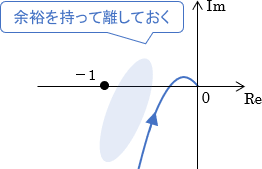

この余裕の大きさを、「ベクトル軌跡と点(-1,0)との近さ」によって表したものが安定余裕です。
ベクトル軌跡上の安定余裕
で、この「ベクトル軌跡と点(-1,0)との近さ」をどう表現するかですが、実用上はゲイン余裕・位相余裕という指標が使われることがほとんどです。
ゲイン余裕・位相余裕は、次のように表されます。
- ゲイン余裕:位相そのままでゲインをあと何倍すると軌跡が点(-1,0)に触れるか
- 位相余裕:ゲインそのままで位相があと何度遅れると軌跡が点(-1,0)に触れるか
これらは、ベクトル軌跡から次のように読み取ることができます。


これらについて、詳しく説明していきましょう。
※ゲイン・位相は、システムの周波数特性を表す指標です。詳細は、こちらのページをご覧ください
ベクトル軌跡上のゲイン余裕
まずはゲイン余裕、つまり「位相そのままでゲインをあと何倍すると軌跡が点(-1,0)に触れるか」について考えます。
もし、システムの位相がそのままでゲインが$K$倍された場合、そのベクトル軌跡は原点を中心に$K$倍拡大(or縮小)されるのでした。
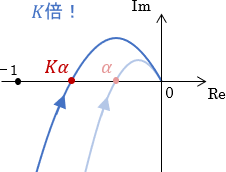

上図の通り、ゲインを$K$倍すると横軸との接点$\alpha$も$K$倍され、$K\alpha$となっていますね。
※ベクトル軌跡とゲイン・位相の関係性については、こちらのページをご覧ください
この点が-1に触れると安定性が崩れるため、ゲイン余裕は次式で計算できることになります。
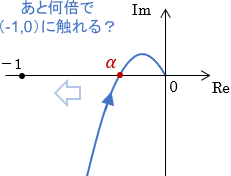

$$ゲイン余裕=\frac{1}{|\alpha|}\ [倍]$$
$\alpha$は負の数なので、点(-1,0)との距離だけを考えるために絶対値が付いています。
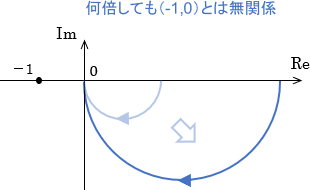
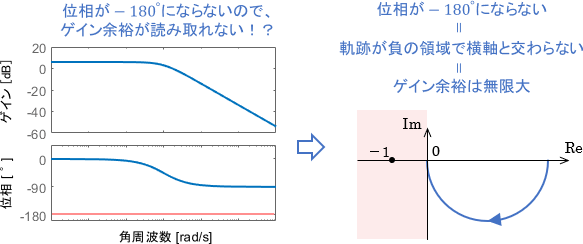
ちなみに、下図のようにベクトル軌跡が負の領域で横軸と交わらない場合は、ゲインを何倍しても点(-1,0)に届くことはないので、ゲイン余裕は無限大ということになります。

ベクトル軌跡上の位相余裕
続いては位相余裕、つまり「ゲインそのままで位相があと何度遅れると軌跡が点(-1,0)に触れるか」について考えましょう。
もし、システムのゲインがそのままでシステム全体の位相が$\theta$[°]遅れた場合、そのベクトル軌跡は原点を中心に$\theta$[°]だけ回転するのでした。
![もしシステム全体の位相がθ[rad]遅れた場合、そのベクトル軌跡は原点を中心にθ[rad]だけ回転する例](https://controlabo.com/wp-content/uploads/2022/05/vector_locus_rotate.png)
![もしシステム全体の位相がθ[rad]遅れた場合、そのベクトル軌跡は原点を中心にθ[rad]だけ回転する例](https://controlabo.com/wp-content/uploads/2022/05/vector_locus_rotate.png)
回転した結果、ベクトル軌跡が点(-1,0)に触れると安定性が崩れるため、位相余裕は下図の$\phi$で求められることになります。
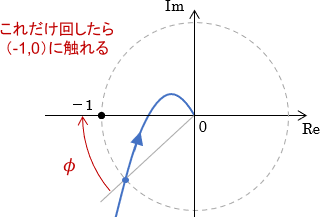

※位相余裕の単位には、[°]の他に[rad]が使われることもあります。どちらも上記$\phi$の角度を表しているだけで、本質的には同じものです。
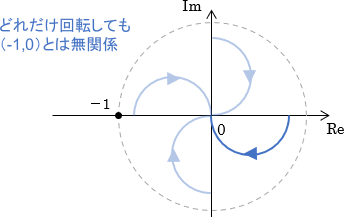
ちなみに下図のように、ベクトル軌跡が「原点からの距離が1の点」を持たない場合は、位相がどれだけ変化しても点(-1,0)に届くことはないので、位相余裕は無限大ということになります。

ボード線図上の安定余裕
上記と同じ考えで、ゲイン余裕・位相余裕をボード線図から読み取ることも可能です。実用上はベクトル軌跡よりもボード線図を用いることのほうが非常に多いため、ボード線図での読み方もしっかり抑えておきましょう。
具体的には、ゲイン余裕・位相余裕は、開ループ伝達関数$C(s)P(s)$のボード線図上で次のように読み取ることが可能です。
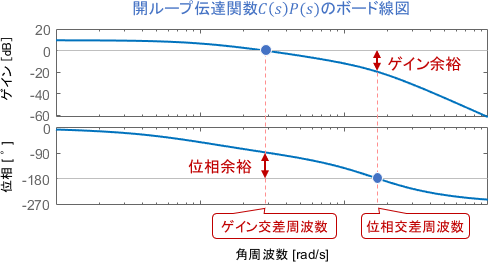

安定余裕(とその元になるナイキストの安定判別法)は、システムの開ループ伝達関数のベクトル軌跡によるものだったので、ボード線図も開ループ伝達関数のものを見ることに注意してください。
ここからは、ゲイン余裕・位相余裕が上記のように読み取れる理由について、解説していきましょう。
※ボード線図とゲイン・位相の関係性については、こちらのページをご覧ください
ボード線図上のゲイン余裕
ゲイン余裕は、ベクトル軌跡上で「位相そのままでゲインをあと何倍すると軌跡が点(-1,0)に触れるか」を読み取ることで分かるのでした。
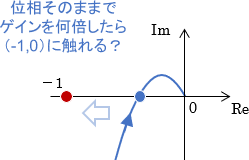

ベクトル軌跡上の点(-1,0)は、ボード線図上で「ゲイン0dB(=1倍)、位相-180°となる点」に相当します。よって「ベクトル軌跡上で点(-1,0)に触れる」ということは、「ボード線図上でゲイン0dB・位相-180°の点に触れる」ということに等しくなります。
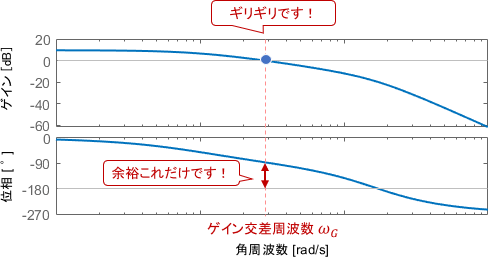
このことから、ボード線図上でのゲイン余裕は、下図のように「位相が-180°となる周波数にて、ゲインをあと何dB上げると線が0dBに触れるか」によって読み取れることになります。


●と●が、ベクトル軌跡とボード線図で同じ点を意味していることを確認してみてください。
ちなみに「位相が-180°となる周波数」は、位相交差周波数とも呼ばれます。
※ボード線図ではゲインの倍率がデシベル値で表されるため、読み取られるゲイン余裕の単位も[dB]となります。デシベル値と倍率の関係性については、先ほど紹介したボード線図のページをご覧ください。
なお、位相交差周波数にてゲインが0dBを通り過ぎてしまっている(上回る)場合、これはベクトル軌跡が点(-1,0)を右にみることに相当しますので、そもそもシステムは不安定であることになります。


●と●の位置関係が、さっきの図とちょうど反対になっているのがポイントです。
また、ボード線図上で位相が-180°となる点がない(=位相交差周波数がない)場合、これはベクトル軌跡が負の領域で横軸と交わらないことに相当しますので、ゲイン余裕は無限大ということになります。

ボード線図上の位相余裕
位相余裕は、ベクトル軌跡上で「ゲインそのままで位相があと何度遅れると軌跡が点(-1,0)に触れるか」を読み取ることで分かるのでした。
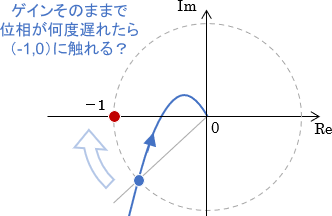

また、「ベクトル軌跡上の点(-1,0)」は「ボード線図上でゲイン0dB・位相-180°の点」に対応するのでしたね。
これらを踏まえると、ボード線図上での位相余裕は、「ゲイン0dBとなる周波数にて、位相があと何度遅れると線が-180°に触れるか」によって読み取れることになります。
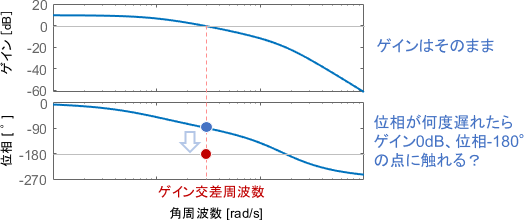

こちらも、●と●がベクトル軌跡とボード線図で同じ点を意味しているので、比べてみてください。
ちなみに「ゲインが0dBになる周波数」は、ゲイン交差周波数とも呼ばれます。
なお、ゲイン交差周波数にて位相が-180°を通り過ぎてしまっている(下回る)場合、これはベクトル軌跡が点(-1,0)を右に見ることに相当しますので、そもそもシステムは不安定であることになります。
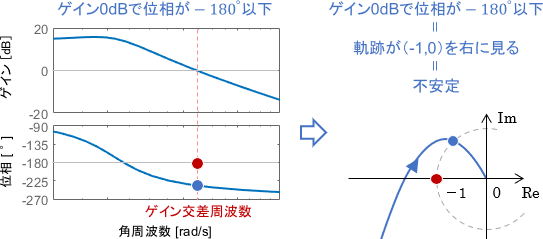

また、ボード線図上でゲインが0dBになる点がない(=ゲイン交差周波数がない)場合、これはベクトル軌跡が「原点からの距離が1の点」を持たないことに相当しますので、位相余裕は無限大ということになります。


※ちなみにこちらのサイトでは、入力した伝達関数に対し、安定余裕を含め様々な性質を自動で計算してくれます。
安定余裕のイメージ


ほーん。とりあえず安定余裕を読み取れるようにはなったけど、読み取った値をどう解釈すればいいのかイマイチ分からないなぁ…
ここからは、安定余裕の物理的な意味を考えることで、直感的イメージを深めていきましょう。
そもそもなぜ安定性に余裕が必要かというと、数式モデルに誤差が含まれるためでしたね。
逆に考えると、安定余裕は「どれほどの誤差までなら、システムが内部安定性を保っていられるか」を示す指標であるとも解釈できます。
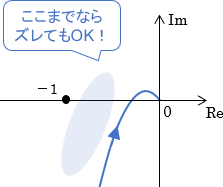

ここからは、ゲイン余裕・位相余裕がどのような誤差を表しているのかを、具体的に説明していきましょう。
※安定余裕で用いるのは開ループ伝達関数であったので、ここで言う「誤差」は「開ループ伝達関数の誤差」を意味します
ゲイン余裕のイメージ
繰り返しになりますが、ゲイン余裕は「位相そのままでゲインをあと何倍できるか」でしたね。
「位相そのままでゲインを定数倍する」という操作は、数式上は「数式モデルに定数ゲインをかける」という操作に等しくなります。
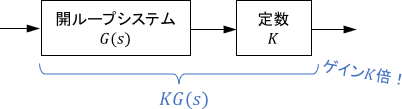

よって、ゲイン余裕は「数式モデル何倍相当の誤差までなら、システムが内部安定性を保っていられるか」であるとイメージすればOKです。
例えばゲイン余裕が$M_G$倍であれば、「開ループ伝達関数が$M_G$倍されるレベルの誤差までなら許容される」ということになりますね。


位相余裕のイメージ
位相余裕は、「ゲインそのままで位相があと何度遅れられるか」でした。
よって先ほどと同様に考えると、位相余裕は「位相遅れ何度相当の誤差までなら、システムが内部安定性を保っていられるか」であるとイメージできます。
例えば位相余裕が$M_\phi$[°]であれば、「開ループシステムの位相が一律に$M_\phi$[°]遅れるレベルの誤差までなら許容される」というわけですね。

とはいえ、「位相が$M_\phi$[°]遅れる」と言われても、遅れ量を直感的にイメージしにくいですよね。なので、遅れ量の単位を[秒]に変換してみましょう。
位相は「信号の波1個分の長さを360°としたときに、信号のズレが何度分になるか」を表すものでした。よって例えば$M_\phi$[°]の位相遅れは、次式で[秒]に変換できることになります。
$$位相M_\phi[°]に相当する遅れ量=\frac{2\pi}{\omega}\cdot\frac{\phi}{360}\ [秒]$$


※$\omega$は信号の角周波数です。角周波数のイメージや、波の長さ(周期)との関係性については、こちらのページをご覧ください
例えばゲイン交差周波数$\omega_G$の信号に対して許容される遅れは、次式で求められるわけですね。
$$\omega_Gに対して許容される遅れ量=\frac{2\pi}{\omega_G}\cdot\frac{\phi}{360}\ [秒]$$
ゲイン交差周波数は「ゲインが0dBになる周波数」であったので、「開ループシステムがギリギリ信号を減衰させずについていけるスピード」を表していることになります。
よって上式は、「システムにとってシビアなスピードでどれだけの遅れが許されるか」という(ちょっとは)直感的に分かりやすい1つの指標として使えることになります。

安定余裕の適正値


ほーん。
で、結局ゲイン余裕と位相余裕はどれくらいあればOKなの?
安定余裕の適正値は、制御目的・数式モデルの精度・システムの性質などに応じて大きく変わります。
よって「これだけあればOK」という絶対的な値はなく、対象システムに応じてケースバイケースで判断する必要があります。
とはいえ大体のイメージは持っておきたいと思うので、教科書などでよく挙げられている参考値を紹介しておきましょう。
| 制御の種類 | ゲイン余裕 | 位相余裕 |
|---|---|---|
| 定値制御 | 3~10dB(約1.4~3.2倍) | 20°以上 |
| 追従制御 | 10~20dB(約3.2~10倍) | 40~60°以上 |

例えば定値制御の場合は、ゲイン余裕が2,3倍レベルなので、「ゲイン2,3倍レベルの誤差に対して安定性を保てればOK」ということになります。
一方の追従制御では、ゲイン2,3倍程度の余裕では不十分であることが分かります。激しい目標値変化に対応するために、さらに大きな余裕が必要というわけですね。
繰り返しになりますが、これらはあくまで参考値です。
一般的に安定余裕を大きく取ると、入力をパワフルに使った攻めの制御ではなく、なるべく危ないことはしないように入力を絞る守りの制御になりがちです。よって、上の参考値を律儀に守っていると、制御が保守的になりすぎて、制御性能が犠牲になることも多々あるでしょう。


自身のシステムがどれくらいの安定余裕を持つべきなのかは、制御目的・数式モデルの精度・システムの性質などに基づいて個別に検討するようにしましょう。
以上、安定余裕の意味・直感的イメージ・読み取り方についての解説でした!
- 安定余裕は「フィードバック制御システムが内部安定だとしたときに、それがどれくらい安定であるか」を示す指標
- 安定余裕からは「数式モデルの誤差がどれほどまでなら許容されるか」が分かる
- ゲイン余裕は「ゲイン何倍相当の誤差までなら許容されるか」を表す
- 位相余裕は「位相何度相当の誤差までなら許容されるか」を表す







コメント
系が不安定になるときは外力(ここでは入力u)が系に対して仕事をしている場合だと思うのですが,ここでの位相余裕やゲイン余裕との対応関係が分かりません.
例えば,位相が180°遅れると仕事率=速度・力(・は内積)が正になったりするのかとも思いましたが上手くいきません.
前提条件が分からないのでなんとも言えませんが、例えば入力uが力、出力yが位置である機械システムの場合は「十分な時間がたった後に、制御器が生み出す入力uによって制御対象の内部エネルギーが発散するかどうか」という条件に対応すると思われます。
想定されている「入力uが系に対して仕事をしている」という条件との主な違いは、次のような「いい仕事」と「悪い仕事」を適切に考慮できるかどうかです。
制御工学で扱うのは動的システムなので、ある時刻で信号がどうなっているかではなく、「無限の時間がたった後に信号がどうなっているのか」という観点での条件になっていると解釈すればわかりやすいかもしれません。
返信ありがとうございます.
想定している系はそのようなものです.
「十分な時間がたった後に、制御器が生み出す入力uによって制御対象の内部エネルギーが発散するかどうか」というところは分かったのですが,やはり位相遅れとの関係が分かりません.
積分結果ということなので,直観的にイメージできるものでもないのでしょうか?
「数式は理解したけど、それが現実の現象として何を意味するのかをイメージしたい」ということですよね…。自分も同じタイプなのでよく分かります。
例えば最初のコメントで示唆されていた「位相が180°遅れると何が起きるのか」という問いに対しては、こちらのページが解答の根っこになると思います(既に見てくださっているかもしれませんが)。
上記ページは動力学的な観点の説明ではなく、一段階抽象化した「システムと信号」という観点での説明ですが、出力yを位置だと思えば「位置信号がフィードバックループを回るたびに増幅されてしまうような『悪い入力u』が生まれている」というイメージには繋がると思います。
「そうではなく、当初の『仕事とエネルギーの観点』でイメージしたい」ということであれば、制御器&制御対象を何か具体的に設定して、上記イメージをもう一段階噛み砕く必要がありますね…。これはやったことがないので具体的イメージに繋がるかどうかは分かりませんが、制御ループを考える以上、動力学的な観点だけではどうしても議論を進めにくくなるので、結局上記のようなイメージに帰着する気もします。
求めている回答をズパッと出せずすみません。何かいいイメージが思いついたら追ってコメントさせていただきます。
該当ページ拝見いたしました.
閉ループを回っているうちに増幅されるイメージは付きましたが,仕事での解釈はなかなか難しそうですね,,,
わたしも,たまに考えてみます.
ありがとうございます.