角周波数（角振動数）とは？分かりやすいイメージで楽々マスター！

角周波数（角振動数）は物理学や制御工学でよくでてきますが、慣れていないと解釈に苦労しがちです。このページでは、角周波数の直感的意味と使い方を解説します。

周波数のおさらい

角周波数の話に入る前に、ベースとなる周波数についておさらいしておきましょう。既にご存じの方は、読み流してください。

周波数は、振動の速さを表す物理量で、主に$f$で表されます。より具体的には「1秒に何回振動するか」を表すものです。光・音・電気・機械など、様々な振動現象を表すのに使用されます。

周波数の単位はHz（ヘルツ）です。例えば1Hzの波は1秒に1回振動しますし、3Hzの波は1秒に3回振動します。

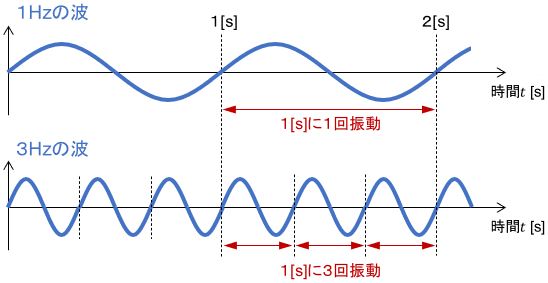
「1秒の中に波が何個入っているか」とも解釈できますね。よって、周波数から振動の周期を逆算することもできます。

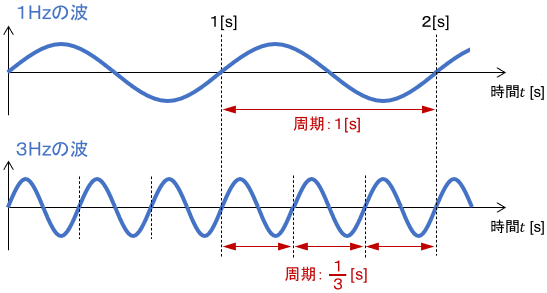
より一般化すると、$f$[Hz]の振動の周期$T$[s]は次のように計算できます。

$$T=\frac{1}{f}$$

同様に、振動の周期$T$から周波数$f$を計算することもできますね。

$$f=\frac{1}{T}$$

周期の逆数が周波数となるので、周波数の単位[Hz]は[1/s]と等価です。「1秒あたりの振動回数」という意味そのままの単位だと解釈できます。

角周波数とは？

それでは本題に入りましょう。角周波数は様々な解釈が可能ですが、ここでは物理学・制御工学の実用シーンにて役に立つ解釈を紹介します。

角周波数を一言で表すと、「振動をsin関数で表す際によくでてくる係数をまとめたもの」です。具体的には、周波数$f$に$2\pi$をかけた、$2\pi f$が角周波数となります。

$$角周波数\ \omega = 2\pi f$$

なぜこのようになるのかを、詳しく見ていきましょう。

1Hzの波をsin関数で表してみる

1Hzの波をsin関数で表すことを考えましょう。まずはsin関数そのものの性質を見てみます。素のsin関数$\sin x$をプロットすると、次のようになります。

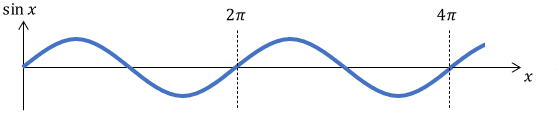
生身のsin関数は$2 \pi$ごとに1回振動していますね。ということは、周波数を1Hzにするには、1秒ごとにsin関数に$2 \pi$をぶちこめばよさそうです。

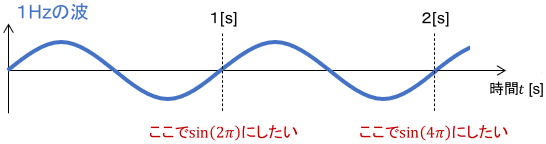
よって1Hzのsin波を数式で表すと、次のようになりますね。

$$1\mathrm{Hz}の\sin 波=\sin \left( 2 \pi \cdot t \right)$$

3Hzの波をsin関数で表してみる

今度は3Hzのsin波を考えてみましょう。1秒に3回振動させたいので、1秒ごとにsin関数に$2 \pi$を3つぶちこめばよいですね。

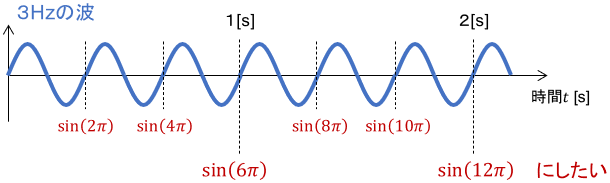
よって3Hzのsin波を数式で表すと、次のようになります。

$$3\mathrm{Hz}の\sin 波=\sin \left( 2 \pi \cdot 3 \cdot t \right)$$

一般化すると角周波数が現れる！

より一般化して、$f$[Hz]のsin波を考えましょう。1秒に$f$回振動させたいので、1秒ごとにsin関数に$2 \pi$を$f$個ぶちこむと完成ですね！

$$f\mathrm{[Hz]}の\sin 波= \sin \left( 2 \pi f \cdot t \right)$$

ということで、物理学や制御工学で$f$[Hz]の振動を扱う際は、式の中にコレがおびただしいほど出てきます。そのたびにいちいち$\sin \left( 2 \pi f \cdot t \right)$と書くのは面倒ですよね。

結局$2\pi f$の部分は定数なので、それを$\omega$と1つの文字で表してしまいましょう。この$\omega$が角周波数です。

$$\begin{gather}角周波数\ \omega = 2\pi f \\\\ \sin \left( 2 \pi f \cdot t \right) = \usg{\sin \left( \omega t \right)}{スッキリ！} \end{gather}$$

直感的には、角周波数は「1秒あたり何ラジアンの角度がsin関数にぶちこまれるか」を表す物理量となっています。ここまでの例の通り、実際には1秒あたり$2\pi$[rad]が$f$回、つまり$2\pi f$[rad]がぶちこまれるわけですね。

よって、角周波数の単位は[rad/s]です。上記直感的イメージそのままの単位となっていますね。

角周波数の各種公式

最後に、角周波数を使うにあたって知っておきたい公式を紹介しておきます。とはいえ、ここまでの話をふまえると当たり前のことばかりです。

まず、角周波数$\omega$から普通の周波数$f$を求める式です。

$$f = \frac{\omega}{2\pi}$$

1秒あたり$2\pi$が$f$回ぶちこまれるのが角周波数なので、それを$2\pi$で割ると周波数$f$になるわけですね。角周波数の定義式からも明らかです。

次に、角周波数から振動周期を求める式です

$$T = \frac{2\pi}{\omega}$$

周期は周波数の逆数なので、先ほどの式をひっくり返すだけですね。

これらの公式は、暗記するよりも角周波数の意味を理解して、自力ですぐに導出できるようにしておくことが重要です。

以上、角周波数の直感的意味と使い方についての解説でした！