超分かるテイラー展開。イメージ・意味・使い方を具体例で解説！

関数を次の形で展開することを、テイラー展開と呼びます。

$$f(x) = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3 + \cdots$$

・・・お、おう

って感じですよね。

一見無機質に見えるこの式も、意味を理解すれば非常に納得のいく形をしていることが分かります。このページでは、テイラー展開の直感的イメージ・式の意味・使い方について詳しく解説していきます。

テイラー展開とは

テイラー展開の超概要

テイラー展開は、次のように関数を多項式の形に展開（変換）する手法です。

$$f(x) = k_0 + k_1 (x-a) + k_2 (x-a)^2 + k_3 (x-a)^3 + \cdots$$

$k_0,k_1,\ldots$ と $a$は定数です。このように展開された形のことを、テイラー級数と呼びます。「関数をテイラー級数に展開すること」を「テイラー展開」と呼ぶわけですね。

上の式は$(x-a)$で整理していますが、展開すると結局このようにシンプルな多項式になります。

$$f(x) = K_0 + K_1 x + K_2 x^2 + K_3 x^3 + \cdots$$

$K_0,K_1,\ldots$ は展開結果をまとめた定数です。$(x-a)$で整理したほうが数式に法則性が現れスッキリまとまるので、以降は$(x-a)$で整理した形をベースにお話します。

テイラー級数近似

実際は無限に項を計算し続けるわけにはいかないので、どこかで計算を打ち切る必要があります。このとき、計算した部分は関数$f(x)$の近似式となり、計算しなかった残りの部分が近似の誤差となります。

$$f(x) = \ubg{k_0 + k_1 (x-a) + k_2 (x-a)^2}{ココだけ計算する} +\ubg{k_3 (x-a)^3 + \cdots}{ココから先は誤差} $$

$$近似式： f(x) \approx k_0 + k_1 (x-a) + k_2 (x-a)^2$$

このような関数の近似は、「テイラー級数近似」と呼ばれます。「テイラー級数による近似」「テイラー展開による近似」とも呼ばれます。

当然、考慮する項数が多いほど、つまり多項式の次数が上がるほど近似の精度もよくなっていきます。考慮した項の数に応じて、0次近似、1次近似、2次近似・・・と呼びます。

$$\begin{align} &0次近似（定数）&&：&&f(x)\approx k_0\\&1次近似（直線）&&：&&f(x)\approx k_0 + k_1 (x-a)\\&2次近似（2次関数）&&：&& f(x)\approx k_0 + k_1 (x-a) + k_2 (x-a)^2\end{align}$$

係数の考え方

当然、それぞれの係数$k_0,k_1,\ldots$ をどのように選ぶかがキーとなるわけですが、テイラー展開では$x$軸上のある点$a$を基準に、その近傍でなるべく精度が高くなるように係数を決定します。

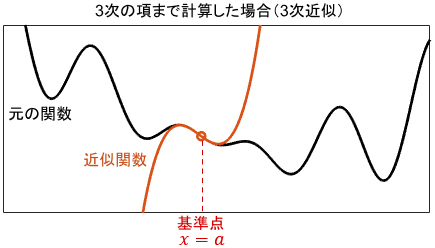
より具体的には、基準点$x=a$において、展開式の1階微分値、2階微分値、3階微分値…が元の関数と等しくなるように係数を設定します。その結果、次のような複雑なテイラー展開の式になるというわけです。

$$f(x) = \ubg{f(a)}{k_0} + \ubg{f^{\prime}(a)}{k_1} (x-a) + \ubg{\frac{f^{\prime \prime}(a)}{2!}}{k_2} (x-a)^2 + \ubg{\frac{f^{\prime \prime \prime}(a)}{3!}}{k_3} (x-a)^3 + \cdots$$

複雑な形をしていますが「結局$(x-a)$以外の部分はただの係数だ！」と思うと、ちょっと簡単に見えてくるのではないでしょうか。（なぜ係数がこんな形になっているのかは、後ほど詳しく説明します）

当然、基準点をどこに取るかによって、展開結果は変わってきます。基準点$x=a$に対してテイラー展開することを「$x=a$まわりでテイラー展開する」とか「$a$まわりでテイラー展開する」と言います。特に、$x=0$まわりでのテイラー展開は、マクローリン展開と呼ばれます。

テイラー展開の使い道と具体例

ほーん。で、このテイラー展開って何に使えるの？

テイラー展開が役に立つのは、「ちょっと誤差があってもよいので、基準点近傍で関数を単純化したい」という場面です。具体例を見ながら、そのイメージと利点を直感的に理解していきましょう。

指数関数のテイラー展開例

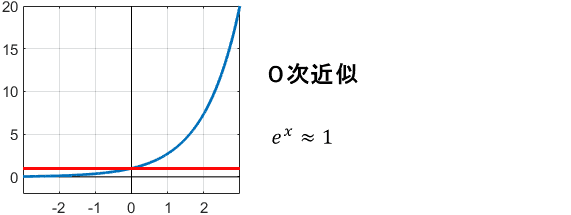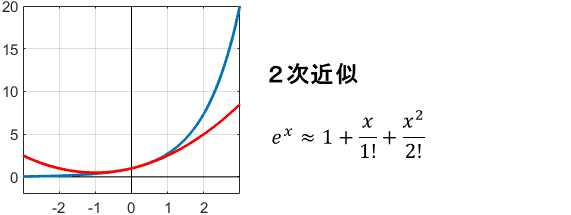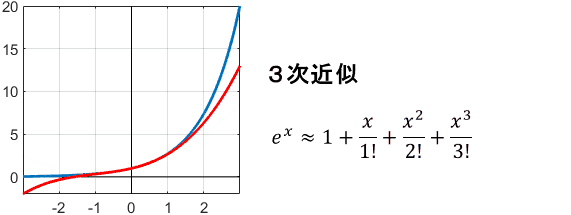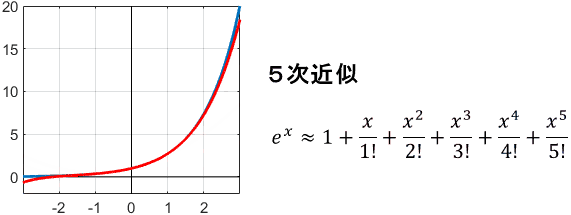
指数関数の代表である$e^x$を$x=0$まわりでテイラー展開（つまりマクローリン展開）すると、次のようになります。

$$e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!}+ \cdots$$

これを用いて、$e^x$をテイラー級数近似してみましょう。項の数、つまり次数を増やしていくと、次のような近似結果が得られます。

最初は雑な近似ですが、次数が上がるにつれて、$x=0$まわりで元の関数にフィットしていってますね。これで、テイラー級数近似のイメージは大体つかめたかと思います。

sin関数のテイラー展開例

sin関数を$x=0$まわりでテイラー展開（つまりマクローリン展開）すると、次のようになります。

$$\sin x = x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!} + \frac{x^9}{9!} – \cdots$$

1次、3次、5次…と、奇数次の項だけで展開されていますね。これを用いてテイラー級数近似すると、次のようになります。

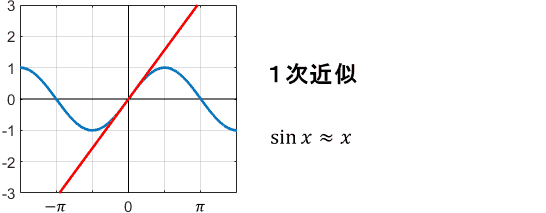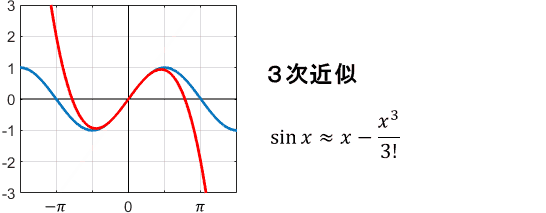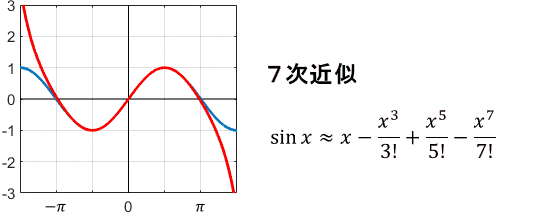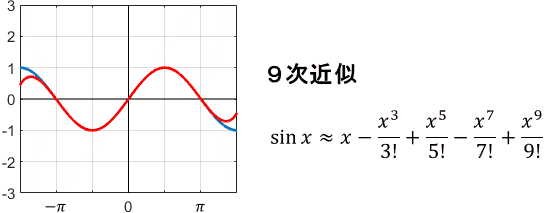
やはり次数が上がるほど、$x=0$まわりで近似精度が上がっていますね。特に、sin関数の1次近似（＝線形近似）は非常によく使われます。

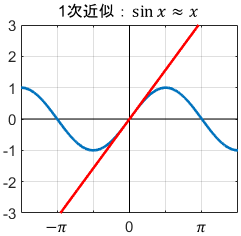
理由は簡単で、sin関数は様々な分野で非常に多く登場するわりに、扱いにくいからです。$\sin x$がただの$x$になると嬉しいですよね。上の図を見ると、$x=0$近傍でしかsin関数を使わないのであれば、$\sin x \approx x$と簡単にしても誤差が少ないことが分かります。

メジャーな例は振り子の運動方程式です。これにはsin関数が含まれるので手計算で解くのは難しいですが、振り子の角度が十分小さいとして$\sin \theta \approx \theta$という近似を適用すると、式が簡単になり手計算で解けるようになります。

このように、関数を単純化させることで複雑な式の計算を可能にするのが、テイラー展開の主な使いみちです。特に直線は数学的に非常に扱いやすいため、1次近似（線形近似）はぶっちぎりでよく使われます。どんな関数でも超拡大したら直線に見えますからね。

ついでに、sin関数の1次近似がどの角度まで使えるのか詳しく見てみましょう。角度が小さい範囲での1次近似を拡大したものがこちらです。（分かりやすいように、横軸の単位を度に変更しています）

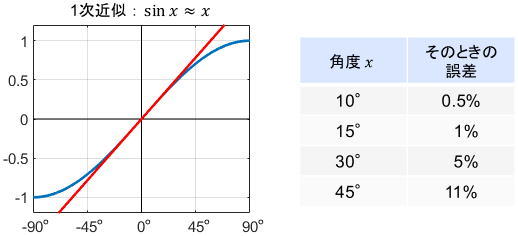
もちろん用途にもよりますが、±10°以内であればほとんど誤差なく使えそうですね。

cos関数のテイラー展開例

cos関数を$x=0$まわりでテイラー展開（つまりマクローリン展開）すると、次のようになります。

$$\cos x = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \frac{x^6}{6!} + \frac{x^8}{8!} – \cdots$$

0次、2次、4次…と、偶数次の項だけで展開されています。これを用いてテイラー級数近似すると、次のようになります。

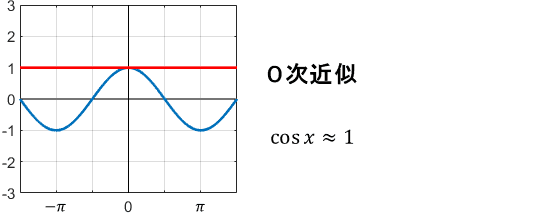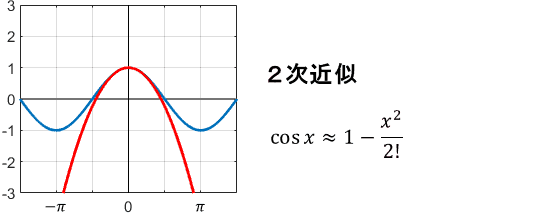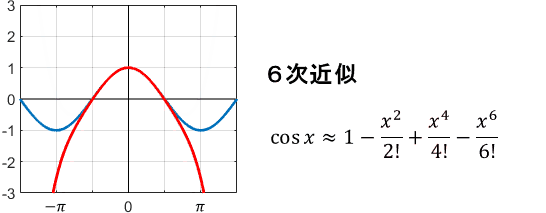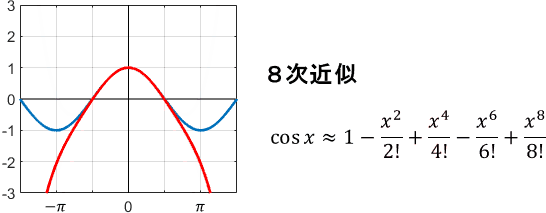
cos関数はsin関数を横にずらした形をしているので、実質的には先ほどの例と基準点が変わっているだけですね。ただ、近似の様子は結構変わっています。

特にcos関数の直線近似（0次近似）は、sin関数と異なりヒドいですね…

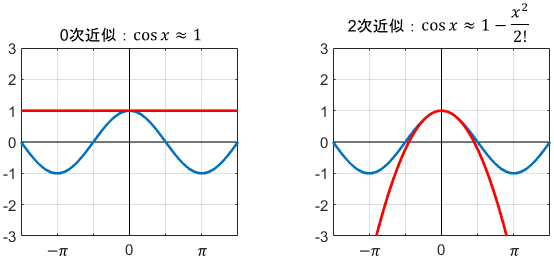
2次近似は結構よさそうですが、ほとんど使われません。2次関数もcos関数も扱いやすさはあまり変わらず、近似するメリットがほとんどないからです。やはり直線の扱いやすさは偉大ですね。

このようにテイラー級数近似は、関数や基準点によって近似の精度が大きく変わります。適用する関数のイメージをしっかり持った上で使用するのが重要です。

テイラー展開の式の意味

ほーん。イメージは分かったけど、なんでそれがこんな式になるの？

それでは、テイラー展開がなぜこのような複雑な式になるのか、詳しく見ていきましょう。

$$f(x) = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3 + \cdots$$

お気付きの通り、各項には法則性がありますね。$n$次の項は、次のように表されます。

$$\ubg{\frac{f^{(n)}(a)}{n!}}{ただの係数} (x-a)^n$$

この係数は、基準点$x=a$において、式の1階微分値、2階微分値、3階微分値…が元の関数と等しくなるように設定されているんでした。各項がこのような形になる理由を、次のような関数のテイラー級数近似を考えながら、確認していきましょう。

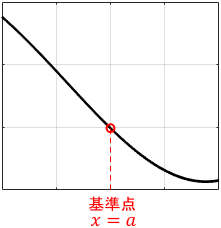
以降、元の関数$f(x)$と区別するために、近似後の関数を$\tilde{f}(x)$と表します。

$$f(x) \approx \tilde{f}(x)$$

それでは、テイラー級数近似の項を1つずつ増やしながら、順を追って説明していきましょう。

0次の項まで（0次近似）

まず、テイラー展開最初の項です。

$$\tilde{f}(x) = \ubg{f(a)}{0次の項} $$

超乱暴ですが、関数をある一定の値で表現しようとしているわけですね。当然、基準点$x=a$における関数の値$f(a)$を用いることになります。

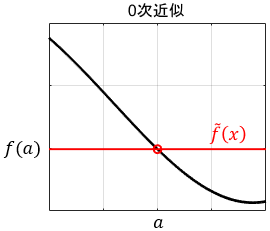
さすがにちょっと雑すぎですね…。さらに項を追加して、精度を高めていきましょう。

1次の項まで（1次近似）

項を１つ増やしてみます。

$$\tilde{f}(x) = f(a) + \ubg{f^{\prime}(a)(x-a)}{1次の項} $$

1次の項が増え、直線になりました。これは基準点$x=a$にて元の関数$f(x)$と同じ値・同じ傾きを持つ直線の式ですね。数式で表すと、次の特性を持っています。

$$\begin{align}近似関数\quad \tilde{f}(a) &= f(a) \\1階微分\quad \tilde{f}^{\prime}(a) &= f^{\prime}(a) \end{align}$$

一言でいうと、基準点における$f(x)$の接線ですね！

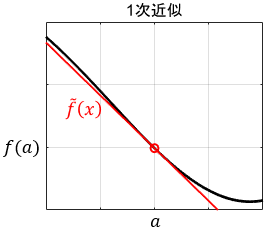
式の形をより直感的に解釈してみましょう。今、新しく増やした1次の項は次のような働きをしていることが分かります。

このように、新しく増やした項を必要なときにだけ作用させるために、テイラー展開の式は$(x-a)$に基づいたものになっていると言えます。

$(x-a)$は「$a$から見た$x$の位置」を表しているため、まさしく$x=a$を「基準」としてそこからの距離に応じて誤差を補正する表現になっているわけですね。

とはいえ、まだ雑な感じが否めませんよね。$x=a$の超近傍でしか$f(x)$を使わないのであれば、これで十分かもしれませんが…。もっと項数を増やして、1次近似の誤差をさらに補正していきましょう。

2次の項まで（2次近似）

$$\tilde{f}(x) = f(a) + f^{\prime}(a)(x-a) + \ubg{\frac{f^{\prime \prime}(a)}{2!}(x-a)^2}{2次の項} $$

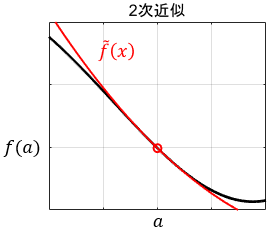
2次関数になり、さっきよりも精度が向上していますね。新しい2次の項で、1次近似の誤差をさらに補正しているわけですが、数式上ではどのように解釈すればよいでしょうか？

1次近似の問題は、傾き一定の直線しか表現できないことですね。本当はもうちょっと線をググッと曲げてフィットさせたいわけです。

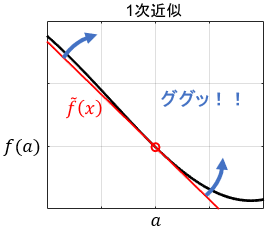
直線を曲げるには、「傾きの変化率」、すなわち2階微分を考えればよいでしょう。2次の項を追加したおかげで、近似関数$\tilde{f}(x)$の2階微分が0ではなくなりました。これを計算してみましょう。

$$\begin{align} 近似関数\quad \tilde{f}(x) &= f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2\\ 1階微分\quad \tilde{f}^{\prime}(x)&= f^{\prime}(a) + f^{\prime \prime}(a)(x-a) \\[3pt] 2階微分\quad \tilde{f}^{\prime \prime}(x)&= f^{\prime \prime}(a)\end{align}$$

2階微分が$f^{\prime \prime}(a)$になりましたね。上式にそれぞれ$x=a$を代入すると、近似関数は基準点にて次の性質を持つことが分かります。

$$\begin{align}近似関数\quad \tilde{f}(a) &= f(a) \\[3pt]1階微分\quad \tilde{f}^{\prime}(a)&= f^{\prime}(a) \\[3pt]2階微分\quad \tilde{f}^{\prime \prime}(a)&= f^{\prime \prime}(a)\end{align}$$

つまり、近似した2次関数$\tilde{f}(x)$は基準点$x=a$にて元の関数$f(x)$と同じ値・同じ傾き・同じ「傾きの変化率」を持つというわけですね。

ここで注目したいのは、新たに追加した2次の項が、基準点$x=a$にてこれまで作った他の項の作用を邪魔しないようになっている点です。先ほどと同様に2次の項の働きをまとめると、次のようになっていますよね。

これらが実現できているのは、やはり式が$(x-a)$に基づいた表現になっているためです。このおかげで、$x=a$にて不要な項が全て0になってくれているというわけですね。

ただやはり、基準点を離れるとちょっと曲がりすぎになり、精度が低下しています。3次の項を増やして、この誤差をさらに補正してみましょう。

3次の項まで（3次近似）

$$\tilde{f}(x) = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \ubg{\frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3}{3次の項} $$

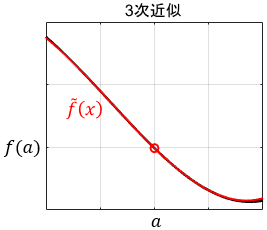
3次関数になり、さらに精度がよくなりましたね。式は複雑になってますが、基本的な考え方は2次の項と同じなので、ササッと読み進めてOKです。ただ、後半に新たな発見があります。

2次近似の限界は「傾きの変化率」が一定であることなので、「傾きの変化率の変化率」、すなわち3階微分を考えます。

$$\begin{align}近似関数\quad \tilde{f}(x) &= f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3 \\[1pt]1階微分\quad \tilde{f}^{\prime}(x) &= f^{\prime}(a) + f^{\prime \prime}(a)(x-a) + \frac{f^{\prime \prime \prime}(a)}{2!}(x-a)^2 \\[3pt] 2階微分\quad \tilde{f}^{\prime \prime}(x) &= f^{\prime \prime}(a) + f^{\prime \prime \prime}(a)(x-a) \\[6pt]3階微分\quad \tilde{f}^{\prime \prime \prime}(x) &= f^{\prime \prime \prime}(a) \end{align}$$

3階微分が$f^{\prime \prime \prime}(a)$になりましたね。上式にそれぞれ$x=a$を代入すると、近似関数は基準点にて次の性質を持つことが分かります。

$$\begin{align}近似関数\quad \tilde{f}(a) &= f(a) \\[3pt]1階微分\quad \tilde{f}^{\prime}(a)&= f^{\prime}(a) \\[3pt]2階微分\quad \tilde{f}^{\prime \prime}(a)&= f^{\prime \prime}(a) \\[3pt]3階微分\quad \tilde{f}^{\prime \prime \prime}(a)&= f^{\prime \prime \prime}(a)\end{align}$$

つまり、近似した3次関数$\tilde{f}(x)$は基準点$x=a$にて元の関数$f(x)$と同じ値・同じ傾き・同じ「傾きの変化率」・同じ「傾きの変化率の変化率」を持つというわけですね。

$(x-a)$に基づいた表現により、新たに追加した3次の項が、基準点$x=a$にてこれまで作った他の項の作用を邪魔しないようになっているのも、2次の場合と同じですね。

ここで新たに注目してほしいのは、近似関数$\tilde{f}(x)$を微分していく際、どんどん前にでてくる$(x-a)$の右肩の係数が、階乗にキレイに打ち消されていることです。例えば3次の項を3階微分するときは、以下のように次々と係数が打ち消され、最後に$f^{\prime \prime \prime}(a)$だけが残りますよね。

テイラー展開に登場する謎のビックリマークは、このためにあったわけですね！

n次の項まで（n次近似）

ここまでくれば、後は全く同じ考え方で式を拡張できます。$n$次の項は、次のように表すことができます。

$$f(x) = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \cdots + \ubg{\frac{f^{(n)}(a)}{n!}(x-a)^n}{n次の項} $$

考え方は、次の通りです。これまでのまとめですね。

そして、これを延々と並べたものがテイラー展開の式となります。

$$f(x) = f(a) + f^{\prime}(a)(x-a) + \frac{f^{\prime \prime}(a)}{2!}(x-a)^2 + \frac{f^{\prime \prime \prime}(a)}{3!}(x-a)^3 + \cdots$$

基準点を$a=0$とすると、マクローリン展開の式となりますね。

$$f(x) = f(0) + f^{\prime}(0)x + \frac{f^{\prime \prime}(0)}{2!}x^2 + \frac{f^{\prime \prime \prime}(0)}{3!}x^3 + \cdots $$

以上、お疲れさまでした。テイラー展開の直感的イメージ・式の意味・使い方の解説でした。

初見では面食らう複雑な式も、その意味を理解すれば自然に覚えられると思います。今後、手に負えない複雑な式を解析する必要が出た場合は、是非テイラー級数近似で単純化してみてくださいね！