片対数グラフ・両対数グラフとは？読み方・書き方・使い方を解説！

対数グラフを初めて見たとき、こう思った方も多いのではないでしょうか。

なにこれ？どう読むの？何の役に立つの？

このページでは、そんな疑問を解消するために、対数グラフの読み方・書き方と使い所を具体例を交えて説明します。

対数グラフ超概要

対数グラフは倍々グラフだ！

対数グラフは目盛りごとに値が倍々で増えていくグラフです。

最も使用頻度の高い常用対数グラフを例に説明します。普通の目盛りと対数目盛りを比較してみましょう。

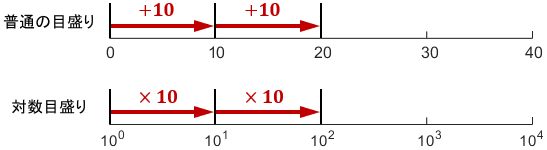
普通の目盛りは一定距離ごとに数が10ずつ増えていますが、対数目盛りは一定距離ごとに数が10倍ずつ増えています。ちょうど目盛りを「一、十、百、千、万…」と読んでいくイメージですね。

対数グラフの種類

対数目盛りがx軸・y軸のどちらかに付いているものを片対数グラフ、両方に付いているものを両対数グラフといいます。

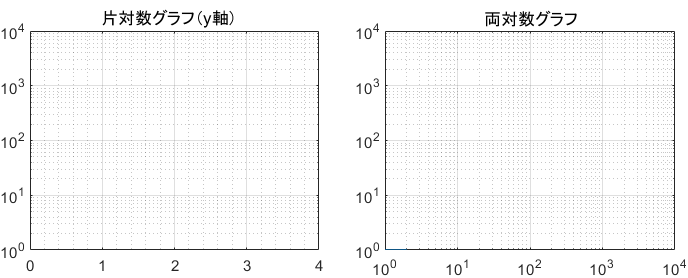
対数軸は何だか目盛りが偏っていて、読み方がよく分かりませんね…。詳しい読み方は後で説明するので、今は細かい目盛りは無視して「倍々」のイメージだけしっかり抑えておけばOKです。

対数グラフの使い所

対数グラフの読み方に入る前に、まずは対数グラフの使い所を抑えておきましょう。（そのほうが理解しやすくなるので）

対数グラフは、様々なオーダー（桁数）のデータをざっくりと確認・比較したいときに非常に便利です。以下の具体例を見ると、どういうことかすぐに分かると思います。

y軸片対数グラフの例

例えば、4つの産業分野A,B,C,Dの、 1950年～2000年における市場規模をグラフで比較したいとします。これらのデータを普通のグラフでプロットした結果がこちらです。

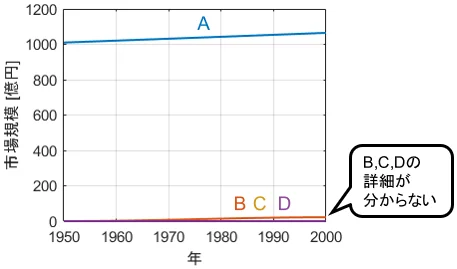
産業Aの市場規模が圧倒的ですね。ただこれでは他の産業の規模や大小が全く分かりません。産業B,C,Dのデータにズームインしてみましょう。

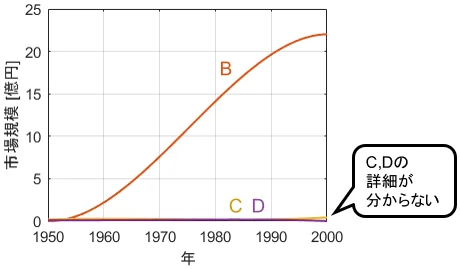
なるほど、産業Bは50年で順調に成長したようです。ただ、また同じ問題が生じていますね。産業C,Dの詳細が全く分かりません。さらにズームインしてみましょう。

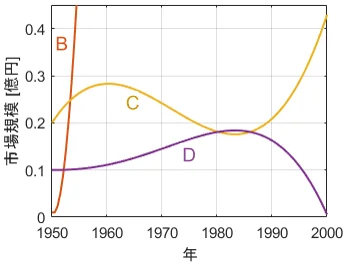
これでようやく全体像が見えました。大規模に見えた産業Bも、1950年初頭は産業C,Dより規模が小さかったようです。また、1980年あたりで産業Cと産業Dの市場規模がほぼ同じになっていますね。

このように、普通のグラフでは、オーダーの大きなデータのせいでオーダーの小さなデータがつぶれてしまうという問題があります。

対数グラフを用いると、この問題が一発で解決します。y軸を対数目盛にしてプロットした結果がこちらです。

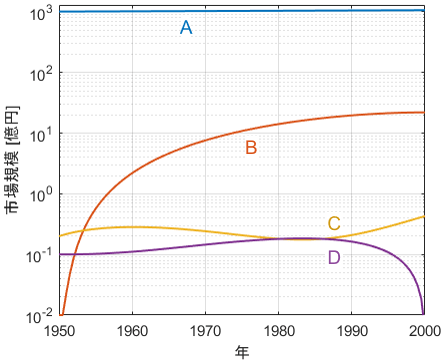
産業Aが1000億オーダーの規模であること、産業Bが10億オーダーの規模であること、産業C,Dが1000万オーダーの規模であることが分かります。さらに、産業Bは最初は他より規模が小さかったことや、1980年あたりで産業Cと産業Dの規模がほぼ同じになっていることも、一目瞭然でわかりますね！

このように、詳細な値は置いといて、様々なオーダーのデータをざっくりと確認・比較したいときに非常に便利なのが対数グラフです。

x軸片対数グラフの例

こちらも、基本の考え方は同じです。様々なオーダーのx軸値に対して結果を確認・比較したいときに使用します。

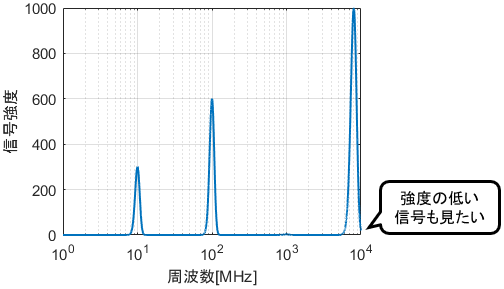
例えば、ある機械が発する電波の信号強度を調べたいとします。それぞれの電波周波数に対する信号強度を普通のグラフでプロットした結果がこちらです。

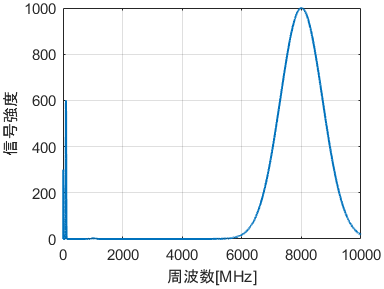
8000MHzあたりで強い信号が検出されていますね。左のほうにも何やら信号が検出されていますが、潰れて詳細が分かりません。

もうお分かりですね。 x軸を対数目盛にしてプロットした結果がこちらです。

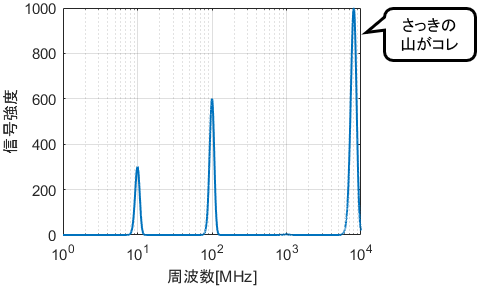
10MHz・100MHzあたりにも信号があることが分かりました。

このように、x軸を対数にすることで様々なオーダーのx軸値に対する結果を一目で確認できるようになります。

両対数グラフの例

両対数グラフはこれまでの組み合わせです。

例えば先ほどの信号検出の例では、強度が約100～1000の信号のみを確認しました。ここで、強度10以下の信号についても傾向を見たいとしましょう。

この場合は、最初の例と同じくy軸も対数目盛にすればよいですね。そうすれば、両対数グラフの出来上がりです。同じデータを両対数グラフでプロットした結果がこちらです。

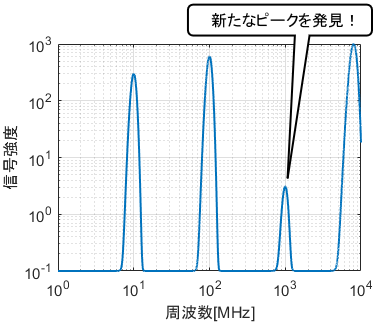
新たに、1000MHzあたりにも小さな信号ピークがあることが分かりました。

このように、x軸・y軸ともに様々なオーダーを取り扱えるのが両対数グラフです。

対数グラフの詳しい読み方

それでは、いよいよ対数グラフの詳しい読み方を見ていきましょう。あの偏った目盛りはどのように読むのでしょうか？

分かりやすくするため、対数目盛りに値を記入しました。以下、これを用いて説明します。

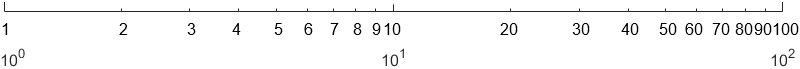
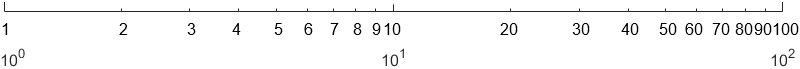
どこでも成り立つ倍々関係

対数目盛は「倍々」で値が増えていくので、1と2の間の距離は「2倍」を表すはずです。

この「2倍の距離」を目盛りの様々な所に当ててみると、確かにどこでも2倍が成り立つことが分かります。

2倍だけでなく、他の倍率の距離と組み合わせても、きちんと整合性が保たれています。よくできてますねー。

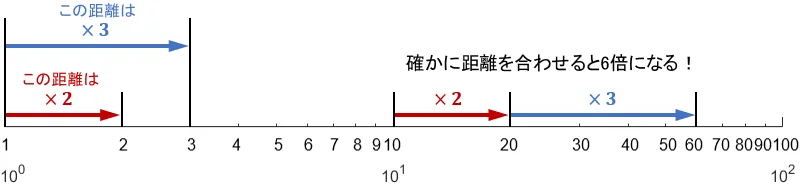
これらの性質を利用すると、目盛りのない場所の値も大体見積もることができます。

左に進むとどうなる？

右に進んで倍になるということは、左に進むと割り算になります。

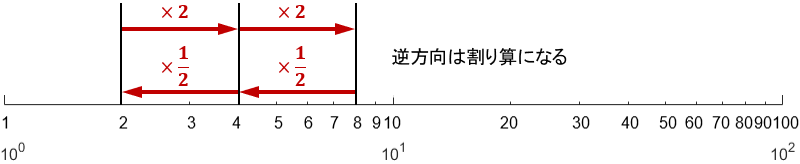
「行って戻ってくると同じ値になる」と考えると当たり前ですね。

よって、対数目盛りには0やマイナスがありません。いくら左に行っても、1/100、1/1000、1/10000…と数が小さくなり、永遠に0にはたどり着けないためです。

ちょうど中間の値は？

1と10のちょうど中間点の値を考えてみましょう。中間の地点は「2回進むと10倍になる距離」と考えると、$10^{\frac{1}{2}}$、つまり$\sqrt{10}$となります。同様に、1/4の地点は $10^{\frac{1}{4}}$ となります。

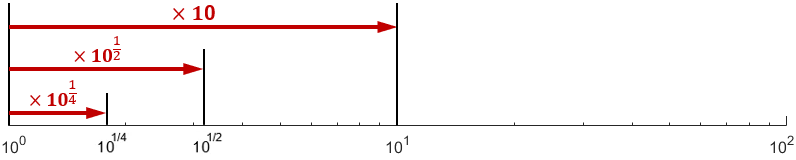
この考え方を応用すると、対数グラフを書くときは、「10を何乗したらその数になるか」、つまり$\log_{10} x$を計算し、その値を（普通の目盛りの感覚で）プロットすればよいことになります。（最近はソフトが自動でデータを対数プロットしてくれるので、このような計算をすることはあまりありませんが）

ここまでくれば、だいぶ対数目盛りに慣れてきたのではないかと思います。

色々な関数を対数グラフで見てみる

最後に、なじみのある関数たちが対数グラフでどのように見えるのかを見てみましょう。これを知っておけば、対数グラフの理解がさらに深まりますよ！

sin関数

最初にsin関数を見ておくとイメージがつかみやすいと思います。

前述の通り、対数グラフはマイナスがプロットできないので、解が全て正になる $\sin x+1$ をプロットしてみましょう。

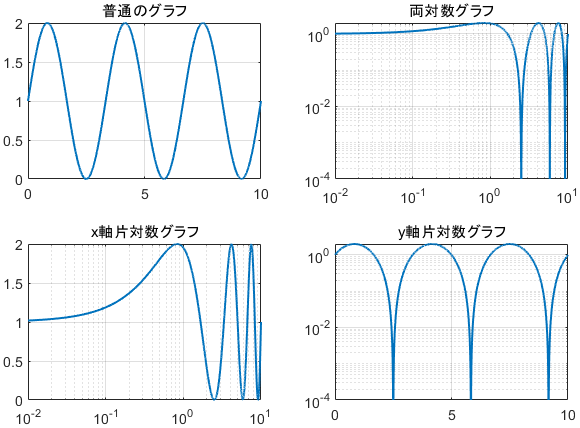
x軸片対数グラフを見ると、sin関数がなんだか右側にギューッと圧縮されていますね。倍々グラフなので、「右に行けば行くほど１目盛りあたりに含まれる数がどんどん増える」と考えると、右に行くほど情報が密になることが納得いくと思います。

y軸片対数グラフも同様に、上側に情報がギューッと圧縮されているわけですが、その結果波がピョコピョコした形になっています。この「ピョコピョコ」は対数グラフで結構見かけるので、「対数グラフのピョコピョコはただの上下振動」と覚えておくと便利です。

両対数グラフはそれぞれの組み合わせになっていますね。

直線

次に、直線を見てみましょう。次の2つをプロットします。

$$\begin{align}y&=x\\y&=2x\end{align}$$

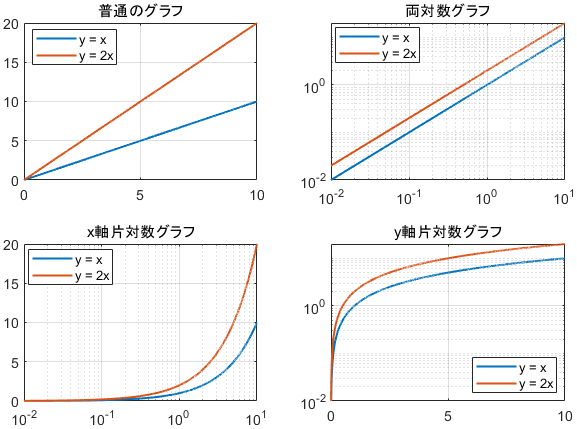
x軸片対数グラフ・y軸片対数グラフでは、先ほどと同じく情報がギューッと圧縮されるために直線が歪んで見えています。

直線は両対数グラフでも直線のままですが、傾きがどちらも同じになっていますね。これは、どちらの関数も次の通り「倍々」の特性は同じであるためです。

• $x$を10倍したら$y$も10倍
• $x$を100倍したら$y$も100倍
• $x$を1000倍したら$y$も1000倍 …

2次関数・3次関数

次はこちらの関数です。

$$\begin{align}y&=x^2\\y&=x^3\end{align}$$

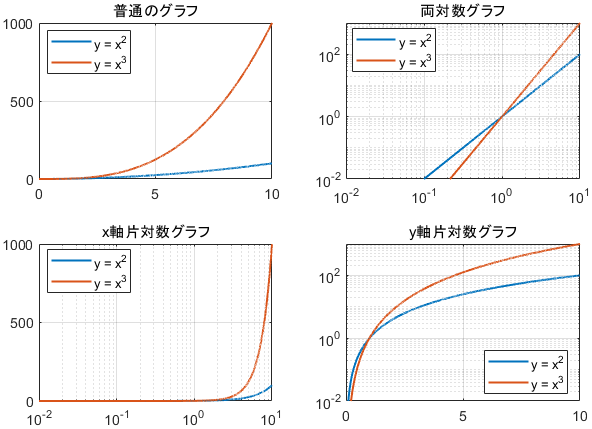
x軸片対数グラフ・y軸片対数グラフは、直線の場合と同様に歪んでいますね。特に言うことはありません。

注目すべきは両対数グラフです。どちらの関数も直線であり、$y=x^3$ のほうが傾きが大きくなっていますね。これは、それぞれの関数が次のような「倍々」の特性を持っているためです。

• $y=x^2$は、$x$を10倍したら$y$は$10^2$倍
• $y=x^3$は、$x$を10倍したら$y$は$10^3$倍

指数関数

どんどん行きましょう。次はこちらです。

$$\begin{align}y&= 2^x\\y&= 3^x\end{align}$$

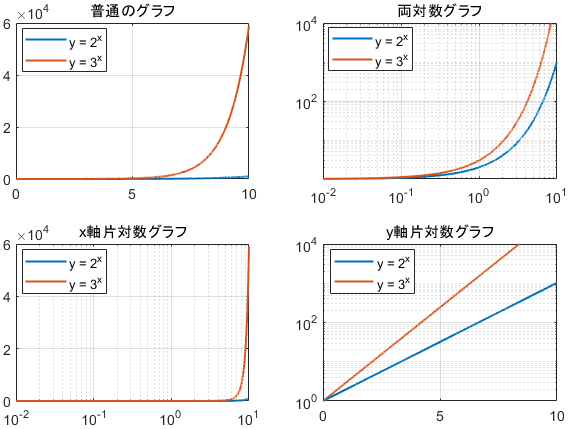
指数関数はy軸片対数グラフが直線になっていますね。指数関数は、次のような「倍々」の特性を持っています。

• $y= 2^x$は、$x$が1増えるごとに$y$が2倍
• $y= 3^x$は、$x$が1増えるごとに$y$が3倍

上記より、y軸でだけ倍々の関係を考えると直線になるわけです。$y= 10^x$ を考えてみるとより分かりやすいですね。

対数関数

最後は対数関数です。

$$\begin{align}y&= \log_{10} x\\y&= 2\log_{10} x\end{align}$$

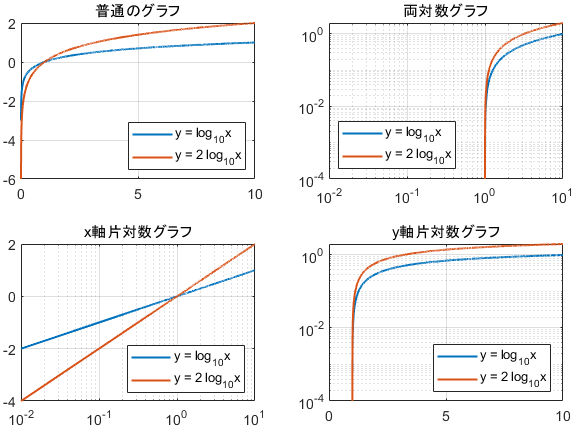
今度はx軸片対数グラフが直線になっています。これは実際にx軸の値を代入してみると明らかですね。10の右肩についている数がそのままy軸の値に使われるので、直線的な関係が成り立ちます。

以上、対数グラフの解説でした。

対数目盛りの読み方と、基本的な関数の対数グラフにおける見え方を知っておけば、対数グラフをほぼ不自由なく使いこなせると思います。チャンスがあればデータ分析にどんどん活用して、分析効率を高めていきましょう！