周波数応答は、インパルス応答・ステップ応答と並び、システムの特性を分析するのに非常に有用なツールですが、初めて学ぶ際はイメージがわきにくいかもしれません。
このページでは、周波数応答・周波数特性・周波数伝達関数の直感的イメージと使い方について解説します。
- sin波状の入力に対するシステムの応答のことを、周波数応答と呼ぶ
- 「様々な周波数(速さ)のsin波に対し、システムがどう反応するか」を周波数特性と呼ぶ
- 伝達関数$G(s)$に$j\omega$を代入した$G(j\omega)$を周波数伝達関数と呼び、周波数特性はこれから計算できる
- 信号を「速さ成分」に切り分けて個別に分析できるのが、周波数解析の強み
システムの周波数応答と周波数特性
安定でプロパーなシステム(※)にsin波を入力すると、定常状態の出力も同じ周波数のsin波になることが知られています。ただし、下図のように振幅と位相は変化する場合がほとんどです。
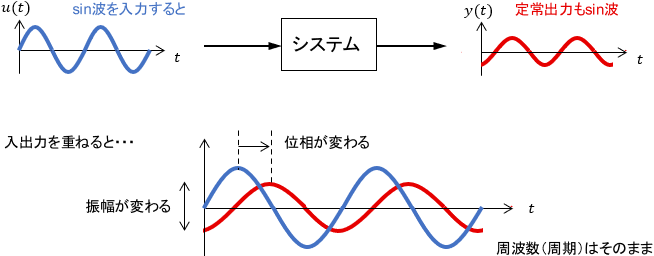

位相の変化は、「信号の出力タイミングの変化」だと思えばOKです。例えば上の図では、位相の変化によってsin波のピークが後ろ方向にずれているので、信号の出力が遅れていることになります。
※「プロパーなシステム」とは、伝達関数が「分子の次数≦分母の次数」を満たすシステムのことです。制御工学で扱う伝達関数のほとんどはプロパーです。詳しくはこちらのページをご覧ください。
上図のような、sin波入力に対する定常応答のことを、周波数応答と呼びます。そして、「様々な周波数のsin波入力に対し、出力の振幅と位相がどのように変化するか」というシステムの特性のことを、周波数特性と呼びます。
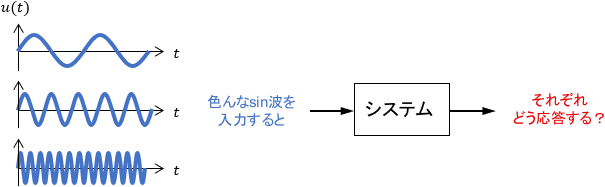

また、周波数の観点でシステムや信号を解析することは、周波数解析と呼ばれます。周波数解析は、現代制御にはない、古典制御ならではの非常に強力な解析手法です。ここからは、そのイメージについて、順番に説明していきましょう。
※現代制御と古典制御の違いについては、こちらのページをご覧ください
周波数応答・周波数特性の直感的イメージ
基本イメージ
まずは、具体例を通じて直感的イメージを深めていきましょう。
例として、ロボットアームの制御を考えます。ロボットアームは関節角度指令値を入力として受け取り、それに応じた関節角度(動作)を出力するとします。
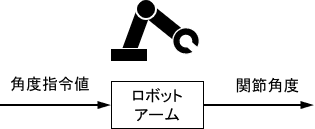

このロボットアームの周波数応答を調べてみましょう。まず、指令値としてゆっくりとしたsin波(周波数の低いsin波)を入れてみます。このときの入出力波形を重ねてプロットすると、次のようになります。
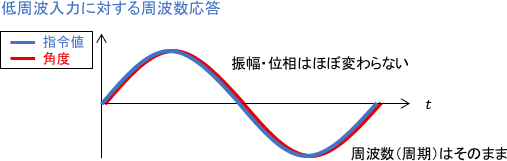

指令値とほぼ同じように、角度もsin波状に変化していますね。
では、だんだん指令値を速くする(周波数を高くする)とどうなるでしょうか?当然どこかのタイミングで、ロボットが指令値の速さについていけなくなりますよね。このときの応答を詳しく見てみましょう。
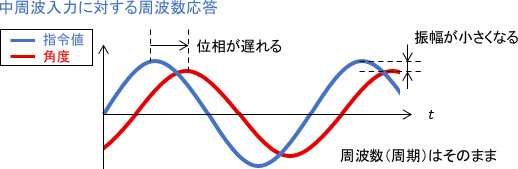

まず、角度が指令値の速さについていけなくなり、位相に遅れが生じていることが見て取れます。さらに、角度が指令値のピークに到達する前に逆方向への指令値が入力されるので、角度の振幅が指令値に対して小さくなっていることも分かります。これが、sin波の位相と振幅が変化するイメージです。一方で、sin波の周波数はそのままとなります。
最後に、指令値を超速くした場合(周波数を超高くした場合)を見てみます。
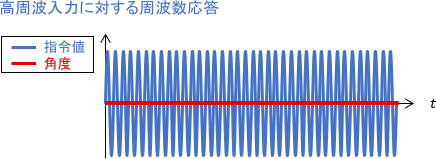

ロボットの反応速度よりも大幅に速い指令値が入っているため、角度の振幅がほぼ0、つまりほぼ動かない状態となっていることが見て取れます。詳しく見ると位相は遅れており、周波数はそのままなのですが、そもそもロボットがほぼ動いていないので、それらの情報はほぼ無意味ですね。
以上より、結局周波数は「信号の変化の速さ」を表しており、周波数特性とは「システムが様々な速さの信号に対してどのように反応するか」を表したものであるとイメージすればOKです。
sin波以外の信号に対するイメージ


ほーん。基本イメージは分かったけど、sin波入力にしか使えないんなら汎用性は低そうだな…
と思うかもしれませんが、そんなことはありません。
フーリエ解析によると、理論上(ほぼ)どんな波形も様々な周波数のsin波に分解できることが知られています。この性質を利用すると、sin波以外の信号に対しても周波数解析を有効に使うことが可能です。
これについて、詳しいイメージを説明していきましょう。
sin波を足し合わせてシステムに入力するとどうなる?
まず伝達関数のおさらいですが、伝達関数で表されたシステムに「異なる2つの信号の和」を入力したとき、その出力は「それぞれの信号単体に対する出力の和」となります。
$$\begin{gather}入力\ U(s) = U_1(s) + U_2(s) \quad のとき、\\[10pt] 出力\ Y(s) = G(s) U(s) =\ubgd{G(s) U_1(s)}{U_1(s)に}{対する出力} + \ubgd{G(s) U_2(s)}{U_2(s)に}{対する出力}\end{gather}$$


よって、複数のsin波の和をシステムに入力すると、その出力はそれぞれのsin波に対する周波数応答の和となります。
例えば先ほどのロボットアームの例にて、低周波入力と高周波入力を足し合わせた入力をロボットに与えた場合、ちょうど信号の高周波成分(速い信号成分)だけが消えたような出力が得られることになります。
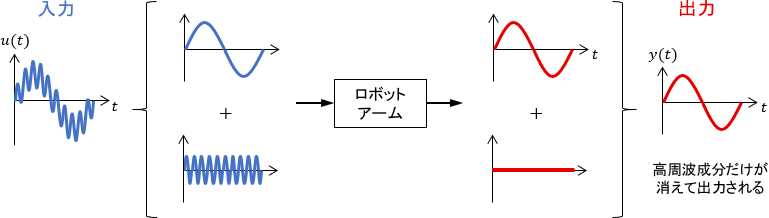

つまりこのロボットは、信号の高周波成分をカットするような性質を持っているということですね。
このように信号を一度sin波に分解して考えることで、信号の周波数(速さ成分)に基づいた観点でシステムの性質を評価できるのが周波数解析の強みだと言えるでしょう。
どんな信号もsin波に分解すれば周波数解析ができる
この考え方を応用すると、どんな入力信号でもそれを様々な周波数のsin波に分解し、それぞれに対する出力の様子を見れば、システムの性質を周波数に基づいて評価できることになります。
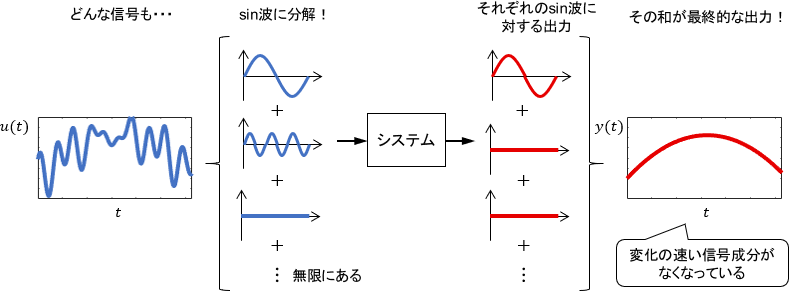

ただ、任意の信号をsin波に分解するには、理論上無限個の周波数のsin波を用意する必要が生じます。よって周波数解析では、無限個の周波数を分かりやすく扱うために下図のように横軸を周波数・縦軸をsin波の振幅(&位相)としたグラフが用いられることがほとんどです。(このグラフを書くのに使われるのがフーリエ変換です)
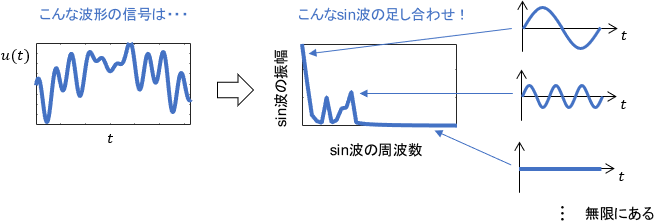

※上図の「sin波の振幅」のグラフと同様に、縦軸が「sin波の位相」となったグラフもセットで用いられますが、スペースの都合から省略しています。以降の図でも同じです。
この表現を用いて先ほどの入出力関係を見ると、下図のようにシステムによって周波数の「成分」に変化が生じていると解釈できます。
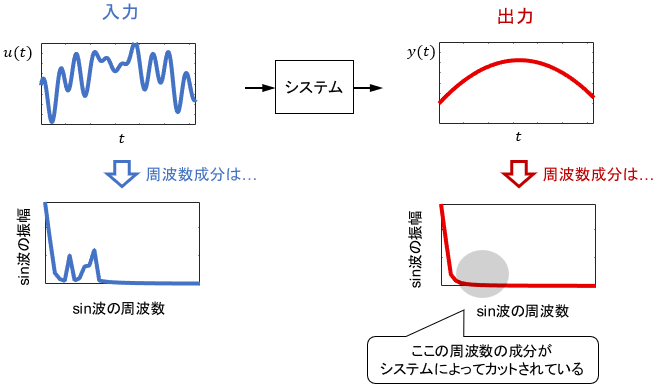

結局、入力信号の「速さ成分」がそれぞれどのように変化するかを見ていることになりますね。このように、ゴチャゴチャしていた信号も「速さ成分」に切り分けて個別に分析できるのが、周波数解析の強みです。
周波数特性の求め方


ほーん。便利なのは分かったけど、結局システムの周波数特性はどうやったら分かるの?色んなsin波を入れまくるの?めんどくさそう…
と思うかもしれません。確かに全周波数のsin波をシステムに入力し、周波数応答を全て確認するのは現実的に不可能です。ただし、そんなことしなくてもシステムの周波数特性がちゃんと分かるのが周波数解析のすごいところです。
ここからは、そんな周波数特性の求め方について説明していきます。
インパルス応答と周波数特性
アイデアとしては簡単で、sin波を1つずつ入力するのではなく「全周波数のsin波の和」を1つの信号としてシステムに入力することを考えます。
当然、この入力に対する出力は「全周波数のsin波それぞれに対する出力の和」なので、その周波数成分がそのままシステムの周波数特性を表していることになります。
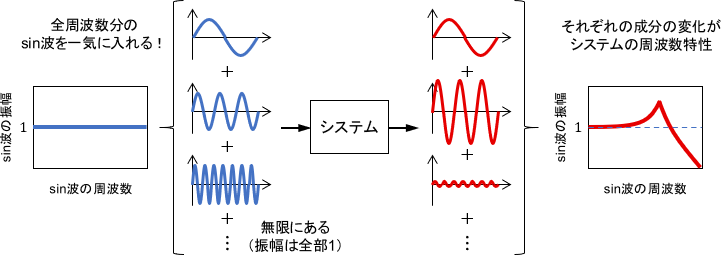

そして、この「全周波数のsin波の和」はインパルス関数になることが知られています。
ということは、インパルス関数に対する出力(つまりインパルス応答)をフーリエ変換したものが、そのままシステムの周波数特性を表していることになります。
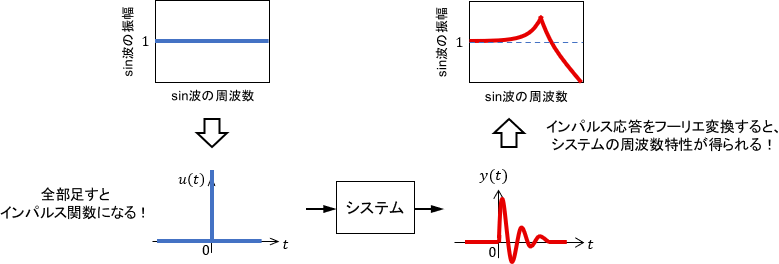

※インパルス関数やインパルス応答の詳細については、こちらのページをご覧ください。
周波数伝達関数による解析的な求め方


ほーん、インパルス応答のフーリエ変換ね…
やっぱめんどくさそう…
大丈夫です!インパルス応答のフーリエ変換は比較的お手軽に計算できます。これについて、順番に説明していきましょう。
まず、システムのインパルス応答$Y(s)$を計算しましょう。伝達関数$G(s)$で表されるシステムにインパルス入力$U(s)=1$を与えればOKですね。
$$Y(s) = G(s) U(s) = G(s)$$
当然、伝達関数そのものが出てきます。インパルス応答からシステムの特性が分かるのにも納得がいきますね。
で、このインパルス応答$G(s)$のフーリエ変換ですが、$s$に$j \omega$を代入した$G(j \omega)$により計算できることが知られています($\omega$はsin波の角周波数、$j$は虚数単位です)。
この、システムの周波数特性を表す式$G(j\omega)$は周波数伝達関数と呼ばれ、周波数解析において非常に重要な役割を持ちます。
※厳密に言うと、特定の条件にて$G(j \omega)$はインパルス応答のフーリエ変換と完全に一致しなくなりますが、実用上は同一視してほとんど問題ありません。
※角周波数$\omega$が出てきましたが、これも結局は振動の周波数を表すものです(単位が違うだけ)。よって、以降も「sin波の周波数」のつもりで読めばOKです。詳細は、こちらのページをご覧ください。
例として、次の伝達関数$G(s)$で表される1次系の周波数特性を求めてみましょう。
$$G(s) = \frac{K}{Ts+1}$$
周波数伝達関数$G(j\omega)$を求め、式を整理します。
$$\begin{align}G(j\omega) &= \frac{K}{T\omega j+1} = \frac{K(T\omega j-1)}{(T\omega j +1)(T\omega j -1)}\\[10pt] &= \ubg{\frac{K}{T^2 \omega ^2 + 1}}{実部=aとする} + \Bigl( \ubg{ – \frac{KT \omega}{T^2 \omega ^2 + 1}}{虚部=bとする} \Bigr) j\\[10pt] &= a+bj \end{align}$$
伝達関数に虚数を代入しているので、計算結果は複素数となりますね。これを複素平面上にプロットしたとき、複素平面上のベクトル$G(j\omega)$と周波数特性は、次の関係性を持ちます。
- ベクトルの絶対値$|G(j\omega)|$:sin波の振幅が何倍になるか。ゲインと呼ばれる
- ベクトルの偏角 $\angle G(j\omega)$:sin波の位相が何度ずれるか。位相(または位相差)と呼ばれる
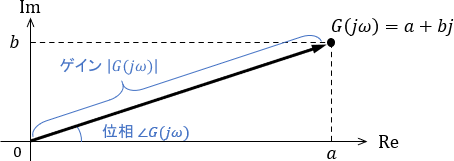

上図を元に、ゲイン$|G(j\omega)|$と位相$\angle G(j\omega)$は次のように計算できます。
$$\begin{align}|G(j\omega)|&= \sqrt{a^2+b^2} \\[5pt] \angle G(j\omega) &= \tan ^{-1}\left( \frac{b}{a}\right)\end{align}$$
実部$a$と虚部$b$は入力信号の角周波数$\omega$によって値が変わるため、上式に特性を知りたい角周波数を代入すれば、それに対する周波数特性が分かります。また、上式を$\omega$の関数としてプロットすれば、様々な各周波数に対する周波数特性が一気に分かるというわけですね。


様々な角周波数に対する周波数特性を表す方法としては、ボード線図やベクトル軌跡がよく用いられます。
※ボード線図とベクトル軌跡については、こちらのページで詳しく解説していますので、合わせてご覧ください。
実験的な求め方
ここまで、伝達関数の式から解析的に周波数特性を求める方法について解説してきました。
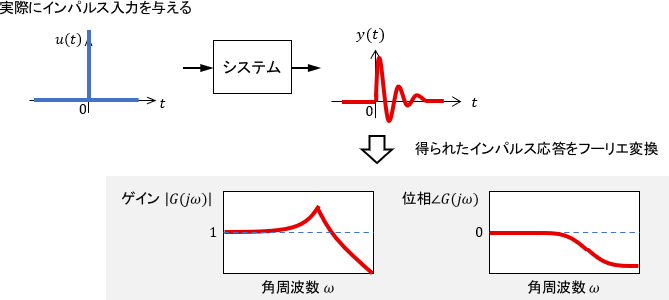
一方で、インパルス応答は実際にシステムを動かして得ることも可能です。よって、インパルス応答のデータをフーリエ変換することによって、実験的にシステムの周波数特性を求めることも可能です。

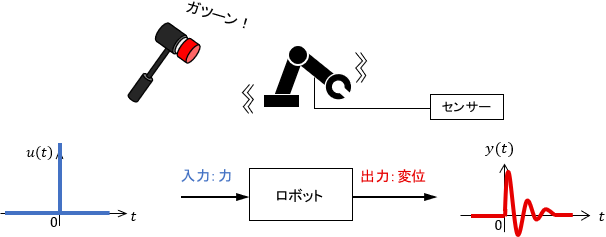
具体例としては、機械システムの周波数特性(振動特性)を確認するインパルス加振実験が代表的です。ハンマーで対象をぶっ叩いて、インパルス応答を分析するわけですね。

ただし、理想的なインパルス信号を現実に与えることは困難であることや、フーリエ変換の窓関数の影響により、この方法で得られる周波数特性には必ず誤差が含まれます。とはいえ、実用上は非常に有用な方法です。
以上、周波数応答・周波数特性・周波数伝達関数の直感的イメージと使い方でした。
- sin波状の入力に対するシステムの応答のことを、周波数応答と呼ぶ
- 「様々な周波数(速さ)のsin波に対し、システムがどう反応するか」を周波数特性と呼ぶ
- 伝達関数$G(s)$に$j\omega$を代入した$G(j\omega)$を周波数伝達関数と呼び、周波数特性はこれから計算できる
- 信号を「速さ成分」に切り分けて個別に分析できるのが、周波数解析の強み









コメント