制御工学は、大きく古典制御と現代制御という分野に分けられます。このページでは、それぞれの違いと利点について説明します。
| 古典制御 | 現代制御 | |
|---|---|---|
| 主な計算手段 | 手計算 | コンピュータ計算 |
| 扱える入出力数 | 1入力1出力のみ | いくつでもOK |
| 扱えるシステム | 線形時不変システムのみ | だいたい何でもOK |
| 扱う変数領域 | $s$領域(周波数領域) | $t$領域(時間領域) |
| システムの表現 | 伝達関数 | 状態方程式 |
- 基本的に現代制御のほうができることが多くて高性能
- ただし、古典制御には周波数解析や安定余裕解析といった独自の強みがある
名前の由来
古典・現代という名前は、歴史に由来します。
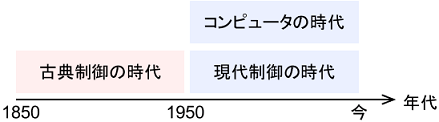
古典制御は1850年ごろから盛んに研究され、1950年ごろにだいたい今の形になったとされています。一方、現代制御は1950年ごろから盛んに研究され、今も進化を続けています。
この歴史に基づき、古典制御は「昔の制御」なので「古典」、現代制御は「最近の制御」なので「現代」という名前がついています。
両者を考える上で重要なのは、コンピュータの存在を前提としているかどうかです。古典制御は手計算を前提とした制御、現代制御はコンピュータ計算を前提とした制御、とイメージするとよいでしょう。
※それぞれの歴史(物語)はこちらのページで詳しく紹介していますので、興味がある方はご覧ください
取り扱えるシステムの違い
入出力数の違い
古典制御
古典制御で取り扱えるのは、単入力単出力システムのみです。
単入力単出力システムとは、その名の通り入力と出力が1つずつであるシステムのことで、SISOシステム(Single-Input Single-Outputシステム)とも呼ばれます。

現代制御
一方、現代制御では入出力の数に制限がなく、多入力多出力システムを扱えます。多入力多出力システムはMIMOシステム(Multiple-Input Multiple-Outputシステム)とも呼ばれます。

もし古典制御で本質的に多入力多出力なシステムを扱う場合は、扱う信号を絞って単入力単出力システムとみなす必要があります(先ほどの図の通り)。対して現代制御ではそのような制約がないため、対象システムをそのまま取り扱うことが可能です。
数式モデルの構造の違い
古典制御
古典制御で取り扱えるのは、数式モデルが「線形」で「時不変」なシステムのみです(ちょっぴり例外はありますが)。このようなシステムは、まとめて「線形時不変システム」と呼ばれます。
超簡単に説明すると、線形時不変システムとは、数式モデルが次式のように「定数×入出力(の微分)」の項だけで表されるシステムのことを指します。
$$a_2 \ddot{y} + a_1 \dot y + a_0 y = b_1 \dot u + b_0 u$$
現代制御
一方で現代制御は、線形・非線形・時変・時不変問わず様々なシステムを扱えます。「だいたいどんなシステムでも扱える」と考えて構いません。
もちろんシステムが複雑化するほど取り扱いも難しくなりますが、コンピュータ計算によってそれをカバーするのが基本方針です。
※線形・非線形・時変・時不変の違いについては、こちらのページをご覧ください。
システムの表現の違い
基本となる変数の違い
現代制御
まず現代制御を先に説明したほうが分かりやすいと思うので、現代制御から見ていきましょう。
現代制御では、数式モデルを時間$t$に基づいて処理します。この時間$t$に基づいた世界は、$t$領域(または時間領域)と呼ばれます。時間に基づくので、人間の直感と合致した扱い方であると言えるでしょう。
しかし、数式モデルはほとんどが微分方程式で表されるため、それをそのまま解くのは結構大変です。

古典制御
そこで古典制御では、ラプラス変換という変数変換を用いて、時間$t$を$s$という変数に変換します。そして、この$s$に基づいて数式モデルを処理します。
この$s$に基づいた世界は、$s$領域(または周波数領域)と呼ばれます。$s$領域では、微分方程式を手計算で解くのがとても簡単になることが知られています。

下図のように「とりあえず問題を$s$領域に変換し、計算が簡単な世界で処理したあと、得られた答えを$t$領域に戻す」というのが基本的なイメージです。
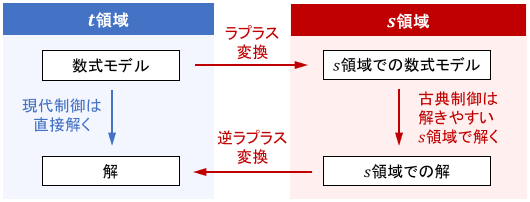
※ラプラス変換の詳細については、こちらのページをご覧ください
数式モデル表現の違い
基本となる変数が違うため、古典制御と現代制御では、当然数式モデルの表現も異なります。
ここからは、次の機械システムのモデリングを題材に、それぞれの具体的な違いを見ていきましょう。
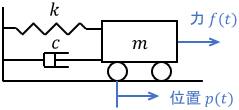
$p(t)$は台車の位置、$f(t)$は台車に加わる力、$m$は台車の質量、$k$はばね定数、$c$は粘性抵抗係数です。このシステムの性質は、次の通り運動方程式で表されますね。
$$m\ddot{p} + c \dot{p} + kp = f$$
古典制御
古典制御では$s$領域にて処理を行うため、数式モデルも$s$に基づいた式で表します。これを伝達関数と呼びます。
$$こういうやつが伝達関数: G(s) = \frac{b_1 s + b_0}{s^2 + a_1 s + a_0}$$
$a_*, b_*$は定数です。先ほどの機械システムを伝達関数で表すと、次のようになります。

上図のように、伝達関数は$t$領域で表された数式モデルを丸々ラプラス変換したものです。ブロック線図では、次のように表されます。
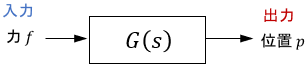
※伝達関数の詳細については、こちらのページをご覧ください。
現代制御
一方で現代制御では、ベクトルや行列を用いて、時間$t$に関する1階の連立微分方程式の形でシステムを表現します。この式を状態方程式と呼びます。
$$こういうやつが状態方程式: \dot{x} = Ax + Bu $$
$x$は状態ベクトル、$u$は入力ベクトル、$A,B$は行列です。先ほどの機械システムを状態方程式で表すと、次のようになります。
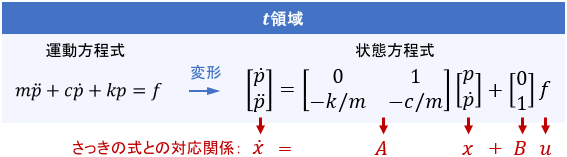
伝達関数は入力と出力の関係のみを考慮していましたが、状態方程式では数式モデルを構成する変数全てを、システムの「状態」として考慮に入れるのが特徴です。
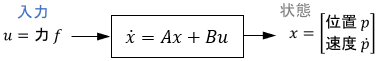
上の例だと、台車の位置$p$だけでなく速度$\dot{p}$も状態$x$の中で考慮されていますね。これはシンプルな例ですが、システムが複雑になるほど考慮される状態も増えていきます。
ただ、これだけでは状態$x$のうち、どの情報がシステムの出力として外に取り出せるのかが分かりません。そこで、出力方程式によって状態と出力の関係性を表します。
$$こういうやつが出力方程式: y = Cx $$
$y$は出力ベクトル、$C$は行列です。例えば先ほどの機械システムの例にて、台車の位置$p$のみがセンサーで読み取れる(出力として取り出せる)とすると、出力方程式は次のように表されます。

このように、出力方程式は「現実的に(センサーなどで)どの状態を取得できるか」を表すことがほとんどです。
以上をまとめると、現代制御におけるシステムは、状態方程式と出力方程式を組み合わせた次のブロック線図で表されます。
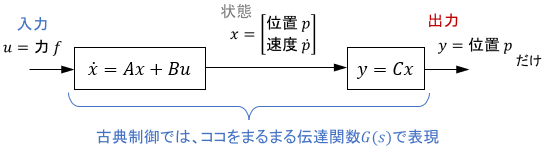
このようなシステムの表現方法は、状態空間表現とも呼ばれます。
古典制御では伝達関数によって入力と出力の関係だけをざっくり表していたのに対し、現代制御では状態方程式によってシステムの内部までもれなく考慮に入れていると言えます。
強み・利点の違い
現代制御の強み・利点
以上のとおり、現代制御は適用対象が広く、システムの内部をすべて考慮に入れるため、基本的に古典制御よりできることが多く、高性能を出しやすいです。
特に、制御目的に対して最適な制御入力を逆算する最適制御は、現代制御を代表する非常に強力な制御手法です。システムの内部をすべて考慮に入れるからこそ、最適な制御入力を求められると言えます。
古典制御の強み・利点
一方で、古典制御は適用対象が限られており、システムの入出力関係しか考慮しないため、現代制御ほどの高性能は出せないことがほとんどです。
しかし、古典制御は周波数解析や安定余裕解析など、現代制御にはない独自の強みを持っています。それぞれ簡単に紹介していきましょう。
周波数解析
周波数解析は、「システムが様々な周波数の信号成分に対してどのように反応するか」を解析する手法です。(周波数は「信号の変化の速さ」だと思ってください)
これにより、考慮しているシステムに対して「この周波数の信号成分に特に過敏に反応する」とか「これ以上の周波数にはあまり反応しなくなる」といった情報を知ることができます。
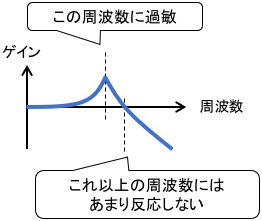
ラプラス変換は周波数解析との相性が非常に良いため、周波数解析は古典制御の得意分野となっています。
※周波数解析についてはこちらのページで解説していますので、合わせてご覧ください。
安定余裕解析
一方の安定余裕解析は、システムが安定だとしたときに、それが余裕で安定なのか、ギリギリ安定なのか、といった安定性の度合いを解析する手法です。
実際に使うシステムがギリギリ安定では困るので、実用上非常に有用な解析手法であると言えます。
※安定余裕解析の詳細については、こちらのページをご覧ください
適用対象の違い
現代制御がよく使われる対象
現代制御は、数式モデルを精度良く導出できるシステムによく使われます。
例えば機械システムでは、ロボット・車・ドローンなど、その特性を運動方程式で表現できるものによく適用されます。電気システムでは、レギュレータ回路・モーター回路など、その特性を微分方程式で表現できるものによく適用されます。
特に、「動作の誤差を極力小さくしたい」「エネルギー効率を最大化したい」といった高度な制御目的に対してよく利用されます。
古典制御がよく使われる対象
古典制御は、周波数特性が特に重要となるシステムによく使われます。
例えば機械システムでは、振動抑制制御によく用いられます。振動の周波数が非常に重要となりますからね。電気システムでは、特定の周波数入力をカットするフィルタ回路を設計する場合などに用いられます。周波数情報が重要となる信号処理分野でも、古典制御の知見が頻繁に活用されます。

また、「システムの厳密な数式モデルは分からないけど、そこそこの性能でいいから手軽に動かしたい!」という場合も古典制御がよく用いられます。古典制御が生まれた時代の制御目的はまさにコレですからね。

例えばPID制御は、システムのモデルが全く分からなくてもパラメータチューニング(試行錯誤的な調整)によってそこそこの性能を出しやすい制御手法です。「この世で使われている制御器の8割はPID」と言われるほど、非常に広く用いられている実用的な手法です。
※PID制御の概要については、こちらのページをご覧ください
以上、古典制御と現代制御の違いと利点についての説明でした。どちらも一長一短の特徴があるので、問題によって適切に使い分けていきましょう。
| 古典制御 | 現代制御 | |
|---|---|---|
| 主な計算手段 | 手計算 | コンピュータ計算 |
| 扱える入出力数 | 1入力1出力のみ | いくつでもOK |
| 扱えるシステム | 線形時不変システムのみ | だいたい何でもOK |
| 扱う変数領域 | $s$領域(周波数領域) | $t$領域(時間領域) |
| システムの表現 | 伝達関数 | 状態方程式 |
- 基本的に現代制御のほうができることが多くて高性能
- ただし、古典制御には周波数解析や安定余裕解析といった独自の強みがある











コメント