このページでは、初学者向けに制御工学の概要を分かりやすく解説します。特に、制御工学の楽しさ・強み・難しさについて詳しく説明します。
- 制御工学は「この世界を意のままに操る学問」
- 制御工学は楽しい!自分がちょっとした神様になれるのが醍醐味
- 適用範囲が超広く、様々な分野で必要とされるのが強み
- 制御工学の難しさは「誤差」「制約」「理論」
制御工学とは
制御工学を一言で表すと、「この世界を意のままに操るための学問」です。
順に説明していきましょう。この世の現象は、物理学の様々な分野にてその法則が解明され、方程式(数式モデル)としてまとめられています。次のものが代表的ですね。
- 機械力学の運動方程式
- 流体力学のナビエ・ストークス方程式
- 電磁気学のマクスウェル方程式
これらの方程式のおかげで、我々は実際に経験することなく将来を予測できるわけです。この点で、物理学は「この世界の仕組みを解明し、将来を予測する学問」であると言えます。
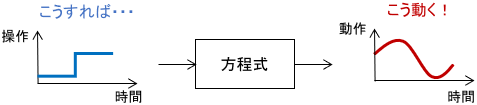
経験せずに将来が予測できるというのは、大変便利です。ただ、せっかく将来を予測できるなら、その将来を自分の思い通りにしたいと思うのが人間ですよね。その方法を学問として追及するのが制御工学です。
制御工学の楽しさ
制御工学は、使いこなせればとても楽しい学問です。
上述のように、物理工学全般は「対象の分析」が主になりがちな学問ですが、制御工学は珍しく「対象を操る」ことに重きをおいた学問だと言えます。
もちろん分析も面白いですが、分析から一歩進んで「操る」フェーズに移ると「工学してる感」が増し、一気に楽しくなってきます。
想像してみてください。あなたは制御工学の知識を駆使して、何かを思い通りに操っています。仕事で使う大きな装置でも、おもちゃのラジコンでもOKです。

対象が何であれ、「思い通りに操る」というのは楽しいものですよね!
この楽しさの根源は、自分がちょっとした神様になったような感動です。あなた自身が、その空間をすべて支配しているわけです!
結局、工学の醍醐味ってこういう所ですよね。
最初はシンプルなものしか扱えないかもしれませんが、制御工学を学べば学ぶほど、ロボット・車・ドローンなど、なんでも意のままに操ることが出来るようになります。想像するだけでワクワクしますね!
制御工学の強み
ここからは、学問としての制御工学の強みについて解説していきます。
適用範囲が超広い!
制御工学は、適用範囲がとても広いのが大きな特徴です。これについて、詳しく見ていきましょう。
制御工学では、「制御対象の特性を数式モデルで表し、それに基づいて制御方法を設計する」というアプローチを取るのが基本です。

※このような制御開発のアプローチ(手順)については、こちらのページをご覧ください
ここで注目したいのは、機械・電気・流体・材料・経済など世の中に様々にある制御対象を、「数式モデル」という抽象化した1つの概念で取り扱う点です。
これによって、どんな制御対象でも一度数式モデルに落とし込みさえすれば、その後は制御理論を等しく適用できることになります。
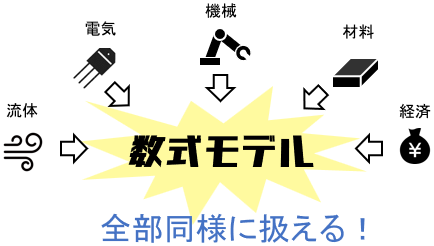
つまり、一度制御工学を理解すれば、それだけで様々な制御対象を扱えるわけですね!
この守備範囲の広さが、制御工学の最大の強みであると言えるでしょう。
めちゃくちゃツブシがきく!
上述の通り制御工学は適用範囲が超広いため、様々な分野の応用フェーズにて必要とされます。
工学の各分野には、「材料屋さん」「流体屋さん」「電気屋さん」といった専門家が存在しますよね。この人たちはそれぞれの対象のスペシャリストではありますが、「操るスペシャリスト」ではありません。
よって対象をバリバリ動かす応用フェーズになると、「操るスペシャリスト」として制御屋さんが必要となることが多々あります。

言い換えると、制御工学はめちゃくちゃツブシがきく技術であると言えるでしょう。
技術をしっかり持った制御屋さんは食いっぱぐれません。一度習得すると、だいたいどんな業種でも必要とされるわけですからね。

また、裏を返すと、制御屋さんは「様々な分野で様々な対象に触れられる立場にある」とも言えます。「制御工学という1つの技術を切り口に、ロボット・車・電気回路など様々な対象で遊べる」と考えると、かなりコスパの良い技術に聞こえますよね!
制御以外もわりと分かるようになる!
前述の通り、制御工学では対象を数式モデルで抽象化して扱います。実は、この抽象化した世界での「制御工学的な考え方」を持っていれば、他分野の理論もわりとすんなり理解できてしまったりします。
例えば古典制御には周波数解析と呼ばれる、「数式化された対象を周波数の観点で分析する手法」があります。
この理論と考え方を理解していると、同じく周波数がカギとなる振動工学や信号処理の理論もわりとすんなり理解できるようになります。
※周波数解析の詳細については、こちらのページをご覧ください
また、現代制御には最適制御と呼ばれる、「目的を数式化し、それに基づいて最適解を求める手法」があります。この考え方、制御に限らず様々な分野で活用できそうですよね。
実際その通りで、例えば最近目覚ましい発展を遂げているAI・機械学習の分野では、この考え方が基盤となっている手法が多々あります。
つまり、最適制御の理論と考え方を理解していると、上記分野もかなりすんなりと理解できてしまうわけです。

こう聞くと、制御工学ってとてもオトクな学問に聞こえますね!
そもそも「制御工学」という学問自体が、機械や電気など様々な分野の技術を抽象化し、体系的に統合して生みだされたものです。よって、このコスパの高さはある意味必然であるとも言えるでしょう。
※そんな制御工学の生い立ちについては、こちらのページをご覧ください。(面白いよ!)
制御工学の難しさ
…と、制御工学の良い面ばかり紹介してきましたが、当然「この世界を意のままに操る」というのは、そう簡単なことではありません。

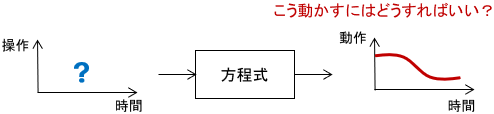
制御対象の数式モデルがあるなら、それを逆算すればいいだけじゃないの?
と思われるかもしれません。基本的な考え方はその通りなのですが、実際やってみると意外と一筋縄ではいかないことが分かります。
ここからは、そんな制御工学の難しさについても簡単に説明していきましょう。
基本的に、制御工学は「誤差」「制約」「理論」の3つと戦う学問です。以下、それぞれの詳細を説明していきます。
誤差
物理の方程式には必ず誤差があります。例えばラジコンを制御するために、ラジコンの数式モデルを作成したとします。その際、次のような誤差がほぼ必ず含まれます。
- パラメータの誤差(例:質量や摩擦係数の誤差など)
- 数式モデルそのものの誤差(例:空気抵抗が式中で考慮されていないなど)
そしてこれらの影響で、方程式の計算結果にも誤差が生じてしまいます。よって、単純に「数式モデルから自分の望む結果を逆算する」というだけでは、望む結果が得られないことがほとんどです。
制御工学ではフィードバック制御と呼ばれる手法により、これを解決することがほとんどです。フィードバック制御は、一言でいうと「実際の状況を観測し、それに応じて制御を微調整する手法」です。
※フィードバック制御の詳細については、こちらをご覧ください
制約
たとえ数式モデルに誤差が全く無いとしても、制御には制約という難しさがあります。
再びラジコンの制御を想像してみましょう。次の通り、ラジコンの性能には様々な限界がありますよね。
- 方向転換できる角度(ハンドリング性能)
- 走れる速さ(モーター性能)
- 連続走行できる時間(バッテリー性能)
当然、制御もこれらの限界の範囲内で実現する必要があります。これが制約です。
制約の中でいかに対象を操るか、これを考えるのも制御工学の仕事というわけですね。
制御工学において制約を扱う方法は様々にあり、ケースバイケースで方法を選んで対応する、というのが現実です。
理論
誤差・制約の2つは制御工学が戦ってくれますが、理論だけは我々が直接戦うしかありません(涙)
制御工学は理論が複雑になりがちです。 高度な制御理論のほとんどは、大学レベルの物理・数学の知識を前提としているため、制御工学のテキストを開いて「あ、無理」と諦めた方も多いのではないでしょうか。
ただ、安心してください。確かに高度な制御手法は理論が複雑ですが、シンプルで実用的な制御手法も数多く存在します(そして前述の楽しさを味わうことができます!)
本サイトでは、皆さんが苦しまずにステップアップできるよう、様々な制御理論を直感的に解説していますので、是非参考にしてくださいね!
※こちらのページでは、制御の世界の全体像を解説していますので、合わせてご覧ください。
- 制御工学は「この世界を意のままに操る学問」
- 制御工学は楽しい!自分がちょっとした神様になれるのが醍醐味
- 適用範囲が超広く、様々な分野で必要とされるのが強み
- 制御工学の難しさは「誤差」「制約」「理論」









コメント