このページでは、下記ページで紹介した「制御の全体像」の中の、古典制御と現代制御の中身をクローズアップして紹介します。
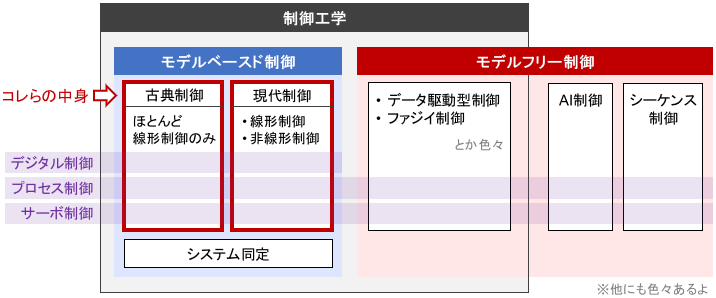
上記ページで紹介したのは制御の「大ジャンル」にあたるものでしたが、本ページで紹介する各種手法は制御の「中ジャンル」にあたるものです。つまり、それぞれの中にも様々な手法や流派がありますので、それを念頭に読んでくださいね!
※古典制御と現代制御の違いについては、こちらのページをご覧ください
古典制御
PID制御
PID制御は、比例要素・積分要素・微分要素の組み合わせで構成される、最も基本的でシンプルな制御手法です。
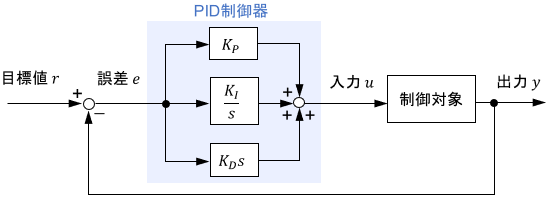
$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{比例\ P} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{積分\ I} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{微分\ D}$$
それぞれの制御要素のゲイン($K_P$など)をチューニングすることで、制御性能を調整します。調整は数式モデルを用いて理論的に行う事もできますが、実際に制御対象を動かしながら試行錯誤的にやることが多いです(そのほうが簡単なので)。
最大の利点はその使いやすさで、制御工学をよく知らない人でもお手軽に80点くらいの性能を出せてしまうことが多いです。原始的ながらも「この世で使われている制御器の8割はPID」と言われるほど、非常に広く使用されている制御器です。
通常のPID制御に加え、微分先行型PID制御・I-PD制御など、様々な特徴を持った派生版が存在します。
※PID制御の詳細については、こちらのページをご覧ください
ループ整形法
制御システム全体の周波数特性が意図通りになるように、制御器を設計する手法です。制御器を1つのシステムとみなし、そのシステムがどのような特性を持つべきかを考え、設計します。
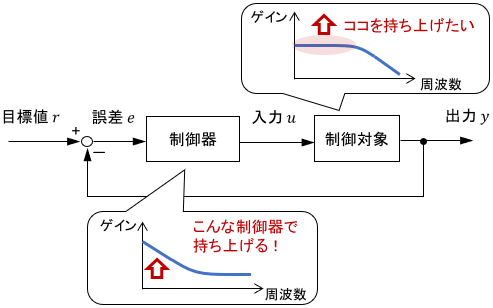
PID系よりも複雑な制御器を、理論に基づいて取り扱えるのが利点です。
※システムの周波数特性については、こちらのページをご覧ください
根軌跡法
あるパラメータ(通常は制御ゲイン)を0からだんだん大きくしていったとき、システムの極がどのように変化していくのかを図で表したものを根軌跡(Root Locus)と呼びます。この根軌跡に基づいて、適切な制御ゲインを設計する手法が根軌跡法です。
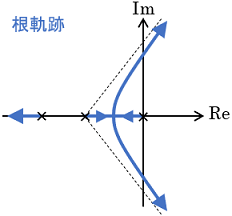
極は「わざわざ方程式を解かなくてもシステムの挙動がある程度分かる、便利なパラメータ」だと思ってください。
根軌跡上での極の動きにはある程度法則性があるため、実際に極を隅々まで計算することなく、ある程度お手軽に根軌跡を描けるのが特徴です。
根軌跡法の利点としては、設定パラメータと、それが生み出す動作を視覚的に対応付けられることが挙げられます。生まれた当時は画期的でよく使われたようですが、コンピュータを用いた制御器設計が発達した現在では、あまり使われることはありません。
※システムの極については、こちらのページをご覧ください
2自由度制御
2自由度制御は、フィードバック制御とフィードフォワード制御を組み合わせた制御です。
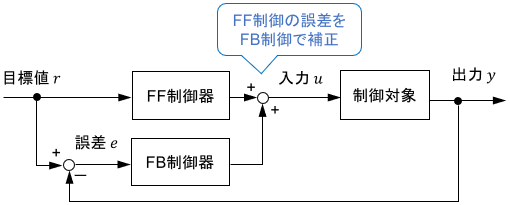
通常のフィードバック制御は誤差$e$のみに基づいた制御、フィードフォワード制御は目標値$r$のみに基づいた制御ですが、それらを組み合わせることで$e$と$r$(または$y$と$r$)2つの情報に基づいた制御が可能となるため、2自由度制御と呼ばれます。
2自由度制御の利点としては、フィードバック制御の高い追従精度と、フィードフォワード制御の速い反応速度を両立できることが挙げられます。
※フィードバック制御・フィードフォワード制御の特性については、こちらのページをご覧ください
現代制御
最適制御
最適制御(Optimal Control)は、制御対象と制御目的を数式で表し、それらに基づいて最適な制御入力を求める手法です。
制御目的は「次式で表される評価関数$J$をなるべく小さくしたい」という形式で表現され、これを最小化する入力を導出することで最適制御が実現されます。
$$J= \ubg{\phi \bigl( x(t_f) \bigr)}{終端コスト} + \ubg{\int ^{t_f} _{t_0} L\bigl(x(t), u(t)\bigr)dt}{ランニングコスト} $$
終端コストは「最終状態がどのようになってほしいか」を、ランニングコストは「最終状態までどのように行ってほしいか」を反映させるものです。関数$\phi$や$L$には、「最小化したいもの」を設定します。「制御量と目標値との誤差」や「投入される制御入力量」などがよく設定されます。
こういった枠組みの中で、自分の制御目的をいかに評価関数に落とし込むかが、設計者の腕の見せどころとなります。
最適制御の最大の利点は、評価関数に対し「これ以上いい方法は絶対にない」という文字通り最適な制御が可能となることです。状態方程式でシステムの特性をすべて考慮に入れる現代制御ならではの、非常に強力な制御手法であるといえます。
メジャーな線形最適制御の種類としては、次のものがあります。
- LQR制御:状態を0に持っていくことを目指す、最も基本的な最適制御
- LQI制御:状態を任意の一定値に持っていくことを目指す最適制御
- LQG制御:制御対象に含まれるノイズも考慮した最適制御。平たく言うと、LQRとカルマンフィルタの組み合わせ。
バンバン制御
バンバン制御(Bang–Bang Control)はON-OFF制御とも呼ばれ、制御入力が2つの値のどちらかしか取らない制御を意味します。
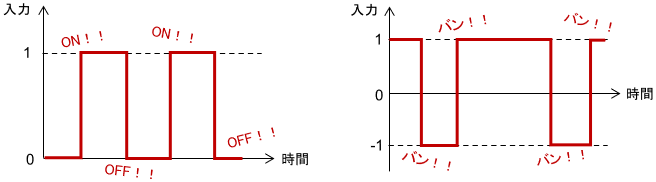
システムをスイッチのON・OFFでしか制御できない場合は、必然的にコレになります。例えば安物のコタツは、「温度が設定値より低ければヒーターON、高ければヒーターOFF」といった動作で温度制御されますが、これはバンバン制御です。
最大の利点は、安くて単純な構成で実現できる点です。一方、制御入力が急激に変化するため、制御対象の挙動が滑らかになりにくいことが欠点です。
また、普通の最適制御が結果的にバンバン制御になる場合もあります。その典型的な例が、最短時間制御です。例として、車を現在地から目的地へ移動させる制御を考えましょう。

制御入力はアクセル・ブレーキ操作、つまり車の加速度です。このとき、「目的地へ到達するまでの時間」を最小化する最適制御入力は、結果的にバンバン制御となります。
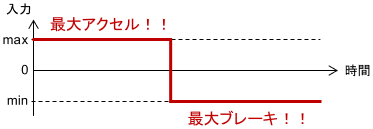
最初にアクセルを思いっきり踏み、「今だ!」というタイミングでブレーキを思いっきり踏むのがベストということですね。直感的にも納得がいくと思います。
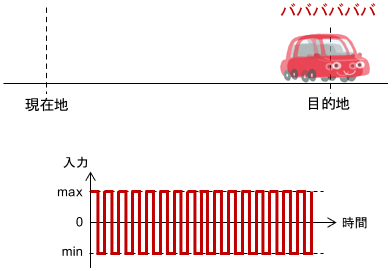
ただし、現実には目的地に寸分違わず止まることはできず、目的地付近でガクガクとチャタリングが発生してしまいがちなので、何かしらの対策が必要となります。
適応制御
適応制御(Adaptive Control)は、直近の動作実績に応じて、制御器や数式モデルのパラメータを自動で調整しながら制御する手法です。
最適制御は非常に強力ですが、数式モデルに誤差があると当然その性能も低下します。とはいえ現実のシステムは、経年劣化や動作条件によってその特性が変動するので、数式モデルには必ず誤差が含まれます。適応制御の利点は、各種パラメータを自動で調整することで、この誤差を低減できることです。
適応制御は、モデル規範型適応制御(MRAC)とセルフチューニングレギュレータの2種類に大別されます。
モデル規範型適応制御は、数式モデルの誤差をカバーするように制御パラメータを補正する方法です。直接法とも呼ばれます。適応制御界ではこちらが主流です。
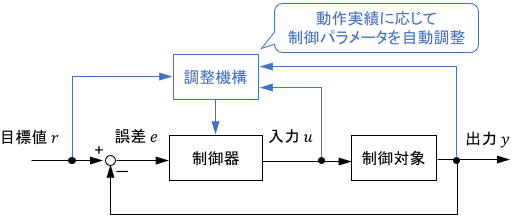
一方のセルフチューニングレギュレータは、数式モデルのパラメータを補正し、得られたモデルに基づいて制御器を設計し直す方法です。数式モデル経由で制御器を補正するため、間接法とも呼ばれます。

予見制御
予見制御(Preview Control)は、最適制御に将来を見越したフィードフォワード機能を持たせた手法です。「予見制御」というと、線形の最適制御を指す場合がほとんどです。
将来の目標値や外乱などが既知であるとして、それに基づいて普通の最適制御入力を補正するような入力を導出します。
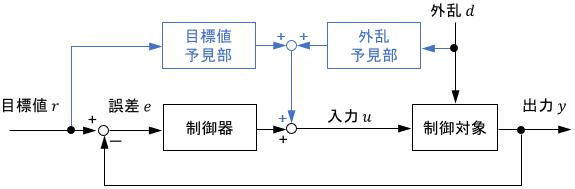
予見制御の利点としては、2自由度制御と同じくフィードバック制御とフィードフォワード制御の利点を両立できることが挙げられます。
ロバスト制御
ロバスト制御(Robust Control)は、数式モデルに含まれる「不確かさ」の範囲を考慮し、想定される最悪の場合でも安定した結果が得られるように制御する手法です。
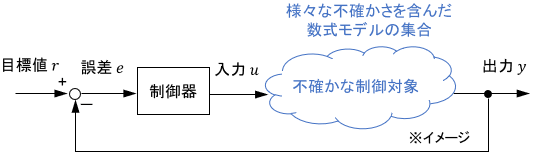
ロバスト制御以前では、「いかにモデルの誤差を低減し、完璧に近づけるか」が考えられてきました。ロバスト制御ではある意味それを諦め、「モデルが完璧でなくても大丈夫な制御」を考えます。
ロバスト制御の利点は、当然誤差や外乱などの不確かさに強いことです。ただし、数式モデルに加えて「不確かさ」を考慮する必要があるため、設計難度は高くなります。
さらに「常に最悪の場合を考える保守的な制御」とも言えるため、モデルが完璧である場合よりも制御性能は低くなります。
ロバスト制御の代表的な手法としては、H∞制御・μ解析・LMIを用いた手法が挙げられます。H∞制御は古典制御の図式的な設計方法と親和性が高いことから、古典制御でも用いられます。
モデル予測制御
モデル予測制御(Model Predictive Control)は、現在を開始点として、少し将来までの最適制御問題を制御中に解き続けることで「結果的」に最適フィードバック制御を実現する手法です。
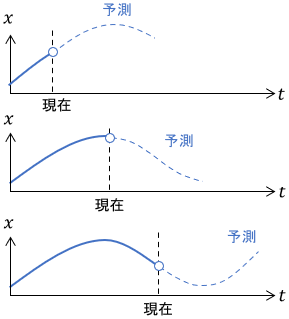
他の最適制御手法は、モデルに基づいて制御前に最適な制御則を求めます。一方でモデル予測制御は、最適な入力を制御中に求め続ける点が大きく異なります。
脳筋戦法に聞こえますが、「事前に網羅的な制御則を考えなくていい」というのは、問題を解く上で結構便利な性質です。
モデル予測制御の利点としては、まずフィードバック制御とフィードフォワード制御の利点を両立できることが挙げられます。これに加えて、制御中に目標軌道が変わっても対応できたり、入力や状態の制約を考慮できたりと、かなり実用性に優れることが知られています。
リアプノフ関数による制御
リアプノフの安定性解析を用いて、「状態や誤差を0に閉じ込める」イメージの制御手法です。基本的に非線形システムの制御に用いられます。
リアプノフの安定性解析とは、システム
$$\dot{x} = f(x)$$
に対し、
$$\begin{align} V(x) &\succ 0 \\ \dot{V}(x) &\prec 0\end{align}$$
を満たすリアプノフ関数$V(x)$があれば、システムは漸近安定である($\lim _{t\rightarrow \infty} x(t)= 0$を満たす)というものです。
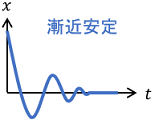
平たく言うと、時間とともに変数$x$が0に閉じ込められるわけですね。
ここでポイントなのは、$x$はシステムの状態に限定されず、何でも良いということです。たとえば$x$を「制御量と目標値の誤差」と設定すると、時間が経つに連れて誤差が0に収束し、追従制御を達成できることになります。
この場合、設計の流れは次のようになります。
- 誤差$x$に対する微分方程式$\dot{x} = f(x,u)$を立てる
- 誤差$x$に対するリアプノフ関数候補$V(x)\succ 0$を作る
- $\dot{V}(x)$を計算すると$\dot{x} = f(x,u)$が中に現れるので、$\dot{V}(x) \prec 0$が満たされるように制御入力$u$を設定する。
リアプノフの安定性解析は線形システム・非線形システム関係なく適用可能なので、適用範囲が非常に広いのが利点です。
一方、リアプノフ関数を試行錯誤的に探す必要があるのが欠点です。特に複雑なシステムでは、リアプノフ関数が手に負えないほど複雑になりがちなので、注意(覚悟)が必要です。
スライディングモード制御
スライディングモード制御(Sliding Mode Control)は、「システムの挙動をある軌道(面)に閉じ込める」イメージの制御手法です。リアプノフ関数による制御の発展版とも解釈できます。こちらも基本的に非線形システムの制御に用いられます。
まずシステム$\dot{x} = f(x,u)$に対し、閉じ込めたい軌道(面)を次の微分方程式の形で設計します。
$$S(x)=0$$
このとき、$S(x)$が状態空間上で張る面をスライディング面と呼びます。例えば次のような状態$x$に対して、次のようなスライディング面が設定できます。
$$ x = \left[ \begin{array} {c} p\\ \dot{p} \end{array} \right]$$
$$S(x) = \left[ \begin{array} {c c} 1 & 1 \end{array} \right]\left[ \begin{array} {c} p\\ \dot{p} \end{array} \right] = p + \dot{p} = 0$$

あとは$S(x)$に対するリアプノフ関数$V(S)$を設定し、それが$V(S) \succ 0$と$\dot{V}(S) \prec 0$を満たすように制御入力$u$を設定すれば、システムの挙動はスライディング面$S(x)=0$に閉じ込められます。
このときのシステムの挙動を状態空間上で表すと、まず状態がスライディング面に向う到達モードを経て、スライディング面上を”滑る”スライディングモードに遷移するようなものとなります。
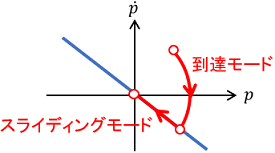
スライディングモード制御の強みとしては、ロバスト性に非常に優れること、すなわち数式モデルの誤差や外乱に強いことが挙げられます。ただし、スライディング面近傍でチャタリングが生じやすいため、何らかの対策が必要となります。
※システムの挙動をスライディング面に閉じ込める方法は、上記のリアプノフ関数による方法の他にも、様々なものが提案されています。
以上、メジャーな制御手法の一覧でした。それぞれの手法の開発の裏には物語(歴史)があります。気になる方は、こちらの記事をご参照ください。(面白いよ!)











コメント
初めまして。質問があります。よろしければお答えください。
記事内の「リアプノフ関数による制御」の個所で「リアプノフ関数を試行錯誤的に探す必要がある」と記載されていますが、試行錯誤的に探すとは具体的にどういう作業を行うのでしょうか?
例えば1次関数から高次の関数まで、係数を色々と変えてリアプノフ関数の定義に合うものを探してくるという感じなのでしょうか?
また、探す際のコツや、指針などがあれば教えて頂けないでしょうか?
どうぞよろしくお願い致します。
質問ありがとうございます。リアプノフ関数の探し方は取り扱う問題によって千差万別ですが、よくやる指針としては次の2つが挙げられます。
①とりあえず2次形式で試す
ベクトルx(t)に対する最もシンプルな正定関数は x^T A x という2次形式ですので、この形から試すことが多いです。これでダメなら、x(t)に対する何らかのベクトル関数Φ(x)を用いて Φ(x)^T A Φ(x) という形をつくり、これをベースに色々試行錯誤する、というイメージです。このアプローチは”Sum of Squares”と呼ばれており、先人によって色々研究されていますので、詳細はこのキーワードで調べてみると良いと思います。
②物理現象の前提知識から推測する
リアプノフ関数に求められる性質を超ざっくりと言うと「時間とともに0に向かって単調減少すること」であるので、そのような性質をもつ物理量をリアプノフ関数にしてみることも多いです。機械システムの例だと、摩擦を受けながら平面運動する物体を考える場合、その運動エネルギーは時間とともに0に向かって単調減少するので、運動エネルギーがリアプノフ関数となる(またはリアプノフ関数に含まれる)可能性が高いです。またこの場合、運動エネルギーは速度vに対する2次形式1/2*mv^2となりますが、この知見に習って別の「エネルギーっぽいもの」を設定してみることもあります。例えば速度でないパラメータaが時間とともに0になることが分かっていれば、aに関する「エネルギーっぽいもの」として2次形式1/2*na^2(nはmに変わる定数)を設定してみる、といったアプローチが考えられます。