このページでは、極と零点の意味・計算例・利点について解説します。
- 極と零点は、システムの特性がギューッと凝縮された便利なパラメータ
- 「伝達関数の分母＝0」として$s$について解いた解がシステムの極
- 「伝達関数の分子＝0」として$s$について解いた解がシステムの零点
- 面倒な逆ラプラス変換をすることなく、システムの応答を把握・分析できることが利点
極・零点とは
一般的に、システムの伝達関数は次のように分数の形で得られます。
$$G(s)=\frac{N(s)}{D(s)}$$
このとき、分母$D(s)=0$の根、つまり$D(s)=0$を$s$について解いた解をシステムの極と言います。この極を求める方程式$D(s)=0$は、特性方程式と呼ばれます。
同様に、分子$N(s)=0$の根、つまり$N(s)=0$を$s$について解いた解をシステムの零点と言います。
極と零点を一言で説明すると、システムの特性がギューッと凝縮された便利なパラメータです。
計算例と図式表現
それでは、具体的に極と零点を計算してみましょう。以下、３つのシステムを例題として説明していきます。
例１：実数の極・零点を持つシステム
まず、伝達関数が次式で表されるシステムを考えます。
$$G(s)=\frac{N(s)}{D(s)}=\frac{s+2}{s^2+13s+30}$$
伝達関数を変形すると
$$G(s)=\frac{N(s)}{D(s)}=\frac{s+2}{(s+3)(s+10)}$$
となりますね。分母\(D(s)=0\)と分子\(N(s)=0\)を解くことで、極と零点が次のように求まります。
$$\begin{array}{rrr} 極:& -3,&-10 \\ 零点:&-2\ & \end{array}$$
このように実数で表される極は、実極と呼ばれます。同様に実数で表される零点は「実零点」と呼ばれるはずですが、あまり聞いたことはありません（意味は通じますが）。
また、極と零点は、全てをひと目で把握するために複素平面上にプロットされることがあります。極は×、零点は○でプロットされることが慣例となっています。
今回の例をプロットすると、次のようになります。
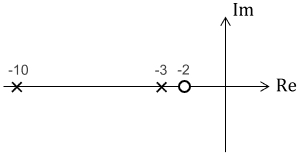
極・零点ともに実数なので、実軸上に点がならんでいますね。
例２：実数でない極・零点を持つシステム
次に、伝達関数が次式で表されるシステムを考えます。
$$G(s)=\frac{N(s)}{D(s)}=\frac{s^2-2s+10}{s^2+10s+26}$$
先ほどの例のようにスッキリと式変形するのは難しいので、分母$D(s)=0$と分子$N(s)=0$に2次方程式の解の公式を適用しましょう。極と零点は、次のように求まります。
$$\begin{array}{rrr} 極:& -5+j,&-5-j \\ 零点:&1+3j,&1-3j\end{array}$$
$j$は虚数単位です。このような実数でない極は、複素極と呼ばれます。同様に実数でない零点は「複素零点」と呼ばれるはずですが、こちらもあまり聞いたことはありません（意味は通じますが）。
※「複素数」は実数も虚数も含む用語なので、虚数の極を「複素極」と呼ぶのには違和感があるかもしれませんが、制御工学では慣例的にこのように呼ばれることが多いです。
この極と零点を複素平面上にプロットすると、次のようになります。
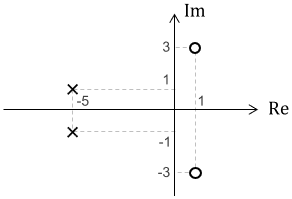
極・零点ともに実数でないため、点が複素平面全体に分布していますね。また、複素極・複素零点は常に共役なもの（虚部の±が異なるだけのもの）がセットで現れるため、プロットすると上下対象な形が得られます。
例３：零点がないシステム
最後に、伝達関数が次式で表されるシステムを考えてみます。
$$G(s)=\frac{N(s)}{D(s)}=\frac{1}{s^2-4s+8}$$
単純なシステムの伝達関数は、このように分子に$s$が現れない場合が多いです。分子に$s$が現れるのは数式モデルに入力の微分が含まれる場合ですが、そのようなシステムってあまりありませんよね。
このような伝達関数の場合、零点はありません。極は解の公式で求めましょう。
$$\begin{array}{rll} 極:& 2+2j,&2-2j \\ 零点:&なし& \end{array}$$
この極と零点を複素平面上にプロットすると、次のようになります。
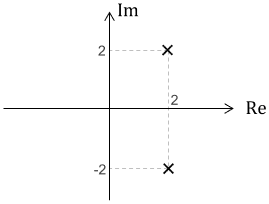
以上、３つの例を見てきました。極と零点を求めるには虚数を含む方程式を解く必要があり、手計算で求めるのはちょっと面倒でしたね…
でも安心してください。最近はコンピュータが一瞬で伝達関数から極と零点を計算してくれますので、実用上は導出にはほとんど困りません。そのかわり、理論的な理解をしっかりと深めておきましょう。
※例えばこちらのサイトでは、入力した伝達関数に対し、極・零点を含め様々な性質を自動で計算してくれます。
安定極・不安定極と安定零点・不安定零点
実極・複素極に関わらず、実部が負である極は安定極、そうでない極は不安定極と呼ばれます。同様に、実部が負である零点は安定零点、そうでない零点は不安定零点と呼ばれます。
※実部の正負はシステムの安定性に大きく影響を与えることから、このような名前が付いています（特に極は）。詳細はこちらのページをご覧ください
上の例で導出した極・零点を、安定なものと不安定なものに分類してみましょう。
$$\begin{array}{rrrl} 極:& -3,& -10 &\rightarrow 安定極 \\ 零点:& &-2 &\rightarrow 安定零点\\ 極:& -5+j,& -5-j &\rightarrow 安定極 \\ 零点:&1+3j,& 1-3j &\rightarrow 不安定零点\\極:& 2+2j,& 2-2j &\rightarrow 不安定極 \end{array}$$
こうして並べるとちょっとややこしく感じるかもしれませんが、複素平面上で確認すれば一発で判別できるので簡単です！
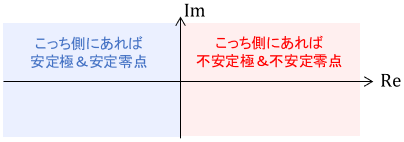
上の例のプロットと見比べてみてくださいね。
極・零点の利点
極と零点の最大の利点は、逆ラプラス変換をすることなく、システムの時間応答をある程度把握・分析できることです。
伝達関数の利点は、次のように、かけ算だけで微分方程式が解ける（出力が求まる）ことでした。
$$\usg{Y(s)}{出力} = \usg{G(s)}{伝達関数} \cdot \usg{U(s)}{入力}$$
※伝達関数についての詳細は、こちらのページをご覧ください
ここで得られる$Y(s)$は出力のラプラス変換なので、時間領域での出力$y(t)$を知るには$Y(s)\rightarrow y(t)$と逆ラプラス変換する必要があります。ただこの逆ラプラス変換、部分分数分解がたくさん出てきたりして、ちょっと面倒なんですよね…（微分方程式を直接解くよりはマシですが）。
そんなとき、極と零点に注目することで、逆ラプラス変換することなく、時間領域での出力$y(t)$の挙動をある程度把握する事ができます。例えば、振動が発生するかどうかや、システムが安定であるかどうかは、極と零点の情報からすぐに分かります。さすが情報が凝縮されているだけありますね！
極と零点からは他にも様々な情報を読み取ることができますが、なかなか奥が深いので、詳細はこちらの記事で個別に解説しています。合わせてご参照ください。
- 極と零点は、システムの特性がギューッと凝縮された便利なパラメータ
- 「伝達関数の分母＝0」として$s$について解いた解がシステムの極
- 「伝達関数の分子＝0」として$s$について解いた解がシステムの零点
- 面倒な逆ラプラス変換をすることなく、システムの応答を把握・分析できることが利点
コメント