このページでは、線形システム・非線形システムの違いと、時変システム・時不変システムの違いについて解説します。また、それぞれのシステムの具体例と、実用シーンでの使われ方についても解説します。
- 数式モデルが「係数×入出力(の微分)」の項だけで表されるものは線形システム、それ以外は非線形システム
- 係数が定数であるものは時不変システム、係数が時間に依存するものは時変システム
- 線形システムは扱いやすい、非線形システムは扱いにくい
- 時不変システムは扱いやすい、時変システムは扱いにくい
線形システムと非線形システム
数式モデルが「係数×入出力(の微分)」の項だけで表されるシステムを線形システム、それ以外のシステムを非線形システムと呼びます。入力を$u$、出力を$y$としたときの例を次に示します。
$$ \begin{alignat}{5} a_2 \ddot{y} &\ +\ a_1 \dot{y} & &\ +\ a_0 y & &=\ b_1 \dot{u} & &\ +\ b_0 u \ :& & \quad 係数×入出力(の微分)なので\textbf{線形}\\ a_2 \ddot{y} &\ +\ a_1 \dot{y} & &\ +\ a_0 \color{red}{\sin y }& &=\ b_1 \dot{u} & &\ +\ b_0 u\ :& & \quad \sin関数があるので\textbf{非線形} \\ a_2 \ddot{y} &\ +\ a_1 \color{red}{\dot{y}^2} & &\ +\ a_0 y & &= \ b_1 \dot{u} & &\ +\ b_0 u\ :& &\quad 2乗があるので\textbf{非線形} \\a_2 \ddot{y} &\ +\ a_1 \dot{y}^2& &\ +\ \color{red}{a_0 ^2} y & &=\ b_1 \dot{u} & &\ +\ b_0 u\ :& &\quad 係数は2乗しても係数のままなので\textbf{線形} \end{alignat} $$
線形システムは、式がシンプルで扱いやすいのが特徴です。入出力数が増えたり、微分の回数が増えたり、連立方程式になっても、線形でさえあれば厳密な解を求めることができます。
例えば下の式は、入力が2つ($u_1,u_2$)、出力が3つ($y_1,y_2,y_3$)の3階連立微分方程式です。複雑に見えますが、線形なので厳密解がしっかりと求まります。すごいですね!
$$ \left\{ \begin{array}{l} \dddot{y}_1 + \ddot{y}_1 + \dot{y}_2 + y_3 = \dot{u}_1 + u_2 \\ \dddot{y}_2 + \ddot{y}_2 + \dot{y}_3 + y_3 = \dot{u}_1 + u_1 \\ \dddot{y}_1 + \ddot{y}_3 + \dot{y}_3 + y_3 = \dot{u}_2 + u_2 \end{array}\right.$$
また、ここでは詳細を省きますが、線形システムは重ね合わせの原理に代表される便利な性質をさまざまに持っています。これらを用いることで、システムの特性を詳細に分析できることも大きな強みです。
一方で非線形システムは、線形システム以外を全てカバーする広い対応範囲が特徴です。ただし式が複雑なので、ほとんどの場合は厳密な解を求められません。

時変システムと時不変システム
線形システム・非線形システムは、係数の形式によって、さらに時変システムと時不変システムに分けられます。
具体的には、係数が定数であるものは時不変システム、係数が時間に依存するものは時変システムと呼ばれます。係数が1つでも時間に依存すれば、それは時変システムです。
$$ \begin{alignat}{5} a_2 \ddot{y} &\ +\ a_1 \dot{y} & &\ +\ a_0 y & &\ =\ b_1 \dot{u} & &\ +\ b_0 u\ : & &\quad 係数が定数なので\textbf{時不変} \\ a_2 \ddot{y} &\ +\ \color{red}{a_1(t)} \dot{y} & &\ +\ a_0 y & &\ =\ b_1 \dot{u} & &\ +\ b_0 u \ : & &\quad 係数が時間に依存するので\textbf{時変}\end{alignat} $$
線形システムは、時変であるか時不変であるかによって扱いやすさが結構変わります(時不変のほうが扱いやすい)。よってこれらを区別するために、それぞれを「線形時変システム」「線形時不変システム」と呼ぶこともあります。
※ちなみに、線形時不変システムのなかでも特に扱いやすいものを「プロパーなシステム」としてさらに区別することもあります。詳しくは、こちらのページをご覧ください
一方で非線形システムはもともと複雑なので、時変であるか時不変であるかによって扱いやすさはそこまで変わりません。よって「非線形時変システム」「非線形時不変システム」と区別して呼ぶことはそんなにありません。(意味は通じますが)
それぞれの扱いやすさのイメージをざっくり図で表すと、次のようになります。

線形時不変システムの例
例として、次のような機械システムを考えましょう。
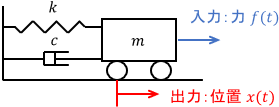
このシステムは、次のように線形時不変システムとしてモデリングできます。
$$ m\ddot{x} + c\dot{x} + kx = f $$
※こちらのページでは、その他の様々な線形時不変システムを紹介していますので、合わせてご覧ください
前述の通り、線形時不変システムは一番シンプルで扱いやすいので、まずこれを目指してモデリングが行われます。よって実用上は、線形システムのほとんどが時不変となります。なお、古典制御で扱うのは線形時不変システムのみです(ちょっぴりの例外を除いて)。
線形時変システムの例
先ほど説明した通り、線形システムのほとんどは時不変システムとしてモデリングされるので、線形時変システムが登場する機会は少なめです。ここでは、どのようなときに線形時変システムが使われるのかを解説します。
※少し詳細まで踏み込んだ説明をするため、線形システムと非線形システムの違いだけざっくり知りたい方は読み飛ばしても構いません。
線形時変な制御対象の例(ほとんどない)
先ほどの機械システムを再び考えましょう。

今、システムが動作するにつれてばねが徐々に温まり、それに応じてばね定数$k$が初期値$k_0$から$k_f$へ変化するとします。このシステムの運動方程式は、例えば次のように線形時変システムとして表すことができます。
$$ \begin{align}機械システムのモデル:&\quad m\ddot{x} + c\dot{x} + \color{red}{k(t)}x = f \\[3pt] ばね定数のモデル:&\quad \color{red}{k(t)} = (k_0 – k_f) e^{-t} + k_f \end{align}$$
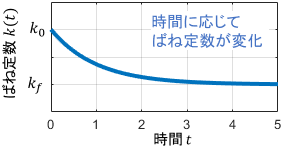
※式は一例なので、ここではイメージだけ抑えておけばOKです(以降も同じです)
ばね定数を時間の関数$k(t)$として、時間が経つにつれて(だいたい5秒かけて)変化するようにモデリングしているわけですね。このように、物理変数の変化を時間の関数として簡易的にモデリングすることが稀にあります。
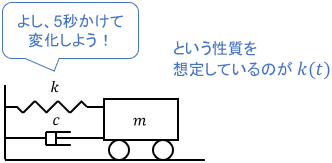
ただし、これは制御対象の本質を反映したモデリングにはなっていないことに注意してください。
実際のところ、ばね定数は時間に直接依存しているわけではありませんよね。本質的には、ばねの温度に依存しているわけです。よって周囲の気温など、動作条件が変わればその変化の様子も変わってしまい、上記モデルは使用できなくなってしまいます。
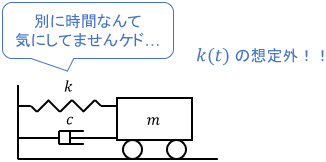
このような場合は、ばね定数を温度$\theta$の関数$k(\theta)$としてモデリングするほうが、本質的なモデルとなります。
$$ \begin{align}機械システムのモデル: & \quad m\ddot{x} + c\dot{x} + k(\theta)x = f \\[3pt] ばね定数のモデル(例):& \quad k(\theta) = a_1 \theta + a_0 \end{align}$$
ただしこの場合は、「温度$\theta$がどう変化するのか」を表すモデルが別途必要となるため、全体の式が多くて複雑になってしまいます。
このようにそれぞれに利点・欠点があるので、どのようにモデリングするかはケースバイケースで柔軟に判断する必要があります。そこが設計者の腕の見せ所でもありますが、基本的には物理変数を直接時間の関数とすることはほとんどないと考えてよいでしょう。
線形時変な制御器の例(たまにある)
一方で制御器は人が勝手に設計するものなので、制御の係数を時間の関数とする(つまり線形時変システムとする)ことはたまにあります。
例えば、制御を徐々に有効化/無効化する場合がこれにあたります。例として、次のような簡単な比例制御システムを考えましょう。

$K$は定数の制御ゲインで、制御対象は線形システムであるとします。今、制御開始直後にシステムが大きく暴れてしまい、それが問題となっているとしましょう。
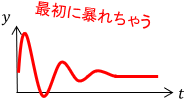
どうも制御をいきなりONにすることが暴れる原因のようです。よって、制御を徐々に有効化させることを考えましょう。これは、次のような時変の係数$w(t)$を制御器にかけることで実現できます。
$$w(t) = 1 – e^{-t}$$

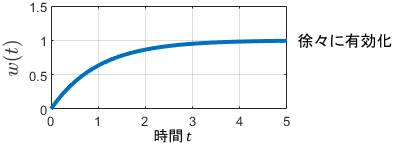
$w(t)$によって、だいたい5秒かけて徐々に制御が有効化されていますね。このとき、制御器は入力$e$、出力$u$の線形時変システムであると解釈できます。当然、制御器と制御対象をまとめたシステム全体も、線形時変システムとなりますね。
※ちなみに上記は、「ゲインスケジューリング」と呼ばれる制御の調整手法の一種だとも解釈できます
非線形システムの例
単純な非線形システムの例としては、振り子が挙げられます。
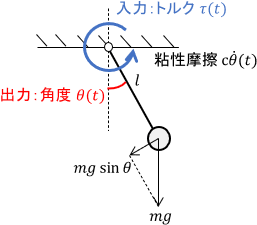
このシステムは、次のように非線形な運動方程式で表されます。
$$ml^2 \ddot{\theta} + c \dot{\theta} + mgl \ubg{\sin \theta }{非線形} = \tau$$
ちなみに入出力以外の係数が全て定数なので、これは時不変なシステムです。
前述の通り、非線形システムは厳密な解を求めることが難しいため、制御するには工夫が必要となります。非線形制御理論では、例えば次のようなアプローチが取られます。
- コンピュータ計算により強引に解を求める(例:数値計算)
- 厳密解は分からなくとも、制御量だけは無理やり一定値に収束させる(例:リアプノフ関数を用いた制御)
またテイラー展開などを用いて、非線形システムを扱いやすい線形システムに近似することもよく行われます。これにより、精度は下がりますが厳密解が求まり、線形の制御理論を適用することが可能となります。
$$\begin{gather} \sin \theta \approx \theta と近似して、 \\[5pt] ml^2 \ddot{\theta}+ c \dot{\theta} + mgl \theta = \tau \quad \color{green}{線形になった!}\end{gather}$$
※テイラー展開とそれを用いた近似についてはこちらのページで詳しく説明していますので、合わせてご覧ください
以上、線形システム・非線形システムの違いと、時変システム・時不変システムの違いについての解説でした。
式の形だけでなく、上で説明したような実用上の使い方もイメージしておくと便利ですので、頭の片隅に置いておいてくださいね。
- 数式モデルが「係数×入出力(の微分)」の項だけで表されるものは線形システム、それ以外は非線形システム
- 係数が定数であるものは時不変システム、係数が時間に依存するものは時変システム
- 線形システムは扱いやすい、非線形システムは扱いにくい
- 時不変システムは扱いやすい、時変システムは扱いにくい






コメント