このページでは、伝達関数の定義と利点について、具体例を挙げながら解説します。また、伝達関数を扱う際に入力・出力の初期値を0と考えていい理由についても解説します。
- 伝達関数は、ラプラス変換の結果得られる、システムの入出力特性を表す関数
- 「出力=伝達関数×入力」とかけ算だけで入出力関係を表せるので、取扱いが超簡単
- 伝達関数をちょっと変形すると周波数伝達関数になり、簡単に周波数解析ができる
- 入出力(とその微分)の初期値を0と仮定する場合が多いが、実用上はそれでほとんど問題ない
伝達関数の概要
伝達関数とは、システムの入出力特性を表す、古典制御の基礎となる関数のことです。順番に詳細を見ていきましょう。
一般的に、動的システムの数式モデルは微分方程式で表されます。システムが複雑になると、当然微分方程式も複雑になり、その解析が難しくなります。
そこで古典制御では、ラプラス変換という変数変換を用いて、システムの数式モデルを扱いやすい形式に変換します。こうして得られるもの(数式モデルをラプラス変換したもの)が、伝達関数です。
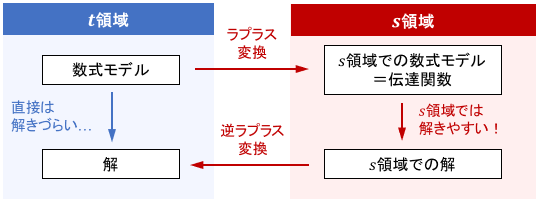
※ラプラス変換の詳細については、こちらのページをご覧ください
伝達関数の例
具体例で確認していきましょう。次のような機械システムを考えます。
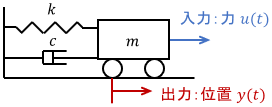
システムの入力は台車に加わる力$u(t)$、出力は台車の位置$y(t)$です。このシステムの数式モデルは、次の通り運動方程式で表されます。
$$m\ddot{y} + c\dot{y} + ky = u$$
最初に台車が平衡状態で静止している、つまり$y(0)=\dot{y}(0)=0$であるとして、これをラプラス変換してみましょう。$u(t)$、$y(t)$をラプラス変換したものをそれぞれ$U(s)$、$Y(s)$で表すと、次式が得られます。
$$ms^2Y(s) + csY(s) + kY(s) = U(s)$$
出力についてまとめると、次のようになりますね。
$$Y(s)=\ubg{\frac{1}{ms^2 + cs + k}}{G(s)とする} U(s)=G(s)\cdot U(s)$$
ラプラス変換後の世界(\(s\)領域)では、出力が「関数$G(s)$×入力$U(s)$」の形で表されました。この入力と出力をつなぐ関数$G(s)$が伝達関数というわけです。
$$\usg{Y(s)}{出力} = \usg{G(s)}{伝達関数} \cdot \usg{U(s)}{入力} $$
この伝達関数の利点について、詳しく見ていきましょう。
伝達関数の利点
利点1:微分方程式が、かけ算で解けるようになる!
先ほどの例の通り、伝達関数を用いることで、システムの出力を伝達関数と入力のかけ算だけで求められるようになります。
通常、微分方程式を解こうとすると面倒な積分操作が必要となりますが、それがかけ算だけになると嬉しいですよね。高階の微分方程式もかけ算だけで解けるので、システムが複雑になるほどこの恩恵も大きくなると言えます。
$$y^{(4)}+a_3 y^{(3)}+ a_2 y^{(2)}+ a_1 y^{(1)} +a_0 y = b_1 u^{(1)} + b_0 u$$
$$Y(s) =\ubg{ \frac{b_1 s + b_0}{s^4 + a_3 s^3 + a_2 s^2 + a_1 s + a_0}U(s)}{微分が多くても、かけ算だけで出力(解)が求まる!}$$
もちろん伝達関数によって得られる$Y(s)$は$s$領域での解ですが、これを$Y(s)\rightarrow y(t)$と逆ラプラス変換することで、$t$領域での解$y(t)$が得られます。
※ラプラス変換を用いた微分方程式の解き方については、こちらのページで詳しく解説しています
また、伝達関数の極や零点というパラメータを見ることで、わざわざ逆ラプラス変換をしなくても$y(t)$の挙動をある程度分析することもできます。このお手軽さが伝達関数の大きな利点です。
※極と零点については、こちらのページをご覧ください
利点2:簡単にシステムを結合できる!
先ほどのシステムでは入力である力$u$を自由に操作できると仮定していました。今度は、下図のようにプロペラの風で力を発生させるとしましょう。
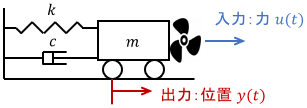
このとき、プロペラの特性も含めたシステムの特性を考えてみましょう。プロペラは入力電流$i$に応じて風力$u$を発するもので、その特性は次の微分方程式で表されるとします。
$$\ddot{u} + a_1 \dot{u} + a_0 u= i$$
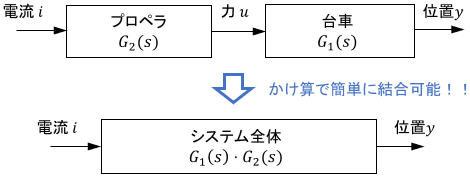
ブロック線図にすると次の通りですね。

よって台車の動作$y$を得るためには、まずプロペラの微分方程式を解き、さらにその解$u$を入力として台車の微分方程式を解く必要があります。
もちろんそのような計算は可能ですが、面倒な上にシステム全体の特性の見通しが悪いですよね。これよりもさらに複雑なシステムだとなおさらです。
伝達関数を使うと、このような場合も超簡単に対応できます。$s$領域では入出力がかけ算の関係になるので、$i$から$y$までのシステム全体の入出力特性も、次のように伝達関数どうしのかけ算で得られます。
$$\begin{align}台車の特性:Y(s)&=\frac{1}{ms^2 + cs + k}U(s)\\ \\プロペラの特性:U(s) &=\frac{1}{s^2 + a_1s + a_0}I(s) \qquadなので、\\\\ 全体の特性:Y(s)&=\ubg{\frac{1}{ms^2 + cs + k}}{台車の伝達関数G_1(s)} \cdot \ubg{\frac{1}{s^2 + a_1s + a_0}}{プロペラの伝達関数G_2(s)} I(s)\end{align}$$
利点3:簡単に周波数解析ができる!
ラプラス変換は周波数解析と非常に相性が良いため、伝達関数を用いて簡単にシステムの周波数解析を行うことができます。
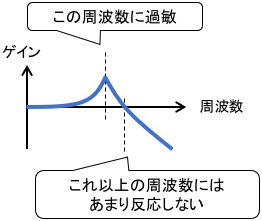
周波数解析は、「システムが様々な周波数の信号成分に対してどのように反応するか」を解析する手法です。(周波数は「信号の変化の速さ」だと思ってください)
これにより、考慮しているシステムに対して「この周波数の信号成分に特に過敏に反応する」とか「これ以上の周波数にはあまり反応しなくなる」といった情報を知ることができます。
話を伝達関数に戻しましょう。今、周波数を$\omega$、虚数単位を$j$とします。このとき、伝達関数$G(s)$に$\omega j$を入れた$G(\omega j)$が、そのままシステムの周波数特性(システムのフーリエ変換)となることが知られています。この$G(\omega j)$は、周波数伝達関数と呼ばれます。
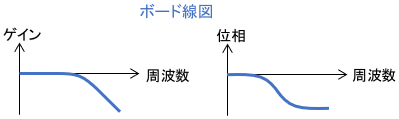
この周波数伝達関数を用いることで、手軽に周波数解析を行うことができます。例えば、周波数伝達関数をグラフに描くことでボード線図やベクトル軌跡が得られ、システムの周波数特性を視覚的に確認できます。
※周波数解析についてはこちらのページで解説していますので、合わせてご覧ください。
初期値を0としていい理由
古典制御では、入出力(とその微分)の初期値が全て0であると仮定してシステムを取り扱うことがほとんどです。ここまでの例でも、そのように仮定していましたね。
なぜこんな仮定を置くかというと、関数の微分のラプラス変換が、次のように非常にシンプルで取り扱いやすい形になるからです。
$$\begin{alignat}{2}\dot{f}(t) &\ \xrightarrow{\large ラプラス変換}\ sF(s) – f(0) &&= sF(s) \\[3px] \ddot{f}(t) &\ \xrightarrow{\large ラプラス変換}\ s^2 F(s) -sf(0) – \dot{f}(0) &&= s^2 F(s)\end{alignat}$$

…勝手にそんな仮定を置いていいの?適用範囲が狭まらないの?
と思うかもしれませんが、実際はそこまで問題にならないことがほとんどです。この理由を説明していきます。
理由1:実際に初期値0の場合がほとんどだから
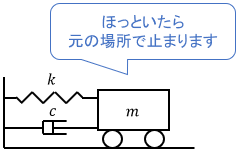
ほとんどのシステムにおいて、初期値が0であるとは「最初にシステムが停止している」か「最初にシステムが平衡点にある」ことを指します。大抵のシステムはこのどちらかの状態から動き出すので、実際に初期値が0である場合がほとんどです。
例えば機械システムであれば、スイッチがOFFになっていて(釣り合いの位置で)止まっている状態のイメージですね。当然、この状態からスイッチをONにして動かすわけです。
もしシステムが動いている状態でも、スイッチを切れば簡単に初期値0にリセットできるので、実用上は初期値を0に固定してもほとんど困りません。
理由2:初期値が何であれ伝達関数は変わらないから
もし実際の初期値が0でない場合、計算の結果得られる出力\(Y(s)\)は現実の動作と異なってしまいます。このような場合でも、制御器設計という観点でいえば問題ないことがほとんどです。具体的に説明していきましょう。
古典制御における制御器設計は、「出力が具体的にどうなるか」ではなく「入力が出力にどう影響を与えるか」という入出力の関係性に基づくものがほとんどです。例えば先ほど紹介した周波数解析は、具体的な出力の挙動ではなく、入出力の関係性を分析する手法ですよね。
そして、この入出力の関係性を表すものが伝達関数でしたが、伝達関数は初期値が何であれ変わりません。よって初期値の設定がちょっとくらい現実と異なっていても、適切に制御器を設計できる場合がほとんどです。
例として、先ほどの機械システムをもう一度考えましょう。

$$m\ddot{y} + c\dot{y} + ky = u$$
初期値$y(0),\dot{y}(0)$を0としないで運動方程式をラプラス変換してみます。
$$m\bigl\{ s^2Y(s) -sy(0) – \dot{y}(0) \bigr\} + c\bigl\{ sY(s) – y(0)\bigr\} + kY(s) = U(s)$$
出力についてまとめると、次のようになります。
$$Y(s)= \ubg{\frac{1}{ms^2 + cs + k}}{G(s)} \Bigl[ U(s) + \ubg{\vphantom{ \frac{1}{ms^2 + cs + k} }m\bigl\{ sy(0) + \dot{y}(0)\bigr\} + dy(0)}{初期値に関する情報➔I(s)} \Bigr]$$
初期値に関する情報を$I(s)$とまとめると、入力$U(s)$と初期値情報$I(s)$はそれぞれ独立に出力$Y(s)$に作用することがわかります。
$$\begin{align}\osg{Y(s)}{出力} &= \osg{G(s)}{伝達関数} \Bigl\{ \osg{U(s)}{入力} + \osg{I(s)}{初期値} \Bigr\} \\[3pt] &= G(s)U(s) + G(s) I(s) \end{align}$$
よって、初期値が0でない場合も入出力の関係性は変わらず伝達関数$G(s)$で表されます。言い換えると、「結局無視する初期値の項を最初から考えないために、初期値を0に設定している」とも解釈できますね。
以上、伝達関数とその利点、初期値の考え方についての解説でした!こちらの記事では、伝達関数の具体例を数多く紹介していますので、あわせてご覧ください。
- 伝達関数は、ラプラス変換の結果得られる、システムの入出力特性を表す関数
- 「出力=伝達関数×入力」とかけ算だけで入出力関係を表せるので、取扱いが超簡単
- 伝達関数をちょっと変形すると周波数伝達関数になり、簡単に周波数解析ができる
- 入出力(とその微分)の初期値を0と仮定する場合が多いが、実用上はそれでほとんど問題ない








コメント