このページでは、実用場面でよくでてくる高次系の伝達関数を、導出過程を含めて紹介します。
高次系は、シンプルなシステムを複数組み合わせた形をしていることが多いです。高次系の基本的なイメージについては、こちらの記事をご覧ください。
倒立振子
まずは、機械システムを2つ組み合わせた例として倒立振子を紹介します。倒立振子にも色々種類があるのですが、下図のように台車の上に振り子を乗せたものは台車駆動型倒立振子と呼ばれ、機械制御の例題として非常によく用いられます。
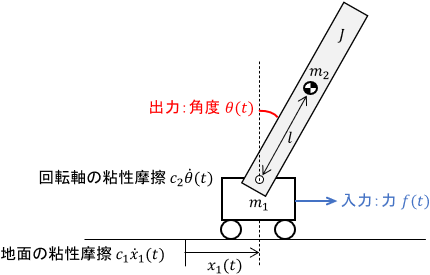
入力は台車に加わる力$f(t)$、出力は振り子の角度$\theta (t)$、$x_1(t)$は台車の位置、$m_1,m_2$はそれぞれ台車と振り子の質量、$c_1,c_2$はそれぞれ地面と回転軸の粘性摩擦係数、$J$は振り子の重心周りの慣性モーメントです。
ラグランジュの方法を用いて、このシステムの運動方程式を導出していきます。まず下準備として、振り子の重心位置$x_2(t),y_2(t)$と重心速度$\dot{x}_2(t),\dot{y}_2(t)$を振り子の角度$\theta(t)$を用いて表します。
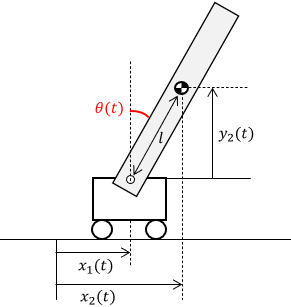
$$\begin{array}{lll} x_2 = x_1 + l \sin \theta & & y_2 = l \cos \theta \\ \dot{x} _2 = \dot{x}_1 + l \dot{\theta} \cos \theta & & \dot{y}_2 = – l \dot{\theta} \sin \theta \end{array}$$
これらを用いながら、台車・振り子それぞれの運動エネルギーとポテンシャルエネルギーを導出すると、次式が得られます。
$$\begin{align} 台車の運動エネルギー\ T_1&=\frac{1}{2}m_1 \dot{x}_1 \\[5pt] 振り子の運動エネルギー\ T_2&= \frac{1}{2} J \dot{\theta}^2 + \frac{1}{2} m_2 ( \dot{x}_2 ^2 + \dot{y}_2 ^2) \\[5pt] &= \frac{1}{2} J \dot{\theta}^2 + \frac{1}{2} m_2 ( \dot{x}_1 ^2 + l^2 \dot{\theta}^2 + 2 l \dot{x}_1 \dot{\theta} \cos \theta)\\[5pt] 台車のポテンシャルエネルギー\ U_1 &= 0 \\[5pt] 振り子のポテンシャルエネルギー\ U_2 &= m_2 g y_2 = m_2 g l \cos \theta \end{align}$$
これらより、このシステムのラグランジアンが次式で表されます。
$$\begin{align} L &= T_1 + T_2 – U_1 – U_2\\[5pt] &= \frac{1}{2}m_1 \dot{x}_1 + \frac{1}{2} J \dot{\theta}^2 + \frac{1}{2} m_2 ( \dot{x}_1 ^2 + l^2 \dot{\theta}^2 + 2 l \dot{x}_1 \dot{\theta} \cos \theta) – m_2 g l \cos \theta \end{align}$$
また、粘性摩擦を考慮するための散逸関数も導出しておきます。
$$\begin{align} 台車の散逸関数\ D_1 &= \frac{1}{2} c_1 \dot{x}_1^2\\[5pt] 振り子の散逸関数\ D_2 &= \frac{1}{2} c_2 \dot{\theta}^2 \end{align}$$
これらを用いて次式を計算することで、台車と振り子の運動方程式を導出できます。
$$ \left\{ \begin{array}{ll} \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}_1} \right) – \frac{\partial L}{\partial x_1} + \frac{\partial D}{\partial \dot{x}_1} = f &\cdots 台車の運動方程式\\[5pt] \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{\theta}} \right) – \frac{\partial L}{\partial \theta} + \frac{\partial D}{\partial \dot{\theta}} = 0 &\cdots 振り子の運動方程式 \end{array} \right. $$
具体的に計算すると、次のようになります。
$$ \left\{ \begin{array}{l} (m_1 + m_2) \ddot{x}_1 + m_2 l \ddot{\theta} \cos \theta – m_2 l \dot{\theta}^2 \sin \theta + c_1 \dot{x}_1 = f\\[5pt] (m_2 l^2 + J) \ddot{\theta} + m_2 l \ddot{x}_1 \cos \theta – m_2 g l \sin \theta + c_2 \dot{\theta} = 0 \end{array} \right. $$
いま$\theta=0$近傍の運動のみ考えるとし、$\sin \theta \approx 0, \cos \theta \approx 1, \dot{\theta}^2 \approx 0$と近似すると、運動方程式は次のように単純化されます。
$$ \left\{ \begin{array}{l} (m_1 + m_2) \ddot{x}_1 + m_2 l \ddot{\theta} + c_1 \dot{x}_1 = f\\[5pt] (m_2 l^2 + J) \ddot{\theta} + m_2 l \ddot{x}_1 – m_2 g l \theta + c_2 \dot{\theta} = 0 \end{array} \right. $$
※$\theta=0$まわりで、テイラー展開を用いた1次近似を行っています。テイラー展開については、こちらのページをご覧ください
$x_1(t),\theta(t),f(t)$をラプラス変換したものをそれぞれ$X_1(s),\Theta(s),F(s)$として、上式をラプラス変換します。(以降、簡単のため$(s)$は省略します)
$$ \left\{ \begin{array}{l} (m_1 + m_2) s^2 X_1 + m_2 l s^2 \Theta + c_1 s X_1 = F\\[5pt] (m_2 l^2 + J) s^2 \Theta + m_2 l s^2 X_1 – m_2 g l \Theta + c_2 s \Theta = 0 \end{array} \right. $$
これらの方程式をまとめて、システム全体の伝達関数(入力$F(s)$から出力$\Theta(s)$までの伝達関数)を導出しましょう。1つ目の式を整理すると、次式が得られます。
$$ sX_1 = \frac{1}{(m_1 + m_2)s + c_1} (F – m_2 l s^2 \Theta) $$
これを2つ目の式に代入して整理すると、伝達関数が得られます。
$$ \Theta = \ubg{\frac{-m_2 l s}{\bigl\{ (m_1 + m_2)s + c_1 \bigr\} \bigl\{ (m_2 l^2 + J)s^2 + c_2 s – m_2 gl\bigr\} – m_2 ^2 l^2 s^3 }}{伝達関数} F $$
分母を$s$について整理すると、次式となります。
$$ {\small \Theta = \frac{-m_2 l s}{\bigl\{ m_1 m_2 l^2 + (m_1 + m_2)J \bigr\}s^3 + \bigl\{ c_1(m_2 l^2 + J) + c_2(m_1 + m_2) \bigr\}s^2 + \bigl\{ c_1 c_2 – (m_1 + m_2) m_2 gl \bigr\}s – c_1 m_2 gl } F }$$
$s$の次数が3なので、全体は3次系となっていることが分かりますね。
ちなみに粘性摩擦がない場合の伝達関数は、$c_1=c_2=0$とすることで次のように少しスッキリした形で求まります。
$$ \Theta = \frac{-m_2 l }{\bigl\{ m_1 m_2 l^2 + (m_1 + m_2)J \bigr\}s^2 – (m_1 + m_2) m_2 gl } F $$
DCサーボモーター
次に、電気システムと機械システムの組み合わせの例を見てみましょう。このようなシステムは、メカトロ系・メカトロシステムとも呼ばれます。ここでは、次のようなDCサーボモーター(直流サーボモーター)を考えます。

入力は電圧$v(t)$、出力はモーター回転角度$\theta (t)$、$i(t)$は回路を流れる電流、$R$は抵抗値、$L$はコイルのインダクタンス、$\tau(t)$はモーターが生み出すトルク、$K$はモーターの逆起電力係数、$M$はモーターのトルク係数、$J$はモーターにつながれた回転体の慣性モーメント、$c$は粘性摩擦係数です。
まず電気システムの方程式を導出します。回路中、それぞれの要素に加わる電圧は次のように計算できます。
$$\begin{align} 抵抗両端の電圧&:Ri \\[3pt] コイル両端の電圧&:L\dot{i} \\[3pt] モーター両端の電圧&:K \dot{\theta} \end{align}$$
モーター両端の電圧は、モーターの回転により生じる逆起電力を表しています。キルヒホッフの法則より、各電圧の関係は次のように表されます。
$$電気システムの方程式:\ v = Ri + L\dot{i} + K \dot{\theta}$$
続いて機械システムの方程式を考えます。回転体の運動方程式は次のように求められます。
$$ J \ddot{\theta} = -c \dot{\theta} + \tau$$
モーターから発生するトルクは電流に比例し、$\tau = M i$と表されます。よって上記運動方程式は、次のように書き換えられます。
$$機械システムの方程式:\ J \ddot{\theta} = -c \dot{\theta} + M i$$
まとめるとこうですね。
$$ \left\{ \begin{array}{ll}v = Ri + L\dot{i} + K \dot{\theta}& \cdots 電気システムの方程式 \\[3pt] J \ddot{\theta} = -c \dot{\theta} + M i& \cdots 機械システムの方程式\end{array} \right. $$
$v(t),i(t),\theta(t)$をラプラス変換したものをそれぞれ$V(s),I(s),\Theta(s)$として、上式をラプラス変換します。
$$ \left\{ \begin{array}{l}V = RI + LsI + K s \Theta\\[3pt] J s^2 \Theta = -c s\Theta + M I\end{array} \right. $$
これらの式から、システム全体の伝達関数(入力$V(s)$から出力$\Theta(s)$までの伝達関数)を導出しましょう。まず、2つ目の式を$I(s)$についてまとめます。
$$ I = \frac{1}{M} ( Js^2\Theta + cs\Theta )$$
これを1つ目の式に代入します。
$$\begin{align} V &=\frac{R}{M} ( J s^2\Theta + c s \Theta ) + \frac{L}{M} ( J s^3\Theta + c s^2\Theta ) + K s \Theta \\\\ &= \frac{1}{M} \Bigl\{ LJs^3 + (RJ+Lc)s^2 + (Rc + MK) s \Bigr\}\Theta \end{align}$$
あとは出力についてまとめると、伝達関数が得られます。
$$ \Theta = \ubg{ \frac{M}{ LJ s^3 + (RJ+Lc) s^2 + (Rc + MK) s}}{伝達関数} V$$
$s$の次数が3なので、電気システムと機械システムの組み合わせによって全体は3次系となっていることが分かりますね。また、伝達関数の分母が$s$でくくれるので、システムの極の1つは0であることが分かります。
※システムの極については、こちらのページをご覧ください
2自由度ばねダンパ系
最後にもう1つ、機械システムを2つ組み合わせた例として、次のばねダンパ系を考えます。
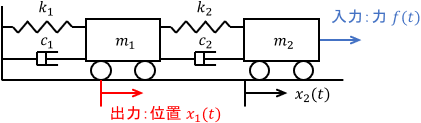
入力は台車2に加わる力$f(t)$、出力は台車1の位置$x_1(t)$、$m_1,m_2$は台車の質量、$k_1,k_2$はばね定数、$c_1,c_2$は粘性係数です。それぞれの台車の運動方程式は、次のように求まります。
$$ \left\{ \begin{array}{ll} m_1 \ddot{x}_1 = – k_1 x_1 – c_1 \dot{x}_1 – k_2 (x_1 – x_2) – c_2 (\dot{x}_1 – \dot{x}_2)& \cdots 台車1の運動方程式 \\[5pt] m_2 \ddot{x}_2 = k_2 (x_1 – x_2) + c_2 (\dot{x}_1 – \dot{x}_2) + f & \cdots 台車2の運動方程式\end{array} \right. $$
$x_1(t),x_2(t),f(t)$をラプラス変換したものをそれぞれ$X_1(s),X_2(s),F(s)$として、運動方程式をラプラス変換します。
$$ \left\{ \begin{array}{l} m_1 s^2 X_1 = – k_1 X_1 – c_1 s X_1 – k_2 (X_1 – X_2) – c_2 s(X_1 – X_2) \\[5pt] m_2 s^2 X_2 = k_2 (X_1 – X_2) + c_2 s (X_1 – X_2) + F\end{array} \right. $$
これらの方程式をまとめて、システム全体の伝達関数(入力$F(s)$から出力$X_1(s)$までの伝達関数)を導出しましょう。2つ目の式を整理すると、次式が得られます。
$$ X_2 = \frac{1}{m_2 s^2 + c_2 s + k_2} \Bigl\{ ( c_2 s + k_2) X_1 + F\Bigr\}$$
これを1つ目の式に代入して整理すると、伝達関数が得られます。
$$ X_1 = \ubg{ \frac{c_2 s + k_2}{\Bigl\{ m_1 s^2 + (c_1 + c_2)s + (k_1 + k_2)\Bigr\} (m_2 s^2 + c_2 s + k_2) – (k_2 + c_2 s)^2} }{伝達関数} F$$
分母を$s$について整理すると、次のようになります。
$$ {\small X_1 = \frac{c_2 s + k_2}{ m_1 m_2 s^4 + \bigl\{m_2 c_1 + (m_1+m_2) c_2\bigr\} s^3 + \bigl\{ m_2 k_1 + (m_1+m_2) k_2 + c_1 c_2 \bigr\}s^2 + (c_1 k_2 + c_2 k_1)s + k_1 k_2} F}$$
$s$の次数が4なので、4次系であることが分かりますね。ばねやダンパがない場合は、$k$や$c$を0にすればOKです。
以上、高次系の伝達関数例まとめでした!






コメント