このページでは、制御工学でよくでてくる「プロパーなシステム」・「プロパーな伝達関数」の意味とイメージを解説します。
※伝達関数の基本を未学習の方は、まずこちらの記事をご覧ください。
- 伝達関数が「分子の次数≦分母の次数」を満たすシステムを「プロパーなシステム」と呼ぶ
- プロパーなシステムは、現実世界で厳密な実現が可能である
- プロパーでないシステムは、現実世界で厳密な実現が不可能である
- ただし、システムがプロパーでなくても「ほぼ等しいシステム」で代替できることが多い
「プロパー」の定義
ある線形なシステムが、次の伝達関数で表されるとします。
$$G(s)=\frac{N(s)}{D(s)}$$
このとき「分子$N(s)$の次数≦分母$D(s)$の次数」であるなら、$G(s)$は「プロパーな伝達関数」と呼ばれます。(次数は「$s$が最大で何乗されているか」です)
さらに、プロパーな伝達関数の中でも「分子の次数<分母の次数」である伝達関数を特に区別して「厳密にプロパーな伝達関数」と呼ぶこともあります。
また、プロパーな伝達関数を持つシステムは、「プロパーなシステム」と呼ばれます。
古典制御で取り扱うシステムのほとんどは、プロパーです。
プロパーなシステムの例
シンプルな例として、微分方程式が次式で表されるシステムを考えましょう。
$$\ddot{y} + \dot{y} + y = \dot{u} + u$$
これをラプラス変換して伝達関数$G(s)$を求めると、次のようになりますね。
$$Y(s) = \ubg{\frac{s+1}{s^2 + s + 1}}{G(s)}U(s)$$
伝達関数の分母の次数は2、分子の次数は1なので、このシステムはプロパーであることがわかります。結局、
- 分母の次数=微分方程式内で出力を微分する回数
- 分子の次数=微分方程式内で入力を微分する回数
なので、微分方程式が「入力を微分する回数≦出力を微分する回数」を満たすシステムはプロパーであるとも言えます。
ちなみに、$y=Ku$のような比例関係で表されるシステムもプロパーです。伝達関数は$K$(定数)で、分母・分子ともに次数が0だからですね。
「プロパー」の直感的意味


ほーん。数式は分かったけど、「プロパーである」って結局どういうイメージなの?
一言で説明すると、プロパーな伝達関数は現実世界で厳密な実現が可能、プロパーでない伝達関数は現実世界で厳密な実現が不可能、という性質を持ちます。これについて、詳しく見ていきましょう。
まず、「プロパーでない伝達関数は、なぜ厳密な実現が不可能なのか」を考えたほうがわかりやすいので、それから説明します。シンプルな例として、微分方程式が次式で表されるシステムを考えましょう。
$$\dot{y} + y = \ddot{u} + \dot{u} + u$$
これをラプラス変換して伝達関数$G(s)$を求めると、次のようになりますね。
$$Y(s) = \ubg{\frac{s^2 + s+1}{s + 1}}{G(s)} U(s)$$
分母の次数は1、分子の次数は2なので、このシステムはプロパーではありません。これをさらに整理すると次のようになります。
$$\begin{align}Y(s) &= \frac{s^2 + s+1}{s + 1}U(s) \\\\ &= \frac{s(s+ 1)+1}{s + 1} U(s) \\\\ &=\biggl( \ubgd{ \vphantom{ \frac{1}{s+1} } s}{プロパー}{でない項} \ + \ \ubgd{\frac{1}{s+1}}{プロパー}{な項}\biggl) U(s)\end{align}$$
式を整理することで、プロパーでない伝達関数を「プロパーでない項」と「プロパーな項」に分けることができました。さらに展開すると、システムの出力$Y(s)$が、次式で得られます
$$Y(s) = \ubg{sU(s)}{入力の時間微分} + \frac{1}{s + 1}U(s)$$
この例のように、プロパーでないシステムは、プロパーでない項の作用で入力の時間微分(またはn階時間微分)を出力に含みます。この時間微分が、現実世界での実現を妨げる元凶です。


入力を微分して出力するだけなら簡単じゃないの?
と思うかもしれませんが、厳密な時間微分は現実世界で実現不可能なんです。
微分の定義をおさらいしましょう。時刻$t$における関数$f(t)$の導関数は、次で表されます。
$$\dot{f}(t) = \lim _{\Delta t \rightarrow 0} \frac{f(t+\Delta t) – f(t)}{\Delta t}$$
極限が付いているとはいえ、$f(t+\Delta t)$という未来の時刻の情報が必要となるのがポイントです。当然未来の情報を得る方法はありませんので、「厳密な」時間微分は実現不可能だというわけです。
というわけで、プロパーでない伝達関数は現実世界で厳密な実現が不可能です。一方、プロパーな伝達関数は上記のような問題が生じないので厳密な実現が可能となります。
プロパーかどうかを気にすべきタイミング
実現不可能では困るので、システムがプロパーであることは非常に重要です。ただし、システムがプロパーであるかどうかを気にすべきタイミングは、結構限られています。
まず、制御対象が現実世界のシステム(物理現象)である場合、それがプロパーであるかどうかを気にする必要はありません。現実世界のシステムは絶対にプロパーだからです。実現不可能なら存在しませんからね。
一方で、人間が設計(設定)したシステムがプロパーであるかどうかは気にするべきです。例えば制御器は人間が勝手に設計したシステムなので、プロパーでなくなる場合があります。
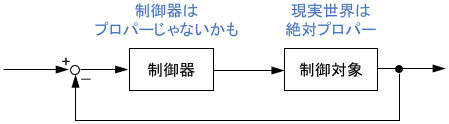

具体例として、PD制御器は誤差(制御器への入力信号)の微分操作を含むためプロパーでなく、厳密な実現は不可能です。
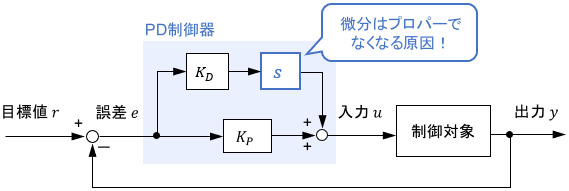



え、でもPD制御って現実に使われてるんじゃないの?
その通りです。実際のところは、プロパーでない制御器も微分要素を「厳密でないけどほぼ微分な要素」に置き換えることで、むりやり実現できる場合が多いです。
電気信号を微分する微分回路や、微分をプログラムで近似的に計算する数値微分がその代表でしょう。これらには必ず誤差が含まれるので「厳密な微分」ではないですが、実用上はそれで十分な場合がほとんどです。
※こちらのページでは、「厳密ではないけどほぼ微分な要素」の伝達関数の例を紹介していますので、合わせてご覧ください。
このように、制御器を設計する際は、それがプロパーであるのか、プロパーでないなら「厳密でない手段」で代替可能であるのか、を考慮する必要があります。
以上、プロパーなシステムの意味とイメージについての説明でした。制御工学でよく出てくる概念ですので、しっかり抑えておきましょう!
- 伝達関数が「分子の次数≦分母の次数」を満たすシステムを「プロパーなシステム」と呼ぶ
- プロパーなシステムは、現実世界で厳密な実現が可能である
- プロパーでないシステムは、現実世界で厳密な実現が不可能である
- ただし、システムがプロパーでなくても「ほぼ等しいシステム」で代替できることが多い




コメント