このページでは伝達関数の基本となる1次遅れ要素・2次遅れ要素・積分要素・比例要素と、それぞれの具体例について解説します。
※伝達関数の基本を未学習の方は、まずこちらの記事をご覧ください。
- 伝達関数の基本は、1次遅れ要素・2次遅れ要素・積分要素・比例要素
- 上記要素を理解していれば、より複雑なシステムもこれらの組み合わせで対応できる!
1次遅れ要素
1次遅れ要素とは
入出力関係が、次のような1階の線形微分方程式で表現されるものを、1次遅れ要素と呼びます。
$$a_1 \dot{y}(t) + a_0 y(t) = b_0 u(t)$$
ラプラス変換すると、次のようになりますね。
$$ Y(s) = \ubg{\frac{b_0}{a_1 s + a_0}}{伝達関数G(s)} U(s)$$
微分が1階なので、伝達関数の分母の$s$の次数が1になっているのがポイントです。1次遅れ要素単体で構成されるシステムは、1次系・1次遅れ系・1次システムなどと呼ばれます。
※1次系の詳しい特性については、こちらのページをご覧ください。
以下、1次系の例と伝達関数を紹介していきましょう。
例:並進運動系の伝達関数
まず、機械システムの例です。
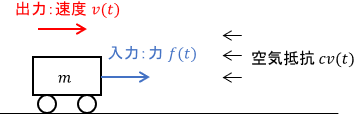

入力は台車に加わる力$f(t)$、出力は台車の速度$v(t)$、$m$は台車の質量、$c$は空気抵抗の係数です。この台車の運動方程式を求めると、次式が得られます。
$$m\dot{v}(t) = -cv(t) + f(t)$$
1階の微分方程式となっていますね。これをラプラス変換すると、次式となります。
$$msV(s) = -cV(s) + F(s)$$
出力についてまとめると、伝達関数が得られます。
$$V(s) = \ubg{\frac{1}{ms+c}}{伝達関数G(s)} F(s)$$
例:回転運動系の伝達関数
続いては、回転運動する機械システムです。
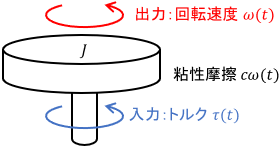

入力はトルク$\tau(t)$、出力は回転速度$\omega(t)$、$J$は円盤の慣性モーメント、$c$は粘性摩擦係数です。この円盤の運動方程式を求めると、次式が得られます。
$$J \dot{\omega}(t) = -c \omega(t) + \tau(t)$$
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather} J s\Omega(s) = -c \Omega(s) + T(s) \\[5pt] \Omega(s) = \ubg{\frac{1}{Js+c}}{伝達関数G(s)} T(s)\end{gather}$$
先ほどの例と本質的には同じ構成をしていますね。
機械システムは次に紹介する2次遅れ要素で表される場合がほとんどですが、上の2つの例のように「入力が力・出力が速度」でまとめられる場合は1次遅れ要素で表現できることは覚えておきましょう。
例:RC回路の伝達関数
電気システムの例としては、RC回路が挙げられます。
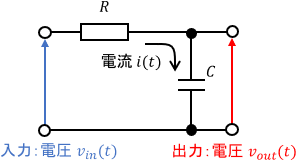

入力は電圧$v_{in}(t)$、出力は電圧$v_{out}(t)$、$i(t)$は回路を流れる電流、$R$は抵抗値、$C$はコンデンサの容量です。コンデンサに着目すると、電流$i(t)$は次式で求められます。
$$i(t) = C\dot{v}_{out}(t)$$
また、それぞれの要素に加わる電圧は次のように計算できます。
$$\begin{align} 抵抗両端の電圧&:Ri(t) \\[5pt] コンデンサ両端の電圧&:v_{out}(t)\end{align}$$
キルヒホッフの法則より、各電圧の関係が次のように表されます。
$$\begin{align} v_{in}(t) &= Ri(t) + v_{out}(t) \\[5pt] &= RC \dot{v}_{out}(t)+ v_{out}(t)\end{align}$$
あとはラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}V_{in}(s) = RCs V_{out}(s) + V_{out}(s) \\[5pt] V_{out}(s) = \ubg{\frac{1}{RCs + 1}}{伝達関数G(s)} V_{in}(s)\end{gather}$$
2次遅れ要素
2次遅れ要素とは
入出力関係が、次のような2階の線形微分方程式で表現されるものを、2次遅れ要素と呼びます。
$$a_2 \ddot{y}(t) + a_1 \dot{y}(t) + a_0 y(t) = b_0 u(t)$$
ラプラス変換すると、次のようになりますね。
$$ Y(s) = \ubg{\frac{b_0}{a_2 s^2 + a_1 s + a_0}}{伝達関数G(s)} U(s)$$
微分が2階なので、伝達関数の分母の$s$の次数が2になっているのがポイントです。2次遅れ要素単体で構成されるシステムは、2次系・2次遅れ系・2次システムなどと呼ばれます。
※2次系の詳しい特性については、こちらのページをご覧ください。
以下、2次系の例と伝達関数を紹介していきましょう。
例:ばねダンパ系の伝達関数
機械システムの例です。
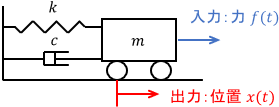

入力は台車に加わる力$f(t)$、出力は台車の位置$x(t)$、$m$は台車の質量、$k$はばね定数、$c$は粘性係数です。この台車の運動方程式を求めると、次式が得られます。
$$m\ddot{x}(t) = -c\dot{x}(t) – k x(t) + f(t)$$
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}m s^2 X(s) = -c s X(s) – k X(s) + F(s)\\[5pt] X(s) = \ubg{\frac{1}{ms^2 + c s + k}}{伝達関数G(s)} F(s)\end{gather}$$
ばねやダンパがない場合は、$k,c$をそれぞれ0に設定すればOKです。
例:振り子の伝達関数
回転運動する機械システムも、同様に2次系で表されます。
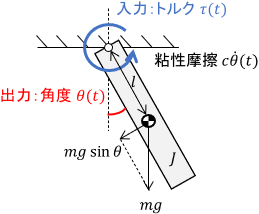

入力はトルク$\tau(t)$、出力は角度$\theta(t)$、$J$は回転軸まわりの振り子の慣性モーメント、$m$は振り子の質量、$c$は粘性摩擦係数、$g$は重力加速度です。$\theta=0$近傍の運動のみを考えるとし、$\sin \theta \approx \theta$と近似すると、振り子の運動方程式は次のようになります。
$$\begin{align} J \ddot{\theta}(t) &= -c \dot{\theta}(t) – mgl \sin \bigl( \theta(t) \bigr) + \tau(t) \\[3pt] & \approx -c \dot{\theta}(t) – mgl \theta(t) + \tau(t)\end{align}$$
※$\theta=0$まわりで、テイラー展開を用いた1次近似を行っています。テイラー展開については、こちらのページをご覧ください
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}J s^2 \Theta (s) = -c s \Theta (s) – mgl \Theta(s) + T(s) \\[5pt] \Theta (s) = \ubg{\frac{1}{Js^2 +c s + mgl}}{伝達関数G(s)} T(s) \end{gather}$$
なお、回転軸まわりの慣性モーメント$J$ではなく、重心まわりの慣性モーメント$J_G$が与えられている場合は、それを$J=J_G+ml^2$と回転軸まわりの慣性モーメントに変換し、上式を適用すればOKです。
また、次のように剛体でなく質点である振り子の場合は、上式の慣性モーメントを$J=ml^2$と設定したものが伝達関数となります。
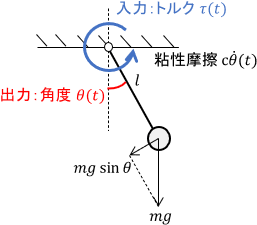

運動方程式は位置(or角度)に関する2階の微分方程式なので、上の2つの例のように「入力が力・出力が位置」である機械システムは基本的に2次系となります。
例:RLC回路の伝達関数
続いて、電気システムの例です。
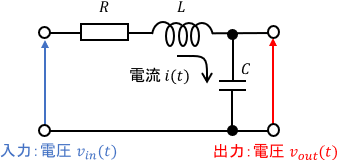

入力は電圧$v_{in}(t)$、出力は電圧$v_{out}(t)$、$i(t)$は回路を流れる電流、$R$は抵抗値、$L$はコイルのインダクタンス、$C$はコンデンサの容量です。RC回路の場合と同様にコンデンサに着目すると、電流$i(t)$は次式で求められます。
$$i(t) = C\dot{v}_{out}(t)$$
また、それぞれの要素に加わる電圧は次のように計算できます。
$$\begin{align} 抵抗両端の電圧&:Ri(t) \\[3pt] コイル両端の電圧&:L\dot{i}(t) \\[5pt] コンデンサ両端の電圧&:v_{out}(t)\end{align}$$
キルヒホッフの法則より、各電圧の関係が次のように表されます。
$$\begin{align} v_{in}(t) &= Ri(t) + L\dot{i}(t) + v_{out}(t) \\[5pt] &= RC \dot{v}_{out}(t) + LC\ddot{v}_{out}(t) + v_{out}(t)\end{align}$$
あとはラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}V_{in}(s) = LCs^2 V_{out}(s) + RCs V_{out}(s) + V_{out}(s) \\[5pt] V_{out}(s) = \ubg{\frac{1}{LCs^2 + RCs + 1}}{伝達関数G(s)} V_{in}(s) \end{gather}$$
積分要素
積分要素とは
入出力関係が、次のような1階の線形微分方程式で表現されるものを、積分要素と呼びます。
$$ \dot{y}(t) = b_0 u(t)$$
ラプラス変換すると、次のようになりますね。
$$ Y(s) = \ubg{\frac{b_0}{s}}{G(s)} U(s)$$
伝達関数に積分を表す$\frac{1}{s}$が単体で入っているのがポイントです。
微分方程式の解は、ラプラス変換するまでもなく入力の積分によって得られますね($y$の初期値は0としています)
$$ y(t) = {b_0} \int _0 ^t u(\tau) d\tau$$
よって、積分要素は「時々刻々、与えられた入力が蓄積していく様子を表す」とイメージすればOKです。
※積分要素の詳しい特性については、こちらのページをご覧ください
以下、積分要素で表されるシステムの例と伝達関数を紹介していきましょう。
例:並進運動系の伝達関数(抵抗なし)
まずは、機械システムの例です。
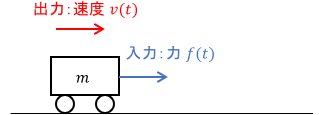

入力は台車に加わる力$f(t)$、出力は台車の速度$v(t)$、$m$は台車の質量です。1次系にて考えた例の空気抵抗がないケースですね。この台車の運動方程式を求めると、次式が得られます。
$$m\dot{v}(t) = f(t)$$
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}msV(s) = F(s) \\[5pt] V(s) = \ubg{\frac{1}{ms}}{G(s)} F(s) \end{gather}$$
与えた力が運動エネルギーとして時々刻々蓄積し、速度を形成する様子を表していると解釈できます。
例:水位系の伝達関数
続いて、下図のようにタンクに水が供給されるシステムを考えます。
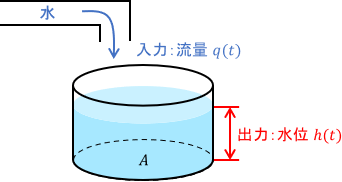

入力は流量$q(t)\mathrm{[m^3/s]}$、出力は水位$h(t)\mathrm{[m]}$、$A\mathrm{[m^2]}$はタンクの断面積です。タンク内の水の体積変化に着目すると、流量$q(t)$と水位$h(t)$の関係は次式で表されます。
$$A\dot{h}(t) = q(t)$$
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather} AsH(s) = Q(s) \\[5pt] H(s) = \ubg{\frac{1}{As}}{G(s)} Q(s) \end{gather}$$
与えた水が時々刻々蓄積し、水位を形成する様子を表していると解釈できます。
例:熱系の伝達関数
下図のように、タンク内の水をヒータで加熱するシステムを考えます。
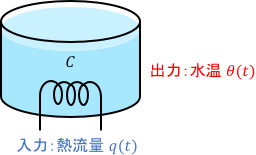

入力は熱流量$q(t)\mathrm{[J/s]}$、出力は水温$\theta(t)\mathrm{[^\circ C]}$、$C\mathrm{[J/^\circ C]}$は水の熱容量です。タンク内の水の温度変化に着目すると、熱流量$q(t)$と水温$\theta(t)$の関係は次式で表されます。
$$C\dot{\theta}(t) = q(t)$$
ラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}Cs\Theta(s) = Q(s) \\[5pt] \Theta(s) = \ubg{\frac{1}{Cs}}{G(s)} Q(s) \end{gather}$$
与えた熱が時々刻々蓄積し、温度を形成する様子を表していると解釈できます。
比例要素
比例要素とは
入出力関係が次式で表現されるものを、比例要素と呼びます。
$$ y(t) = K u(t)$$
ラプラス変換しても、そのまま比例関係が成り立ちます。
$$ Y(s) = \ubg{K}{G(s)} U(s)$$
これは微分方程式ではなくただの代数方程式なので、比例要素は静的システムです。
※動的システムと静的システムの詳細については、こちらの記事をご覧ください。
以下、比例要素で表されるシステムの例と伝達関数を紹介していきましょう。
例:ばねの伝達関数
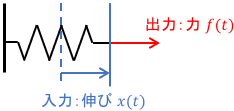

入力はばねの伸び$x(t)$、出力は力$f(t)$、$k$はばね定数です。これらの関係はフックの法則で表されます。
$$f(t) = kx(t)$$
ラプラス変換すると、ばね定数がそのまま伝達関数となります。
$$F(s) = \ubg{k}{G(s)}X(s)$$
例:抵抗の伝達関数
簡単な分圧回路を考えましょう。
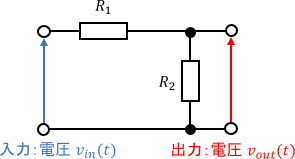

入力は電圧$v_{in}(t)$、出力は電圧$v_{out}(t)$、$R_1,R_2$は抵抗値です。合成抵抗の式とオームの法則から、これらの関係は次式で表されます。
$$v_{out}(t) = \frac{R_2}{R_1 + R_2} v_{in}(t)$$
ラプラス変換すると、合成抵抗値がそのまま伝達関数となります。
$$V_{out}(s) = \ubg{\frac{R_2}{R_1 + R_2}}{G(s)} V_{in}(s)$$
より複雑なシステム
ここまで、伝達関数の基本となる非常にシンプルなシステムを紹介してきました。これ以上複雑なシステム(微分方程式が3階以上となるシステム)は高次系(高次システム)と呼ばれます。
高次系はたしかに複雑ですが、その伝達関数のほとんどは1次遅れ要素・2次遅れ要素・積分要素・比例要素の組み合わせで表現できることが知られています。
よって、ここで紹介した各要素を理解していれば、その考え方を高次系にもそのまま拡張することができます。基本システムを制するものは高次系も制す、というわけですね!
※高次系の詳細はこちらのページで解説していますので、合わせてご覧ください。
以上、伝達関数の基本要素とその具体例でした!
- 伝達関数の基本は、1次遅れ要素・2次遅れ要素・積分要素・比例要素
- 上記要素を理解していれば、より複雑なシステムもこれらの組み合わせで対応できる!










コメント