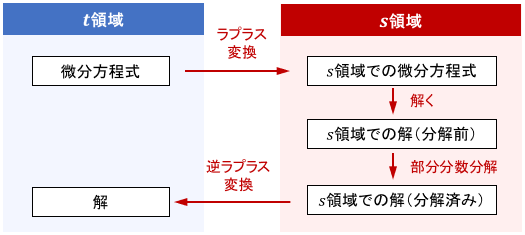
このページでは、ラプラス変換を用いた微分方程式の解き方について、手順・よくあるパターン・例題を交えて解説します。
- 微分方程式全体をラプラス変換し、$s$領域で解を求めた後、それを逆ラプラス変換すれば解ける
- 使用する逆ラプラス変換にはある程度パターンがあるので、それを抑えておけば便利
- 途中で必要となる部分分数分解も、上記パターンを目指しながら行えばOK
ラプラス変換による微分方程式の解き方
ラプラス変換表
まずは、公式として覚えておくべき代表的なラプラス変換を復習しておきましょう。
※ラプラス変換の基礎や下記公式について未学習の方は、まずこちらのページをご覧ください。
基本性質表
| $t$領域 | $s$領域 | メモ |
|---|---|---|
| $af(t)+bg(t)$ | $aF(s)+bG(s)$ | 線形性 |
| $\dot{f}(t)$ | $sF(s)-f(0)$ | 微分 |
| $\int_0 ^t f(\tau)d\tau$ | $\frac{1}{s}F(s)$ | 積分 |
| $e^{at}f(t)$ | $F(s-a)$ | 移動定理 |
基本変換表
| $t$領域 | $s$領域 | 覚え方 | |
|---|---|---|---|
| ① | $t^n$ | $\frac{n!}{s^{n+1}}$ | これがベース |
| ② | $1$ | $\frac{1}{s}$ | ①の$n=0$ |
| ③ | $t$ | $\frac{1}{s^2}$ | ①の$n=1$ |
| ④ | $t^2$ | $\frac{2}{s^3}$ | ①の$n=2$ |
| ⑤ | $e^{at}$ | $\frac{1}{s-a}$ | ②+移動定理 |
| ⑥ | $t^n e^{at}$ | $\frac{n!}{(s-a)^{n+1}}$ | ①+移動定理 |
| $t$領域 | $s$領域 | 覚え方 | |
|---|---|---|---|
| ① | $\sin\omega t$ | $\frac{\omega}{s^2+\omega ^2}$ | これがベース |
| ② | $\cos\omega t$ | $ \frac{s}{s^2+\omega ^2}$ | これもベース |
| ③ | $e^{at}\sin\omega t$ | $\frac{\omega}{(s-a)^2+\omega ^2}$ | ①+移動定理 |
| ④ | $e^{at}\cos\omega t$ | $\frac{s-a}{(s-a)^2+\omega ^2}$ | ②+移動定理 |
微分方程式を解く手順
上記を用いて微分方程式を解く手順は、次のようにまとめられます。
- まず微分方程式全体をラプラス変換し、問題を$s$領域に移す
- 数式を整理し、$s$領域での解を導出する
- 得られた解を部分分数分解し、各項の分母がこれ以上因数分解できない形にしておく
- 各項を逆ラプラス変換することで、$t$領域での解を得る

逆ラプラス変換パターンまとめ
上記手順の最後にある逆ラプラス変換では、現れる数式パターンがある程度決まっているので、それらを抑えておくと問題が解きやすくなります。順番に紹介していきましょう。
基本形
まずは、分母が$s+\alpha$($\alpha$は定数)の形をしている場合です。公式に当てはめるだけの基本パターンですね。
$$\begin{align}\color{green}{使う公式:}&\ \ \color{green}{\frac{1}{s-a} \ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{at}}\\[7pt] 例:&\ \ \frac{1}{s+3}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{-3t}\end{align}$$
「2乗+定数」の形
分母が$s^2+\alpha$の形をしている場合は、三角関数への変換を目指します。
$$\color{green}{使う公式:\ \ \frac{\omega}{s^2+\omega ^2}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ \sin\omega t,\quad \ \frac{s}{s^2+\omega ^2}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ \cos\omega t}$$
$$\begin{align}例1:\ \ & \frac{6}{s^2+4}=3\cdot \frac{2}{s^2+4}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ 3 \sin 2t \\[7pt] 例2: \ \ & \frac{2s}{s^2+4} = 2 \cdot \frac{s}{s^2+4}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ 2 \cos 2t \end{align}$$
次のように分子が複数の項を持つ場合は一瞬戸惑いますが、各項ごとの足し算に分解すればOKです。
$$例:\ \ \frac{2s+6}{s^2+4} = \frac{2s}{s^2+4} + \frac{6}{s^2+4}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ 2\cos 2t + 3\sin 2t$$
「2乗-定数」の形
分母が$s^2-\alpha$の形をしている場合は、さらに部分分数分解できるので、地道に計算を進めましょう。
$$\color{green}{使う公式:\ \ \frac{1}{s-a} \ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{at}}$$
$$例:\ \ \frac{16}{s^2-16} = \frac{16}{(s+4)(s-4)} = 2 \bigg( \frac{1}{s-4}-\frac{1}{s+4} \bigg) \ \xrightarrow{\ \mathcal{L}^{-1}\ }\ 2e^{4t} – 2e^{-4t}$$
「2乗+1乗+定数」の形
分母が$s^2+\alpha s+\beta$の形をしている場合は、分母を平方完成して$e^{-at}\sin \omega t$や$e^{-at}\cos \omega t$への変換を目指します。
$$\color{green}{使う公式:\ \ \frac{\omega}{(s-a)^2+\omega ^2} \ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{at}\sin\omega t,\quad \ \frac{s-a}{(s-a)^2+\omega ^2}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{at}\cos\omega t}$$
$$\begin{align}例1:& \ \ \frac{2}{s^2+2s+3}=\sqrt{2}\cdot \frac{\sqrt{2}}{(s+1)^2+2}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ \sqrt{2}e^{-t} \sin \sqrt{2}t \\[7pt]例2: & \ \ \frac{s+1}{s^2+2s+3} = \frac{s+1}{(s+1)^2+2}\ \xrightarrow{\ \mathcal{L}^{-1}\ }\ e^{-t} \cos \sqrt{2}t \end{align}$$
よく出てくるパターンは以上です。
また、逆ラプラス変換の前には$s$領域で求めた解を部分分数分解する工程がありますが、そのときには上記の形を目指せばすんなりと解けるでしょう。
※部分分数分解の方法については、こちらのページで詳しく解説していますので、合わせてご覧ください
1階の微分方程式の例
それでは、上記を使いながら、具体的に微分方程式を解いていきましょう。
※以降では数式を見やすくするために、混乱のない範囲で、時間の関数$x(t)$を$x$、$x(t)$のラプラス変換$X(s)$を$X$と簡略化して表記します。
シンプルな例
まずは、こちらの問題を考えましょう。
$$2\dot{x}+3x=0\quad ただし\quad x(0)=1$$
解き方の手順に沿って、解を求めていけばOKです。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &2\big\{ sX – x(0) \big\} +3X=0\\[12pt] \color{green}{x(0)を代入}\quad &2sX – 2 +3X=0\\[10pt] \color{green}{Xで整理}\quad & \big(2s+3\big)X = 2\\[5pt] &X = \frac{2}{2s+3}=\frac{1}{s+\frac{3}{2}}\\[5pt] \color{green}{逆ラプラス変換}\quad& x(t)=e^{-\frac{3}{2}t}\end{align}$$
部分分数分解が必要な例
続いてはこちらです。
$$\dot{x}+5x=1\quad ただし\quad x(0)=2$$
まずは、$s$領域での解を求めていきましょう。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad & \big\{ sX-x(0)\big\}+5X=\frac{1}{s}\\[7pt] \color{green}{x(0)を代入}\quad &sX-2+5X=\frac{1}{s} \\[7pt] \color{green}{Xで整理}\quad &\big( s + 5 \big)X = \frac{1}{s} + 2 \\[7pt] & X =\color{blue}{\frac{1}{s(s+5)}}+\frac{2}{s+5}\end{align}$$
このままでは解を逆ラプラス変換できないので、青の部分を部分分数分解しましょう。
※以降では、「部分分数分解のお手軽裏ワザ」と称して本サイトで勝手にオススメしている、分子展開法を使って分解していきます。分子展開法は、「分子を分母因数の足し引きの形に展開することで、部分分数分解を行う方法」です。詳しくは、こちらのページをご覧ください
$$\begin{align} X &= \color{blue}{\frac{1}{5}\cdot \frac{(s+5)-s}{s(s+5)}} + \frac{2}{s+5}\\[5pt] &= \color{blue}{\frac{1}{5}\bigg( \frac{1}{s}\ -\ \frac{1}{s+5}\bigg) }+ \frac{2}{s+5}\ =\ \frac{1}{5}\cdot\frac{1}{s}\ +\ \frac{9}{5}\cdot\frac{1}{s+5}\end{align}$$
分解できたので、後はそれぞれの項を逆ラプラス変換すれば、解が求まります。
$$x(t)=\frac{1}{5}\ +\ \frac{9}{5}e^{-5t}$$
三角関数が現れる例
続いて、こちらの問題を解いてみましょう。
$$\dot{x}+2x=\sin t\quad ただし\quad x(0)=0$$
これまでと同様に、$s$領域での解を求めていきます。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad & \big\{ sX-x(0) \big\}+2X=\frac{1}{s^2+1}\\[7pt] \color{green}{x(0)を代入してXで整理}\quad & X=\frac{1}{(s+2)(s^2+1)}\end{align}$$
分母に積の形が現れたので、部分分数分解しましょう。分子を、分母の因数を含んだ形に変形します。
$$\begin{alignat}{2} X&\ =\frac{1}{5}\cdot \frac{(s^2+1)-(s+2)(s-2)}{(s+2)(s^2+1)}& &=\ \frac{1}{5} \bigg( \frac{1}{s+2}\ -\ \frac{s-2}{s^2+1} \bigg) \\[5pt] &=\ \frac{1}{5}\bigg( \frac{1}{s+2}\ -\ \frac{s}{s^2+1} + 2\cdot \frac{1}{s^2+1}\bigg)& &\end{alignat}$$
後は、これを逆ラプラス変換すればOKですね。
$$x(t)=\frac{1}{5} \big(e^{-2t} – \cos t + 2\sin t \big)$$
2階の微分方程式の例
部分分数分解が必要な例
続いては、方程式に2階微分が含まれる場合です。とはいっても、解き方はこれまでと全く同じです。
$$\ddot{x}-3\dot{x}+2x=0 \quad ただし\quad x(0)=0,\ \dot{x}(0)=-1$$
これまで通り、$s$領域での解を求めていきます。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &\big\{ s^2 X – sx(0) – \dot{x}(0) \big\} -3\big\{ sX-x(0) \big\} + 2X=0\\[10pt] \color{green}{x(0),\dot{x}(0)を代入}\quad & s^2X+1-3sX + 2X=0\\[10pt] \color{green}{Xで整理}\quad & \big( s^2 -3s+2\big)X = -1 \\[7pt] &X\ =\ \frac{-1}{s^2-3s+2}\ =\ \frac{-1}{(s-1)(s-2)}\end{align}$$
例のごとく、部分分数分解しましょう。
$$X\ =\ \frac{(s-2)-(s-1)}{(s-1)(s-2)}\ =\ \frac{1}{s-1}\ -\ \frac{1}{s-2}$$
後は逆ラプラス変換するだけです。
$$x(t)=e^t – e^{2t}$$
三角関数が現れる例
続いてはこちらです。
$$\ddot{x}-{x}=-10\sin 2t \quad ただし\quad x(0)=-1,\ \dot{x}(0)=0$$
$s$領域での解を求めていきます。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &\big\{ s^2 X – sx(0) – \dot{x}(0) \big\} – X =-10\cdot \frac{2}{s^2+4}\\[10pt] \color{green}{x(0),\dot{x}(0)を代入}\quad & s^2X+s-X=-\ \frac{20}{s^2+4}\\[7pt] \color{green}{Xで整理}\quad & \big( s^2-1\big)X = -\ \frac{20}{s^2+4}-s\\[7pt] &X =-\ \color{blue}{\frac{20}{(s^2+4)(s^2-1)}}- \color{black}{\frac{s}{s^2-1}}\end{align}$$
青の部分を、部分分数分解していきましょう。
$$\begin{alignat}{2} X &=\color{blue}{-\ 4\cdot \frac{(s^2+4)-(s^2-1)}{(s^2+4)(s^2-1)}}- \color{black}{\frac{s}{s^2-1}} & &\ =\color{blue}{\ – 4\bigg\{ \frac{1}{s^2-1}\ -\ \frac{1}{s^2+4}\bigg\}} – \frac{s}{s^2-1} \\[5pt] & =\color{green}{ -\ \frac{4}{s^2-1}\ -\ \frac{s}{s^2-1}} + \frac{4}{s^2+4}& &\end{alignat}$$
前述のパターンの通り、緑の部分はさらに分解が可能です。ちょっと面倒ですが、地道に分解していきましょう。
$$\begin{align} X &=\color{green}{-\ 2\cdot \frac{(s+1)-(s-1)}{(s-1)(s+1)}\ -\ \frac{1}{2}\cdot\frac{(s+1)+(s-1)}{(s-1)(s+1)}} + \frac{4}{s^2+4}\\[5pt] &= \color{green}{ -2 \bigg\{ \frac{1}{s-1}\ -\ \frac{1}{s+1} \bigg\}\ -\ \frac{1}{2} \bigg\{ \frac{1}{s-1} + \frac{1}{s+1} \bigg\} } + \frac{4}{s^2+4} \\[5pt] &= -\frac{5}{2}\cdot\frac{1}{s-1}\ +\ \frac{3}{2}\cdot\frac{1}{s+1}\ +\ 2\cdot \frac{2}{s^2+4}\end{align}$$
分解できたので、逆ラプラス変換して、$t$領域での解を求めましょう。
$$x(t)=-\frac{5}{2}e^t + \frac{3}{2} e^{-t} + 2\sin 2t$$
平方完成が必要な例
続いて、こちらの問題を考えましょう。
$$\ddot{x}+2\dot{x}+3x=3 \quad ただし\quad x(0)=0,\ \dot{x}(0)=1$$
例のごとく、$s$領域での解を求めていきます。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &\big\{ s^2 X – sx(0) – \dot{x}(0) \big\} +2\big\{ sX-x(0) \big\} + 3X=\frac{3}{s}\\[10pt] \color{green}{x(0),\dot{x}(0)を代入}\quad & s^2X -1 + 2sX + 3X = \frac{3}{s}\\[10pt] \color{green}{Xで整理}\quad & \big( s^2 +2s+3\big)X = \frac{3}{s}+1 \\[7pt] &X = \color{blue}{\frac{3}{s(s^2+2s+3)}}+\frac{1}{s^2 + 2s + 3}\end{align}$$
青の部分を、部分分数分解します。
$$\begin{align} X &= \color{blue}{ \frac{(s^2+2s+3)-s(s+2)}{s(s^2+2s+3)} } +\frac{1}{s^2 + 2s + 3} \\[5pt] & = \color{blue}{\frac{1}{s}\ -\ \frac{s+2}{s^2 + 2s + 3}} + \frac{1}{s^2 + 2s +3} \\[5pt] &= \frac{1}{s}\ -\ \frac{s+1}{s^2+2s+3}\end{align}$$
分母が2次式のパターンなので、平方完成しましょう。
$$X = \frac{1}{s}\ -\ \frac{s+1}{(s+1)^2+2}$$
あとは逆ラプラス変換するだけです。
$$\quad x(t) = 1 – e^{-t}\cos \sqrt{2} t$$
連立微分方程式の例
シンプルな例
最後に、次のように微分方程式が連立している場合についても見ていきましょう。これも、考え方はこれまでと全く同じです。
$$\left\{ \begin{array}{l} \dot{x} = 2x – 3y \\ \dot{y} = y -2x\end{array}\right. \quad ただし\quad x(0)=8,\ y(0)=3$$
解くべき変数が$x$と$y$の2つになっているので、まずはそれぞれの$s$領域での解を求めていきましょう。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &\left\{ \begin{array}{l} sX-x(0) = 2X – 3Y \\ sY-y(0) = Y -2X\end{array}\right.\\[7pt] \color{green}{x(0),y(0)代入}\quad &\left\{ \begin{array}{l} sX-8 = 2X – 3Y \\ sY-3 = Y -2X\end{array}\right.\\[7pt] \color{green}{X,Yで整理}\quad & \left\{ \begin{array}{l} (s-2)X + 3Y = 8 \\ 2X + (s-1)Y=3 \end{array}\right.\\[7pt] \color{green}{X,Yについて解く}\quad & X=\frac{8s-17}{(s+1)(s-4)},\quad Y=\frac{3s-22}{(s+1)(s-4)}\end{align}$$
$X$を部分分数分解し、$t$領域での解を求めます。
$$\begin{gather}X\ =\ \frac{3(s+1) + 5(s-4)}{(s+1)(s-4)}\ =\ \frac{3}{s-4} + \frac{5}{s+1}\\[7pt]逆ラプラス変換して、\quad x(t) = 3e^{4t} + 5e^{-t}\end{gather}$$
$y$も同様に求められますが、部分分数分解が面倒なら$t$領域での関係式を用いて直接求めてもOKです。具体的には、微分方程式で定義されている $\dot{x} = 2x – 3y$ の関係性を使って、次のように導出可能です。
$$\begin{align} y(t) &= \frac{1}{3}\big(2x-\dot{x}\big) \\[7pt] &= \frac{1}{3} \bigg\{ 2\big( 3e^{4t} + 5e^{-t} \big) – \big( 12e^{4t} – 5e^{-t}\big)\bigg\} \\[7pt] &=\frac{1}{3}\big( -6e^{4t} + 15e^{-t}\big) \\[7pt]&= -2e^{4t} + 5e^{-t}\end{align}$$
ちなみに、この方法を使う場合は$s$領域での解$Y$を求めることも不要です。
複雑な例
ちょっと複雑な例も見てみましょう。
$$\left\{ \begin{array}{l}4\dot{x} + 8x +\dot{y}=8\\ \dot{x} – y =10 \end{array}\right. \quad ただし\quad x(0)=0,\ y(0)=0$$
$s$領域での解を求めていきます。$x$も$y$も初期値は0なので、ラプラス変換は簡単ですね。
$$\begin{align}\color{green}{両辺ラプラス変換}\quad &\left\{ \begin{array}{l} 4sX + 8X + sY = \frac{8}{s} \\ sX-Y = \frac{10}{s} \end{array}\right.\\[7pt] \color{green}{X,Yについて解く}\quad & X=\color{blue}{\frac{8}{s(s^2+4s+8)}} + \frac{10}{s^2+4s+8}\\[7pt] &Y=\frac{8}{s^2+4s+8} + \frac{10s}{s^2+4s+8}\ -\ \frac{10}{s}\end{align}$$
$X$を逆ラプラス変換するために、青の部分を部分分数分解します。
$$\begin{alignat}{2} X &= \color{blue}{\frac{(s^2+4s+8)-s(s+4)}{s(s^2+4s+8)}} + \frac{10}{s^2+4s+8} & &\\[7pt] &= \color{blue}{\bigg\{ \frac{1}{s}\ -\ \frac{s+4}{s^2+4s+8}\bigg\}} + \frac{10}{s^2+4s+8} & &= \frac{1}{s}\ \color{green}{-\ \frac{s-6}{s^2+4s+8}}\end{alignat}$$
あとは緑の部分を平方完成すれば、逆ラプラス変換可能となります。
$$\begin{align} X &= \frac{1}{s} \ \color{green}{- \ \frac{(s+2)-8}{(s+2)^2+4}}\\[7pt] &= \frac{1}{s}\ \color{green}{-\ \frac{s+2}{(s+2)^2+4} + 4\cdot \frac{2}{(s+2)^2+4}}\end{align}$$
$$逆ラプラス変換して、\quad x(t) = 1 – e^{-2t} \cos 2t + 4e^{-2t}\sin 2t $$
$Y$も部分分数分解するのは面倒なので、元の関係式である $\dot{x} – y =10$ を使って$y$を導出しましょう。
$$y(t)\ =\ \dot{x} – 10\ =\ -6 e^{-2t} \sin 2t + 10 e^{-2t}\cos 2t – 10$$
以上、ラプラス変換を用いた微分方程式の解き方についての解説でした。
- 微分方程式全体をラプラス変換し、$s$領域で解を求めた後、それを逆ラプラス変換すれば解ける
- 使用する逆ラプラス変換にはある程度パターンがあるので、それを抑えておけば便利
- 途中で必要となる部分分数分解も、上記パターンを目指しながら行えばOK






コメント