インパルス入力に対するシステムの応答のことを、インパルス応答と呼びます。インパルス応答はシステムの特性を分析するのに非常に有用ですが、最初はイメージが付きにくいかもしれません。
このページでは、インパルス応答のイメージ・求め方・使い方を具体例を通じて解説します。
- インパルス応答は「最初に一瞬ガンッ!と大きな入力(インパルス入力)を与え、あとは何もせずほっといたらどうなるか」を表したもの
- インパルス入力はラプラス変換すると1になるため、非常に扱いやすいのが利点
- 完璧なインパルス入力は現実に実現不可能なので、実用上は「インパルス入力っぽい入力」を与えて「ちょっと誤差はあるけどインパルス応答っぽい出力」を得る
インパルス入力と単位インパルス関数
まず、インパルス応答を作り出すインパルス入力について詳しく見ていきましょう。
インパルス入力は、数学的には単位インパルス関数(またはDiracのデルタ関数)と呼ばれる関数$\delta(t)$で表現されます。これは少し特殊な関数で、次の性質を持っています。
$$\begin{gather} \int ^\infty _{-\infty} \delta(t) dt = 1 \\[3pt] \delta(t)=0 \ (t \neq 0) \end{gather}$$
1つ目の式は「積分すると面積が1になる」という性質を、2つ目の式は「$t=0$以外では値が$0$である」という性質を表しているわけですが、ちょっとイメージがつきにくいですね…
もう少し直感的に説明しましょう。下図のような長方形の関数を、面積1を保ったまま0近傍にギューッ!と圧縮するとします。
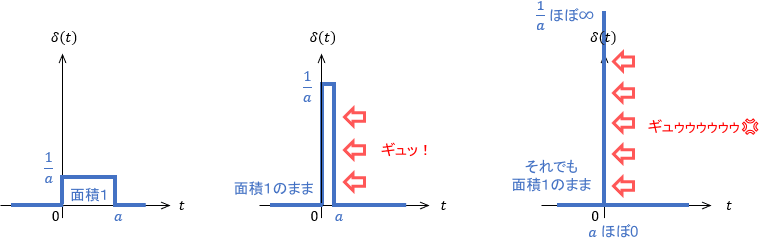

このとき、長方形のカド$a$に対し$a \rightarrow 0$と極限をとったもの、つまり長方形を極限まで圧縮したものが単位インパルス関数となります。
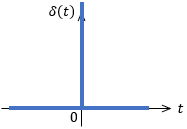
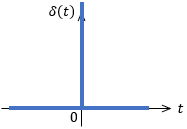
よって、簡単にいうと次式のようなイメージを持てばOKです。
$$\delta (t) = \left\{ \begin{array}{ll} \infty &(t=0)\\ 0 &(t \neq 0) \end{array} \right.$$
ただ、この表現だと数学的に厳密に考えたときにいろいろ不都合が生じるので、厳密な表現としては上で示したややこしい式が使われます。
「不都合が生じる」という部分のイメージもざっくりと説明しておきましょう。そもそも、システムに無限大の入力を与えるってかなりヤバそうですよね。普通に考えて、一瞬でも無限大の入力が加わればシステムは発散してしまいます。そこに「積分すると1」という条件を設けることで「入力信号は実質無限大だけど、物理的に無限のエネルギーを加えているわけではない」ということになり、システムの発散をいい感じに防げているというわけです。
インパルス応答のイメージ
このインパルス入力をシステムに与えたときの応答がインパルス応答となるわけですが、これはどのようにイメージすればよいでしょうか?
制御では$t=0$から動作が開始されると考えるので、「最初に一瞬ガンッ!と大きな入力を与え、あとは何もせずほっといたらどうなるか」を表しているといえます。
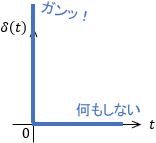

インパルスは「衝撃」という意味ですので、名前そのままのイメージですね。
最初以外の入力は全部0なので、インパルス応答は「何もせずほっといたらどうなるか」に着目したものだとも解釈できます。ただ、例えば最初から止まっているシステムをほっといても止まったままなので、最初に一瞬ガンッと入力を与えて平衡状態を乱しているわけですね。
インパルス応答の具体例
それでは、インパルス応答の具体例を見ていきましょう。数学的な詳細は別ページで解説しますので、ここでは大まかなイメージが把握できればOKです。
機械システム
まず機械システムの例です。次のようなばねダンパ系を考えましょう。
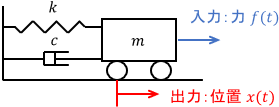

入力は力$f(t)$、出力は台車の位置$x(t)$です。よって、力$f(t)$をインパルス状に与えるとこのシステムのインパルス応答が得られます。


簡単に言うと、台車をハンマーでガンッ!とぶっ叩いたときの挙動ですね。
電気システム
続いて、電気システムの例です。次のようなRC回路を考えます。
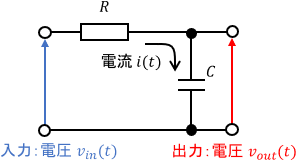

入力・出力はそれぞれ電圧$v_{in}(t),v_{out}(t)$です。よって、電圧$v_{in}(t)$をインパルス状に与えるとこのシステムのインパルス応答が得られます。


こちらも簡単に言うと、入力側のスイッチを一瞬だけピッ!と入れたときの挙動ですね。
フィードバック制御システム
最後にフィードバック制御システムの例です。先ほどのばねダンパ系を制御する、次のようなシステムを考えましょう。


入力は位置の目標値$r(t)$、出力は台車の位置$x(t)$です。よって、目標値を一瞬だけ変な値に設定し、あとは0目指して制御させたときの挙動を表していると解釈できます。
以上のように、入出力をどう設定するかによって入力や応答の物理的意味が変わるので注意してください。インパルス応答に限った話ではありませんが、システムの応答を見る上で重要なのは「自分が今どの信号の関係性を見ているのか」をしっかりと把握することですので、これを常に意識しておきましょう。
※ちなみに上のようなフィードバック制御システムでは、「どの信号の関係性を見ているのか」に応じて伝達関数の呼び方を変えることがあります。詳しくはこちらの記事をご覧ください。
インパルス応答の利点
インパルス入力(すなわち単位インパルス関数$\delta(t)$)は、ラプラス変換すると1になるため非常に扱いやすいのが最大の特徴です。
$$\delta(t)\ \xrightarrow{\large ラプラス変換}\ 1$$
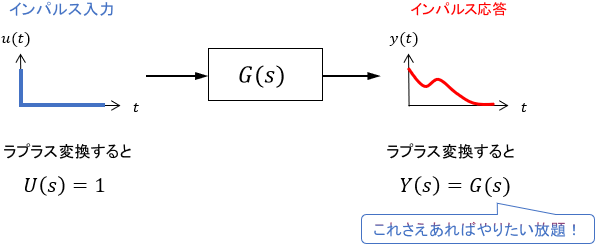
よって伝達関数$G(s)$で表されるシステムにインパルス入力$U(s)=1$を与えた場合、その出力$Y(s)$は伝達関数に等しくなります。
$$Y(s) = G(s)U(s) = G(s) \quad \color{green}{伝達関数そのまま!}$$
つまり、インパルス応答にはそのシステムのすべての情報が含まれていると言えます。
極端な話、システムの動作を分析する際、インパルス応答のデータさえあれば他のデータは全く必要ありません。インパルス応答$y(t)$をラプラス変換すると伝達関数$G(s)$が得られますから、それを用いればどんな動作も計算で再現できるというわけです。

※この性質を持つことから、インパルス応答は周波数解析にて重要な役割を担っています。インパルス応答と周波数特性の関係については、こちらのページをご覧ください。
インパルス入力の実際と使い方
…とはいえ現実はそこまで甘くありません。理論的には上記のとおりなのですが、現実には完璧なインパルス入力を与える(無限大の入力を無限に短い時間だけ与える)なんて不可能ですよね。
よって、実際のところは「インパルス入力っぽい入力」を与えて「ちょっと誤差はあるけどインパルス応答っぽい出力」を得ることになります。「インパルス入力っぽい入力」は、「システムの平衡状態を乱せる大きさの入力を、できる限り小さな時間だけ与えたもの」とイメージすればOKです。
機械システムの例でいうと、ハンマーでシステムを一瞬だけカツーンと叩くイメージですね。こう書くと簡単そうですが、大きな力を文字通り一瞬だけ与えるよう叩くというのは意外と難しいものです。
世の中の工場や研究現場には、これがやたら上手いおじさんがいたりいなかったりします。


ちなみにインパルス入力を与えるとき、


よーし、本物のインパルス入力に近くなるようになるべく無限大に近い入力を与えるぞ!
と考えてはいけません。普通にシステムがぶっ壊れます。
現実には「入力を無限に短い時間だけ与える」ということができないため、数式でいう「積分したら1」という条件が満たされず、先ほど説明したようにいい感じに発散を防げないためです。
以上のようにインパルス入力は数式上は非常に扱いやすいのですが、現実世界での扱いには少し工夫が必要となります。よってシステムの特性分析の第一歩目としては、より扱いやすいステップ応答のほうがよく用いられます。
※ステップ応答の詳細については、こちらの記事をご覧ください。ちなみにステップ応答が扱いやすすぎるだけで、インパルス応答が扱いにくいというわけではありません。インパルス応答も全体の中ではかなり扱いやすい部類で、非常に多く用いられます。
以上、インパルス応答のイメージ・求め方・使い方でした。
- インパルス応答は「最初に一瞬ガンッ!と大きな入力(インパルス入力)を与え、あとは何もせずほっといたらどうなるか」を表したもの
- インパルス入力はラプラス変換すると1になるため、非常に扱いやすいのが利点
- 完璧なインパルス入力は現実に実現不可能なので、実用上は「インパルス入力っぽい入力」を与えて「ちょっと誤差はあるけどインパルス応答っぽい出力」を得る






コメント