このページでは、1次系(1次遅れ系・1次システム)のインパルス応答・ステップ応答の詳細を、具体例を交えて解説します。また、1次系のよくある使い方についても解説します。
※インパルス応答・ステップ応答の詳細については、こちらの記事をご覧ください。
- 1次系の伝達関数は、$G(s)=\frac{K}{Ts+1}$で表される。
- $K$はゲインと呼ばれる、出力の大きさを決めるパラメータ
- $T$は時定数と呼ばれる、出力の応答速度(収束時間)を決めるパラメータ
- 1次系は、信号の遅れをお手軽に表現するのに便利
1次系の数式モデル
入力$u(t)$と出力$y(t)$の関係が次のような1階の線形微分方程式で表現されるシステムを、1次系(1次遅れ系・1次システム)と呼びます。
$$a_1 \dot{y}(t) + a_0 y(t) = b_0 u(t)$$
ラプラス変換すると、次のようになりますね。
$$ Y(s) = \ubg{\frac{b_0}{a_1 s + a_0}}{伝達関数G(s)} U(s)$$
微分が1回なので、伝達関数の分母の$s$の次数が1になっているのがポイントです。
安定な1次系に対しては、各係数の意味を分かりやすくするために、伝達関数$G(s)$を次の形式で表記することがほとんどです。
$$ \begin{gather}G(s) = \frac{K}{T s + 1} \\[7pt] ただし、K=\frac{b_0}{a_0}, \quad T=\frac{a_1}{a_0}>0\end{gather}$$
$K$はゲイン、$T$は時定数と呼ばれる定数です。1次系の特性は、この2つの定数によって決定づけられます(これしかパラメータがないので当然ですが)。
ゲイン$K$はただの係数なので、1次系の本質部分は$\frac{1}{T s + 1}$で、その出力の大きさを$K$が決定しているとも解釈できます。
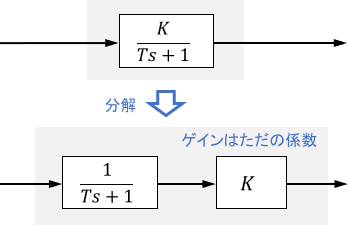

これを念頭に置きながら、ゲイン$K$・時定数$T$が、システムのインパルス応答・ステップ応答に及ぼす影響を具体的に見ていきましょう。
1次系のインパルス応答


まずはインパルス応答です。システムにインパルス入力$U(s)=1$を与え、インパルス応答$Y(s)$を求めましょう。
$$Y(s)=G(s)U(s)=\frac{K}{Ts+1}$$
当然、伝達関数そのものが出てきますね。これを逆ラプラス変換して、$t$領域での挙動を調べてみましょう。ちょっと式変形して逆ラプラス変換の公式に当てはめると、次式が得られます。
$$Y(s) = \frac{\frac{K}{T}}{s+\frac{1}{T}}\quad \xrightarrow{\large 逆ラプラス変換}\quad y(t)=\frac{K}{T} e^{-\frac{1}{T}t}$$
システムの極が$-\frac{1}{T}$なので、それがそのまま$e$の右肩に現れていますね。
※ラプラス変換の各種公式、および極と応答の関係性については、こちらのページをご覧ください
このインパルス応答をプロットすると、次のようになります。
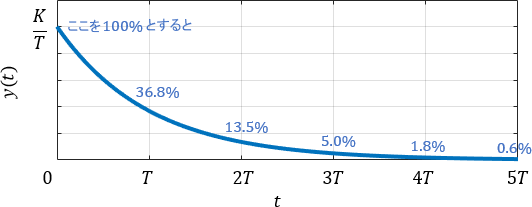

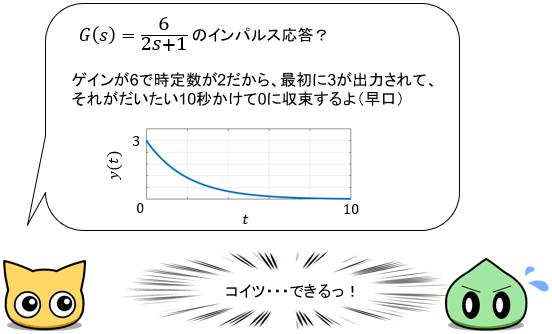
まず$\frac{K}{T}$が出力され、それがだいたい$5T$かけて$0$に収束していることが分かりますね。これを知っていれば、伝達関数を見ただけでインパルス応答の挙動が瞬時に分かるようになります!

余裕があれば、時刻$T$にて出力が36.8%(だいたい1/3)まで減衰することも覚えておきましょう。
1次系のステップ応答


続いてステップ応答を見ていきましょう。システムにステップ入力$U(s)=\frac{1}{s}$を与え、ステップ応答$Y(s)$を求めます。
$$Y(s)=G(s)U(s)=\frac{K}{Ts+1}\cdot \frac{1}{s}$$
これを逆ラプラス変換して、$t$領域での挙動を調べてみましょう。部分分数分解して逆ラプラス変換の公式に当てはめると、次式が得られます。
$$Y(s) = K \biggl( \frac{1}{s} – \frac{1}{s+\frac{1}{T}}\biggr) \quad \xrightarrow{\large 逆ラプラス変換}\quad y(t)=K\Bigl( 1 – e^{-\frac{1}{T}t} \Bigr)$$
これもシステムの極$-\frac{1}{T}$がそのまま$e$の右肩に現れています。
このステップ応答をプロットすると、次のようになります。
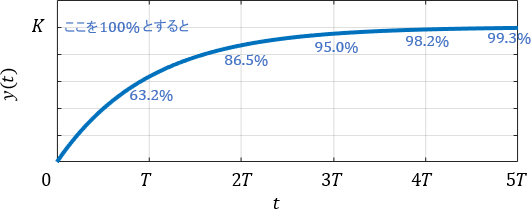

まず$0$が出力され、それがだいたい$5T$かけて$K$に収束していることが分かりますね。これも知っていれば、伝達関数を見ただけでステップ応答の挙動が瞬時に分かるようになります!
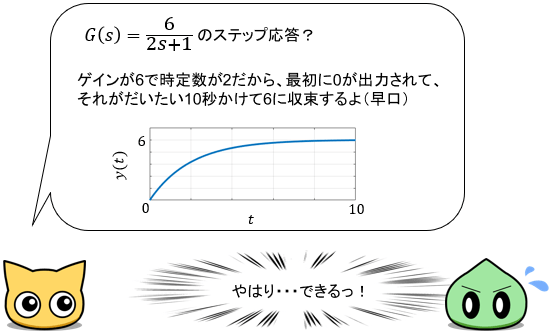

余裕があれば、時刻$T$にて出力が63.2%(だいたい2/3)まで立ち上がることも覚えておきましょう。
1次系の具体例
考慮するシステム
下図の機械システムを題材に、インパルス応答・ステップ応答の具体的なイメージを見ていきましょう。
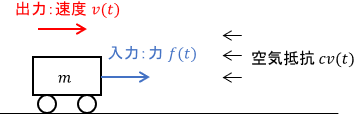

入力は台車に加わる力$f(t)$、出力は台車の速度$v(t)$、$m$は台車の質量、$c$は空気抵抗の係数です。この台車の運動方程式を求めると、次式が得られます。
$$m\dot{v}(t) = -cv(t) + f(t)$$
1階の微分方程式となっているので、これは1次系ですね。これをラプラス変換して出力についてまとめると、伝達関数が得られます。
$$V(s) = \ubg{\frac{1}{ms+c}}{伝達関数G(s)} F(s)$$
このシステムのゲイン$K$と時定数$T$を求めましょう。分母分子に$\frac{1}{c}$をかけます。
$$G(s)=\frac{\frac{1}{c}}{\frac{m}{c}s+1}$$
ゲインは$K = \frac{1}{c}$、時定数は$T = \frac{m}{c}$ですね!
※その他の1次系の例は、こちらの記事をご覧ください。
インパルス応答
このシステムのインパルス応答を考えましょう。インパルス応答なので、「最初に一瞬ガンッ!と大きな力を与え、あとは何もせずほっといたときの速度の挙動」ですね。
直感的には、最初に与えられた力によって台車が初速度を持ち、それが空気抵抗によって段々と0になる(台車が停止する)挙動となります。


先ほど求めたゲインと時定数から、インパルス応答の詳細な形状を調べましょう。
$$\begin{align}初速度&: \frac{K}{T}=\frac{1}{m}\\[5pt] 収束までの大体の時間&:5T=5\cdot \frac{m}{c}\end{align}$$
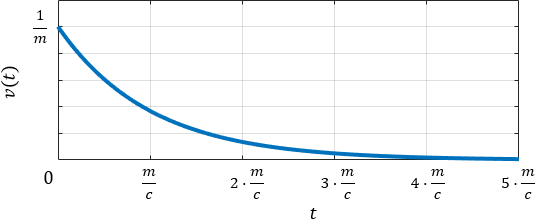

初速度$\frac{1}{m}$に注目すると、次の関係が分かります。
- 台車の質量$m$が大きいほど初速度は小さくなる(台車が重いほど動きにくい)
- 台車の質量$m$が小さいほど初速度は大きくなる(台車が軽いほど動きやすい)
収束時間$5\cdot \frac{m}{c}$に注目すると、次の関係が得られます。
- 台車の質量$m$が大きいほど収束時間は長くなる(台車が重いほど止まりにくい)
- 台車の質量$m$が小さいほど収束時間は短くなる(台車が軽いほど止まりやすい)
- 空気抵抗係数$c$が大きいほど収束時間は短くなる(空気抵抗が大きいほど止まりやすい)
- 空気抵抗係数$c$が小さいほど収束時間は長くなる(空気抵抗が小さいほど止まりにくい)
直感的にも納得のいく関係性ですね。
ステップ応答
次に、ステップ応答を考えましょう。ステップ応答なので、「一定の力を与え続けたときの速度の挙動」ですね。
直感的には、力が与えられるにつれて台車がどんどん加速し、やがて空気抵抗と釣り合う最終速度に収束する(一定速度で走り続ける)挙動となります。


先ほど求めたゲインと時定数から、ステップ応答の詳細な形状を調べましょう。
$$\begin{align}最終速度&: K = \frac{1}{c}\\[5pt] 収束までの大体の時間&:5T=5\cdot \frac{m}{c}\end{align}$$
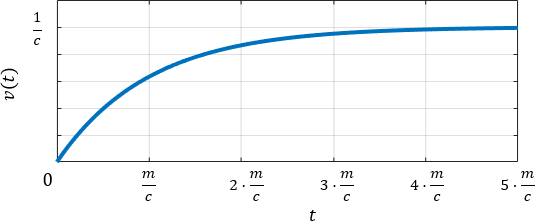

最終速度$\frac{1}{c}$に注目すると、次の関係が分かります。
- 空気抵抗係数$c$が大きいほど最終速度は小さくなる(空気抵抗が大きいほど動きにくい)
- 空気抵抗係数$c$が小さいほど最終速度は大きくなる(空気抵抗が小さいほど動きやすい)
こちらも直感的イメージと合致する関係性ですね。収束時間はインパルス応答と同じなので、先ほどと同じ関係性が成り立ちます。
1次系の使い方
ここからは、1次系のよくある使い方について解説していきます。
当然ですが、上の例のように対象が本質的に1次系である場合は、それを$G(s)=\frac{K}{Ts+1}$とモデリングし、分析・制御すればOKです。
ただ、1次系は非常にシンプルで扱いやすいため、これ以外にも様々な場面で利用されます。代表的な例は、遅れをお手軽に表現したい場面です。これについて、詳しく説明していきましょう。
インパルス応答やステップ応答の例を見て分かる通り、1次系の出力は、入力した信号が少し遅れた(なまった)形で出てきます。
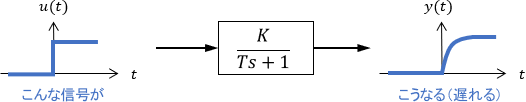
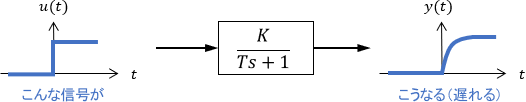
だから「1次遅れ系」とも呼ばれるわけですね。これを利用して、遅れをお手軽に表現することがよく行わます。
具体例で見ていきましょう。先ほどの台車を駆動するモーターの性能が悪く、電流を流してから力が発生するまでに少し遅れが生じるとします。
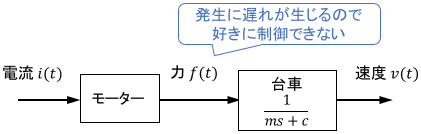

今、制御性能を高めるために、この遅れも数式モデルに組み込みたいとしましょう。このとき、モーターの特性を数式化してモデルに組み込めればよいのですが、モーターの特性がよく分かっていないとします。
こんなときは、下図のようにモーターを1次系で近似的にモデル化することで、とりあえずそれらしく信号の遅れを表現できます。
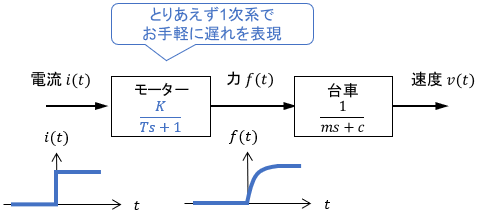

パラメータ設定も簡単で、ゲイン$K$で信号の倍率を、時定数$T$で遅れ量を設定するだけです。
当然、厳密にモーターの特性を数式化したほうがモデルの精度は高くなりますが、精度よりも式の単純性が求められる場合や、とりあえずお手軽に実装してざっくりと効果を確認したい場合は、このような近似が非常に有効です。
以上、1次系のインパルス応答・ステップ応答と、使い方の解説でした。
※こちらのページでは、周波数応答の観点から1次系の特性と使い方を解説していますので、合わせて覧ください。
- 1次系の伝達関数は、$G(s)=\frac{K}{Ts+1}$で表される。
- $K$はゲインと呼ばれる、出力の大きさを決めるパラメータ
- $T$は時定数と呼ばれる、出力の応答速度(収束時間)を決めるパラメータ
- 1次系は、信号の遅れをお手軽に表現するのに便利









コメント