システムの極は非常に重要なパラメータですが、なかなか具体的なイメージがつきにくいですよね。
このページでは極の正体を解明し、直感的意味・使い方・安定性との関係を具体例を通じて解説します。
※極の定義や導出方法が分からない方は、まずこのページをご覧ください
- 極は、システムのインパルス応答やステップ応答の中で、$e^{pt}$の右肩の係数$p$として現れる。
- 極の実部の正負を見ると、応答が収束するか発散するか、つまり安定性がわかる。
- 極の実部の絶対値が大きいほど、収束(or発散)が速い
- 複素極があると、応答が振動する。
- 複素極の虚部の絶対値が大きいほど、振動が速い
極の正体は「収束係数」だ!
システムの極は「システムの特性がギューッと凝縮された便利なパラメータ」でした。
では、具体的にどう凝縮されているのでしょうか?例題を通じて解明してみましょう。簡単な例として、次のような1次系を考えてみます。
$$Y(s)=\frac{1}{s-p}U(s)$$
システムの極はなんでしょうか?$p$ですね!
このシステムのインパルス応答とステップ応答を導出し、それらに対して極がどのように作用するのかを見てみましょう。
※インパルス応答・ステップ応答の詳細については、こちらのページをご覧ください
インパルス応答と極の関係
インパルス入力のラプラス変換は、$U(s)=1$ですので、これを入力した次式がシステムのインパルス応答です。
$$Y(s)=\frac{1}{s-p}\cdot 1 = \frac{1}{s-p}$$
これを逆ラプラス変換して、インパルス応答を時間$t$の関数として求めてみましょう。シンプルな関数なので、ラプラス変換の公式を使えば一発で変換できます。
$$y(t)=e^{pt}$$
極$p$が、$e^t$の右肩にそのまま現れましたね。
※ラプラス変換の基礎と各種公式については、こちらのページをご覧ください
この結果を用いて、極を様々な値に設定した場合のインパルス応答$y(t)=e^{pt}$をプロットしてみましょう。
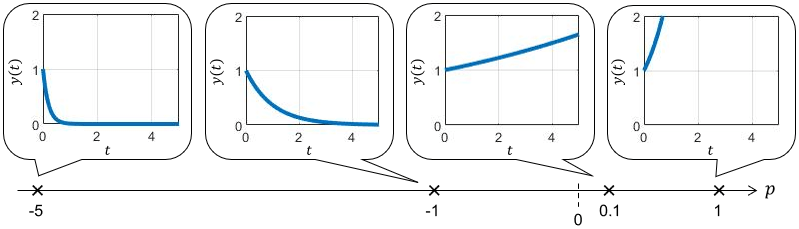
当然、指数関数のグラフそのものとなりますが、極と応答には次の関係がありますね。
- 極$p$が負なら、時間が経つにつれてインパルス応答が0に収束(システムは安定)
- 極$p$が正なら、時間が経つにつれてインパルス応答が∞に発散(システムは不安定)
- 極$p$の絶対値が大きいほど、収束(or発散)が速い
※システムの安定性については、こちらのページをご覧ください
ステップ応答と極の関係
ステップ入力のラプラス変換は$\frac{1}{s}$ですね。これを入力した次式がシステムのステップ応答です。
$$Y(s)=\frac{1}{s-p}\cdot \frac{1}{s}$$
これを逆ラプラス変換して、ステップ応答を時間の関数$t$として求めてみましょう。そのままでは変換できないので、いったん式を部分分数分解します。
$$Y(s)\ =\ \frac{1}{s-p}\cdot \frac{1}{s}\ =\ \frac{1}{p} \left( \frac{1}{s-p}-\frac{1}{s} \right) $$
※部分分数分解の方法については、こちらのページをご覧ください
後は各項を逆ラプラス変換するだけですね。
$$y(t)\ =\ \frac{1}{p} (e^{pt}-1) \ =\ \frac{1}{p} e^{pt}- \frac{1}{p}$$
先ほどと同じく、極$p$が$e^t$の右肩に現れました。
極を様々な値に設定した場合のステップ応答$y(t)$をプロットしてみましょう。
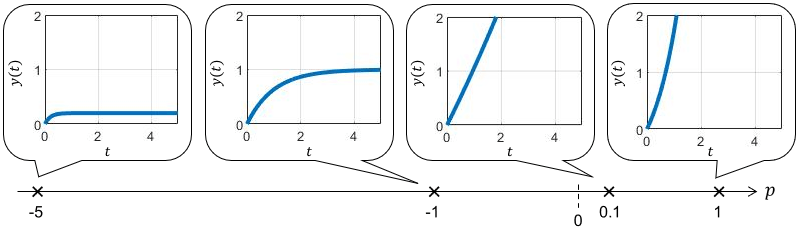
定数項があるので極によって収束先が変わっていますが、結局応答を支配しているのは時間に関する項$e^{pt}$なので、極と応答の関係性はインパルス応答と変わりません。
- 極$p$が負なら、時間が経つにつれてステップ応答が一定値に収束(システムは安定)
- 極$p$が正なら、時間が経つにつれてステップ応答が∞に発散(システムは不安定)
- 極$p$の絶対値が大きいほど、収束(or発散)が速い
以上の通り、極はインパルス応答・ステップ応答ともに時間に関する項$e^t$の右肩に$e^{pt}$という形で現れ、その値に応じて応答に影響を与えます。これが極の本質です!
極が複数あるシステムの場合
上で考えたのは極が1つだけの超単純なシステムでしたが、極が複数ある複雑なシステムでも考え方は同じです。これを具体的に確認していきましょう。
これまた簡単な例として、次の2次系を考えてみます。
$$Y(s)=\frac{1}{s-p_1} \cdot \frac{1}{s-p_2} U(s)$$
システムの極は、$p_1$と$p_2$の2つですね。このシステムのインパルス応答とステップ応答を導出し、極との関係を見ていきましょう。
※以降、$p_1 \neq p_2$であるとします
インパルス応答と極の関係
先ほどと同じく$U(s)=1$を代入し、逆ラプラス変換できるよう部分分数分解します。
$$Y(s)\ =\ \frac{1}{s-p_1} \cdot \frac{1}{s-p_2} \cdot 1\ =\ \frac{1}{p_1-p_2} \left( \frac{1}{s-p_1}-\frac{1}{s-p_2}\right)$$
各項を逆ラプラス変換したものが、時間$t$に対するインパルス応答です。
$$y(t)\ =\ \frac{1}{p_1-p_2} (e^{p_1 t} – e^{p_2 t}) \ =\ \frac{1}{p_1-p_2} e^{p_1 t} – \frac{1}{p_1-p_2} e^{p_2 t}$$
$e^t$の項が2つ現れ、それぞれの$e^t$の右肩に2つの極$p_1,p_2$が別々に現れました。結局、極が1つの場合と同じ結果が各項に現れ、それぞれの和が最終的なシステムの応答となるわけですね。
ステップ応答と極の関係
ここまでくるとだいたい想像がつきますが、$U(s)=\frac{1}{s}$を代入してステップ応答も見てみましょう。
$$\begin{align}Y(s)&=\frac{1}{s-p_1} \cdot \frac{1}{s-p_2} \cdot \frac{1}{s} \\\\ &= \frac{1}{p_1(p_1-p_2)} \cdot \frac{1}{s-p_1} – \frac{1}{p_2(p_1-p_2)} \cdot \frac{1}{s-p_2} + \frac{1}{p_1 p_2} \cdot \frac{1}{s}\end{align}$$
各項を逆ラプラス変換したものが、時間$t$に対するステップ応答です。
$$y(t) = \frac{1}{p_1(p_1-p_2)} e^{p_1 t} – \frac{1}{p_2(p_1-p_2)} e^{p_2 t} + \frac{1}{p_1 p_2}$$
インパルス応答の場合と同じく、2つの$e^t$の右肩に2つの極$p_1,p_2$が別々に現れ、それらの和が最終的なシステムの応答となりました。
これらをふまえると、インパルス応答・ステップ応答ともに、極と応答の関係性は次のようにまとめられます。
- 極が全て負なら、全ての項が一定値に収束(システムは安定)
- 極が1つでも正なら、応答が∞に発散(システムは不安定)
- 極の絶対値が大きいほど、収束(or発散)が速い
ここまで2次系を例に考えて来ましたが、それ以上の高次系でも本質は同じです。つまり、極の数だけ$e^{pt}$の項が現れ、上記関係性が成り立ちます。
モードと代表極
極から応答の収束・発散が読み取れることが分かりましたが、もう少し詳しい情報も読み取ってみましょう。上で考えた2次系のインパルス応答をもう一度考えます。
$$y(t) = \frac{1}{p_1-p_2} e^{p_1 t} – \frac{1}{p_1-p_2} e^{p_2 t}$$
各項のうち、$e^t$に極$p_1$が作用する項は極$p_1$のモード、極$p_2$が作用する項は極$p_2$のモードと呼ばれます。モードは「動作の成分」のようなイメージを持っておけばOKです。
$$y(t) = \ubg{\frac{1}{p_1-p_2} e^{p_1 t}}{極p_1のモード}\ \ubg{-\frac{1}{p_1-p_2} e^{p_2 t}}{極p_2のモード} $$
例えば$p_1=-1$、$p_2=-100$であるとすると、インパルス応答は次のようになります。

$p_1$のモードに対して$p_2$のモードは一瞬で収束しており、最終的な応答はほぼ$p_1$のモードと等しくなっていますね。このように、安定なシステムの応答は極の絶対値が小さなモードが支配的となり、絶対値が大きなモードはある程度無視できることが分かります。特に、絶対値が最も小さな極(影響力が最も大きい極)は、代表極と呼ばれます。
極を用いてシステムの動作を分析する際は、絶対値の小さなモードから見ていけばよいというわけですね。
複素極の意味
ここまで、極$p$が実数であることを前提に話を進めてきました。しかし実際は$p=a+bj$($j$は虚数単位)と、極が複素数で得られる場合も多いです。この場合も、これまでと同じく$e^{pt}$と極がそのまま右肩に現れると考えればOKです。

複素数が入った応答って現実にありえるの?
と思うかもしれませんが、もちろんありえません。応答を計算すると複素数の虚部がうまいこと打ち消され、最終的な解は必ず実数となるようになっています。これについて、詳しく見ていきましょう。
複素極のモード
再び、2次系のインパルス応答を例に考えます。
$$\begin{align}y(t) &= \frac{1}{p_1-p_2} e^{p_1 t} – \frac{1}{p_1-p_2} e^{p_2 t} \\\\ &= \frac{1}{p_1-p_2} (e^{p_1 t} – e^{p_2 t})\end{align}$$
ここでのポイントは、複素極は必ず次のように共役な形で現れることです。
$$\begin{align} p_1 = a &+ bj \\ p_2 = a &- bj \end{align}$$
これらをインパルス応答に代入し、式を整理してみます。
$$\begin{align}y(t) &= \frac{1}{(a+bj)-(a-bj)} \left\{ e^{(a+bj) t} – e^{(a-bj) t} \right\} \\\\ &= \frac{1}{2bj} \left( e^{at} e^{jbt} – e^{at} e^{-jbt} \right) \\\\ &= – \frac{j}{2b} e^{at} (e^{jbt} – e^{-jbt})\end{align}$$
オイラーの公式$e^{j\theta} = \cos \theta + j \sin \theta$を適用してさらに整理すると、
$$\begin{align}y(t) &= – \frac{j}{2b} e^{at} \Bigl[ \bigl\{ \cos (bt) + j \sin (bt) \bigr\}- \bigl\{ \cos (bt) – j \sin (bt) \bigr\} \Bigr] \\\\ &= – \frac{j}{2b} e^{at} \bigl\{ 2j \sin (bt) \bigr\} \\\\ &= \frac{1}{b} e^{at} \sin (bt) \end{align}$$
となります。確かに$j$がうまいこと消え、解が実数となりましたね。また、最終的に項が1つになりました。複素極は、共役な2つの極がセットで1つのモードを表していると解釈できます。
※ちなみに$b=0$のときは考えません。この場合、前提としている$p_1 \neq p_2$が成り立たず、そもそもインパルス応答が上式にならなくなるからです。
実部・虚部の役割
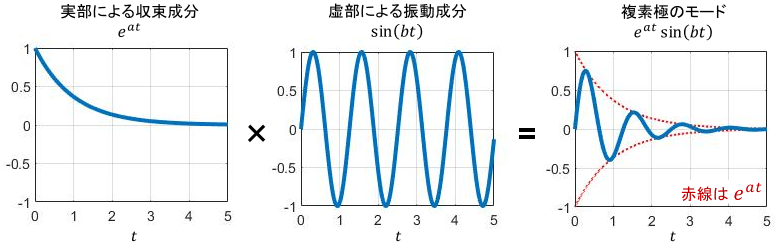
式の形を詳しく見てみましょう。おなじみの$e^t$の右肩には、極の実部$a$が乗っていますね。よって、極の実部$a$の役割はこれまでと同じであるといえます。
注目すべきは極の虚部$b$で、sin関数中の係数として現れていますね。すなわち、虚部の存在によってsin波状の振動成分が現れると解釈できます。$b$を様々に設定した際のsin関数の波形は次のようになります。

$b$の絶対値が大きいほど振動が速くなっていますね。また実部と異なり、$b$の正負は波形が裏返るだけで、挙動の傾向に大きな影響は与えていません。これらより、$b$は振動の周波数を決定するパラメータであると解釈できます。より具体的には、$b$は振動の角周波数となります。
※角周波数の詳細については、こちらのページをご覧ください
以上を踏まえて先ほど計算したインパルス応答の式 $\frac{1}{b} e^{at} \sin (bt)$を見返すと、複素極のモードは、実部による収束成分$e^{at}$と、虚部による振動成分$\sin(bt)$の積によってその特徴が決まることがわかります。
よって、複素極の値とモードの関係を複素平面上にまとめると、下図のようになります。
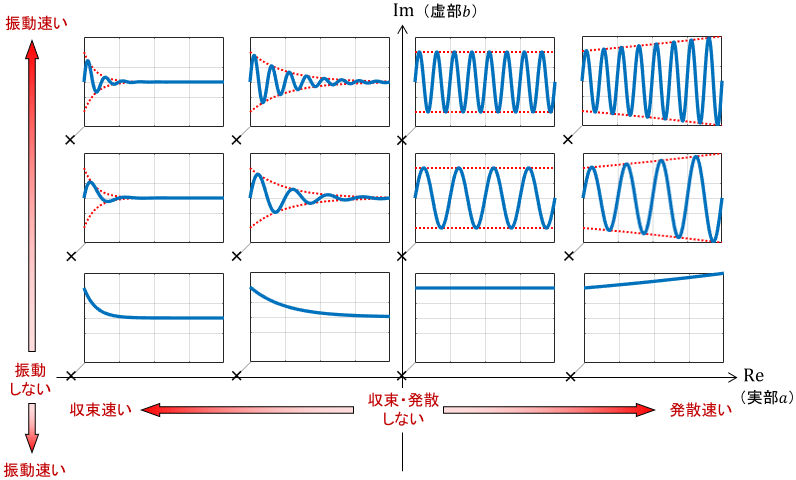
※スペースの関係から横軸から下半分は省略していますが、上半分を上下反転させたものを想像すればOKです。
また、ここでは2次系のインパルス応答を例に考えましたが、ステップ応答や、極がさらに多い高次系の場合も考え方は同じです。つまり、システムの極それぞれに応じたモードが上記と同じように現れ、それらの和が最終的なシステムの応答となります。
例えば1つの実極$p_1$と、2つの複素極$p_2,p_3$を持つシステムの応答は、モードを用いて次のように解釈できます。
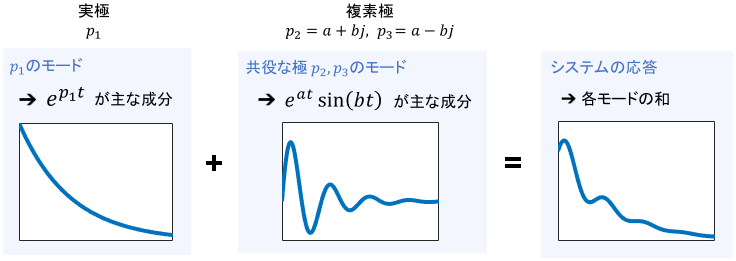
以上の議論から、実極・複素極に関わらず、極と応答の関係性は次のようにまとめられます。
- 極の実部が全て負なら、全てのモードが一定値に収束(システムは安定)
- 極の実部が1つでも正なら、応答が∞に発散(システムは不安定)
- 極の実部の絶対値が大きいほど、収束(or発散)が速い
- 極の虚部の絶対値が大きいほど、振動が速い
※高次系のイメージについては、こちらのページをご覧ください
例題で便利さを体感!
最後にちょっとだけ、極から情報を読み取る例題を考えてみましょう。極の便利さが体感できるはずです。
伝達関数が次式で表されるシステムを考えます。
$$G(s) = \frac{1}{(s+100)(s^2+2s+101)}$$
「分母=0」を$s$について解くと、システムの極は次のように求まります。
$$\begin{align} p_1 &= -100 \\ p_2 &= -1+10j \\ p_3 &= -1-10j \end{align}$$
この極からどのような情報が読み取れるでしょうか?次の通りですね。
- 極の実部が全て負なので、インパルス&ステップ応答は一定値に収束する(システムは安定)
- 各種応答は、実極$p_1$のモードと複素極$p_2, p_3$のモードの2つからなる
- $p_2, p_3$が代表極(実部の絶対値が他より大幅に小さい)。よって$p_1$のモードはほぼ無視できる
- $p_2, p_3$のモードは、角周波数10[rad/s]で振動しながら、$e^{-t}$のペースで収束する
極だけからひと目でこれだけの情報が分かれば、非常にありがたいですね。
以上、極の直感的意味・使い方・安定性との関係についての解説でした。
- 極は、システムのインパルス応答やステップ応答の中で、$e^{pt}$の右肩の係数$p$として現れる。
- 極の実部の正負を見ると、応答が収束するか発散するか、つまり安定性がわかる。
- 極の実部の絶対値が大きいほど、収束(or発散)が速い
- 複素極があると、応答が振動する。
- 複素極の虚部の絶対値が大きいほど、振動が速い











コメント