このページでは次のように、伝達関数で表された単体のシステムに対する様々な安定判別法を解説します。
それぞれに利点・欠点がありますので、しっかりと使い分けられるようにしておきましょう!
※システムの安定性の意味については、こちらのページをご覧ください
| 安定判別法 | お手軽さ | 得られる情報の多さ |
|---|---|---|
| 微分方程式の求解による判別法 | ✕ | ◎ |
| 極による判別法 | ○ | ○ |
| 特性方程式の係数による判別法 | ◎ | ✕ |
| ラウス=フルビッツの安定判別法 | △ | △ |
- 「これだけ使っておけばOK!」という方法はなく、ケースバイケースで使い分けるのがベスト
方法1:微分方程式の求解による判別法
判別方法
システムの安定性をざっくりと説明すると、「何も入力せずにほっといたら、出力が収束するかどうか」でしたね。
よって最も原始的な方法としては、システムの方程式を直接解いて、出力が収束するかどうかを確認する方法が考えられます。コンピュータでシステムの挙動を計算(シミュレーション)してみる場合もこれに含まれますね。


利点
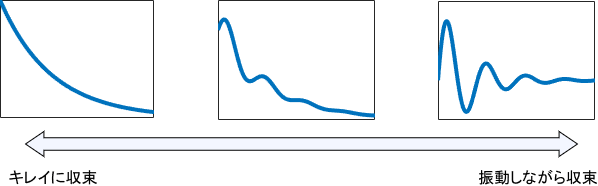
この方法の利点は、システムの具体的な挙動を直接確認できることです。システムが安定だとしても収束に時間がかかったり、振動的な挙動が生じたりする場合がありますが、それらを直接確認できれば設計や評価がしやすいですよね。

欠点
一方の欠点は、方程式を解くのが面倒なことです。ラプラス変換を使えば微分方程式の求解が少し楽になるとはいえ、逆ラプラス変換時に部分分数分解がたくさん出てくるので、やはり手間は残るんですよね…。
※ラプラス変換については、こちらのページをご覧ください
よって、できれば方程式を直接解く前に安定性を判別したいですよね。そして安定と分かったときだけ方程式を解き、より詳しい挙動を解析できれば、手間が減って効率的です。
そこで使えるのがシステムの極です。
方法2:極による判別法
判別方法
極は「微分方程式を解かなくてもシステムの挙動がある程度分かる、便利なパラメータ」でした。この極を用いると、システムの安定性を次のように判別できます。
システムの極が$p_1 = a_1+b_1j, \ p_2=a_2 + b_2 j,\ \cdots$であるとき、
- 極の実部$a_1, a_2, \cdots$が全て負なら、そのシステムは安定
- 極の実部$a_1, a_2, \cdots$が1つでも正(0以上)なら、そのシステムは不安定
※これで安定性が判別できる理由はこちらの記事で詳しく解説していますので、合わせてご覧ください。
利点
この方法の利点は、微分方程式を直接解くことなく、極の実部の符号を見るだけでシステムの安定性を判別できることです。面倒な逆ラプラス変換から解放されるわけですね。
他の手法と比較して利点・欠点のバランスがよいのも特徴です。
欠点
一方の欠点は、微分方程式を直接解く場合よりは、システムの応答を直感的にイメージしにくいことです。
とはいえ、大体の収束速度や振動周波数は極から一目で分かります(詳しくは先ほどのリンクをご覧ください)。よって、ざっくりと性質を見たいだけの設計初期段階などであれば極の情報だけで十分な場合が多く、大きな欠点ではないと言えます。
またもう一つの欠点として、ときには極を求めることすら面倒となることが挙げられます。
システムの極を求める特性方程式は、システムの次数に応じて複雑化します。例えば、対象とするシステムの特性が6階の微分方程式で表されるとすると、その特性方程式は6次方程式となります。
$$s^6 + a_5 s^5 + a_4 s^4 + a_3 s^3 + a_2 s^2 + a_1 s + a_0 = 0$$
これを解くのはめんどくさいですよね…。ラプラス変換が面倒だから極を使うわけですが、極の導出も面倒であれば使う意味が薄れてきます。ただ、今どきはコンピュータが一瞬で極を計算してくれますので、この欠点もほぼ解消されています。
※例えばこちらのサイトでは、入力した伝達関数に対し、極を含め様々な性質を自動で計算してくれます。


コンピュータ使うのもめんどくさいんですけど…
…そんなあなたには、より簡易的な方法をご紹介しましょう
方法3:特性方程式の係数による判別法
判別方法
特性方程式(つまり伝達関数の分母)の中で、$s$に付いている係数が1つでも負であれば、そのシステムは不安定であることが知られています。
例えば今考えているシステムの伝達関数が
$$G(s)=\frac{1}{s^6+5s^4-3s^3+7s^2+5s+6}$$
であれば、$s^3$の係数が負であるので、このシステムは不安定であると一瞬で分かります。
利点
利点は当然、一切の計算なしに不安定なシステムをひと目で見つけられることです。
先ほどの伝達関数の極を計算しようとすると6次方程式を解く必要がありますが、そんなことせずとも一発で不安定だと突き止められましたね。超お手軽です!
欠点
ただし、この判別基準は不安定性の十分条件に過ぎないため注意が必要です。つまり、$s$に付いている係数がすべて正であっても、そのシステムは安定とは言えません。
- 特性方程式の係数が1つでも負 ⇒ 絶対に不安定
- 特性方程式の係数が全て正 ⇒ 安定性・不安定どちらもありうる
例えば伝達関数が
$$G(s)=\frac{1}{s^6+5s^4+3s^3+7s^2+5s+6}$$
であれば係数が全て正なので、特性方程式を実際に解いて極の実部の正負を調べないと、安定性はわかりません。
方法4:ラウス=フルビッツの安定判別法
極を用いて安定判別する際、結局知りたいのは極そのものではなく「極の実部の正負」でした。
よって、極の実部の正負だけを手計算で判別する方法として、19世紀にラウスの安定判別法とフルビッツの安定判別法が考案されました。これを用いると、特性方程式を解くよりは手軽に実部の正負を判別できます。
※ラウスの安定判別法とフルビッツの安定判別法は、具体的な方法は違えど本質的に同じことをしているため、両者をまとめて「ラウス=フルビッツの安定判別法」と呼ぶこともあります。
…が、前述の通り今はコンピュータで簡単に極を計算できるので、実用場面でこれらの手法を用いることはあまりありません。結局いちいち手計算するなら、極を計算するためのソフトやプログラムを準備したほうが効率がいいからです。一度準備してしまえば、様々なシステムに流用できますからね。
よって、詳しい説明は一旦省略したいと思います。この手法が必要となるのは制御工学の筆記試験時くらいかと思いますが、そのような方は制御工学の教科書を持っていると思いますので、そちらの詳しい説明をご参照ください。
以上、様々な安定判別法についての解説でした。「これだけ使っておけばOK!」という方法はなく、ケースバイケースで柔軟に使い分けるのがベストですので、各手法の利点・欠点をしっかり理解しておきましょう。
※ちなみに、次のようなフィードバック制御システムの安定性は「内部安定性」という観点で考える必要があり、上記方法がそのまま適用できるとは限らないため注意が必要です。
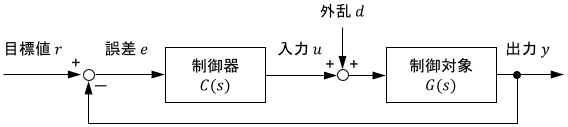

内部安定性とその判別法については、こちらのページをご覧ください。
| 安定判別法 | お手軽さ | 得られる情報の多さ |
|---|---|---|
| 微分方程式の求解による判別法 | ✕ | ◎ |
| 極による判別法 | ○ | ○ |
| 特性方程式の係数による判別法 | ◎ | ✕ |
| ラウス=フルビッツの安定判別法 | △ | △ |
- 「これだけ使っておけばOK!」という方法はなく、ケースバイケースで使い分けるのがベスト







コメント