
零点を持つシステムってどんなの?
という疑問に答えるため、このページでは実用上よく見る、零点を持つシステムを紹介します。
※零点の定義や導出方法については、こちらのページをご覧ください
- 数式モデルに入力の時間微分が現れるシステムは、零点を持つ
- 零点を持たないシステム同士でも、それらを並列結合・フィードバック結合すると零点が生じる
もともと零点を持つシステムの例
伝達関数の分子に$s$を持つシステムは零点を持ちます。伝達関数の分子の$s$の次数は、数式モデルの中で入力を微分する回数に等しくなるのでしたね。よって、数式モデルに入力の時間微分が現れるシステムは零点を持つことになります。
以下、そのようなシステムの例を見ていきましょう。
機械システムの例
次のようなばねダンパ系は、零点を持ちます。
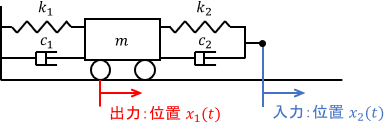
入力は右側のばね・ダンパ端の位置$x_2(t)$、出力は台車の位置$x_1(t)$、$m$は台車の質量、$k_1,k_2$はばね定数、$c_1,c_2$は粘性係数です。この台車の運動方程式は次式となります。
$$m\ddot{x}_1 = -k_1 x_1 – c_1 \dot{x}_1 – k_2 (x_1 – x_2) – c_2 (\dot{x}_1 – \dot{x}_2)$$
これをラプラス変換して出力についてまとめると、伝達関数が得られます。
$$\begin{gather}(ms^2+c_1 s + c_2 s + k_1 + k_2)X_1(s) = (c_2 s + k_2) X_2(s) \\\\ X_1(s) = \ubg{\frac{c_2 s + k_2}{ms^2+ (c_1 + c_2) s + (k_1 + k_2)}}{伝達関数}X_2(s)\end{gather}$$
確かに零点$-\frac{k_2}{c_2}$を持つことが分かりますね。
直感的なイメージを考えてみましょう。今、右側のダンパの影響で、台車に加わる力が入力$x_2$の速度にも依存します。そのため運動方程式に入力の微分$\dot{x}_2$が生じ、結果的にシステムが零点を持つわけですね。
同様の理由で、次のように台車が2つ繋がったシステムも零点を持ちます。
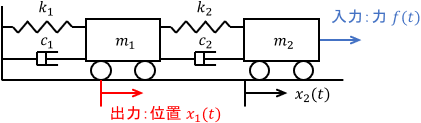
このシステムの伝達関数は次式となります。確かに零点$-\frac{k_2}{c_2}$を持ちますね。
$$ X_1(s) = \ubg{ \frac{c_2 s + k_2}{\Bigl\{ m_1 s^2 + (c_1 + c_2)s + (k_1 + k_2)\Bigr\} (m_2 s^2 + c_2 s + k_2) – (k_2 + c_2 s)^2} }{伝達関数} F(s)$$
※詳しい導出は、こちらのページをご覧ください
電気システムの例
次のようなRLC回路は、零点を持ちます。

入力は電圧$v_{in}(t)$、出力は電圧$v_{out}(t)$、$i(t)$は回路を流れる電流、$R_1,R_2$は抵抗値、$L$はコイルのインダクタンス、$C$はコンデンサの容量です。コンデンサ両端の電圧を$v_C$とすると、電流$i(t)$は次式で求められます。
$$i = C\dot{v}_{C}$$
また、キルヒホッフの法則より$v_{in},v_{out}$は次のように計算できます。
$$\begin{align} v_{in} &= (R_1+R_2) i + L \dot{i} + v_C \\ &= (R_1 + R_2)C\dot{v}_C + LC\ddot{v}_C + v_C\\\\v_{out} &= R_2 i + v_C \\ &=R_2 C \dot{v}_C + v_C \end{align}$$
それぞれをラプラス変換します。
$$\begin{align} V_{in}(s) &= \bigl\{ LCs^2 + (R_1+R_2)Cs + 1\bigr\}V_C(s)\\[5pt] V_{out}(s) &= (R_2 C s + 1)V_C(s) \end{align}$$
あとは出力についてまとめると、伝達関数が得られます。
$$V_{out}(s) = \ubg{ \frac{R_2 C s + 1}{LCs^2 + (R_1+R_2)Cs + 1} }{伝達関数}V_{in}(s)$$
零点$-\frac{1}{R_2 C}$を持ちますね。色々式変形しましたが、これも結果的に出力$v_{out}(t)$が入力の時間微分$\dot{v}_{in}(t)$にも依存するためです。
システムの結合により零点が生じる例
並列結合により零点が生じる例
それぞれ極$p_1,p_2$を持つ1次系$G_1(s),G_2(s)$を考えましょう。
$$G_1(s) = \frac{1}{s-p_1}, \qquad G_2(s) = \frac{1}{s-p_2}$$
これらのシステムは零点を持ちませんが、これらを並列結合すると零点が生じます。
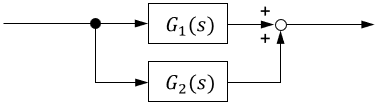
$$G_{全体}(s)=G_1(s) + G_2(s) = \frac{1}{s-p_1} + \frac{1}{s-p_2} = \frac{2s-p_1-p_2}{(s-p_1)(s-p_2)}$$
零点は$ \frac{p_1+p_2}{2}$ですね。
このケースが生じる具体例としては、中身をいじれない既存のシステムや制御器に対し、それを補正するような制御器を新たに加える場合などが挙げられます。

フィードバック結合により零点が生じる例
先ほどの$G_1(s),G_2(s)$をフィードバック結合しても、零点が生じます。
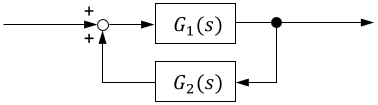
$$G_1(s) = \frac{1}{s-p_1}, \qquad G_2(s) = \frac{1}{s-p_2}$$
$$G_{全体}(s)=\frac{G_1(s)}{1+G_1(s)G_2(s)} = \frac{s-p_2}{1+(s-p_1)(s-p_2)}$$
零点$p_2$が生じましたね。
以上、零点を持つシステムの例でした。零点が生じるパターンを知っておくことで、システムの設計や分析に見通しがつきやすくなりますよ!
特に不安定零点(実部が0以上である零点)が発生するとシステムに悪影響を及ぼす場合があるため、設計時には注意が必要です。詳しくはこちらのページで解説していますので、合わせてご覧ください。

- 数式モデルに入力の時間微分が現れるシステムは、零点を持つ
- 零点を持たないシステム同士でも、それらを並列結合・フィードバック結合すると零点が生じる





コメント