システムの零点は極以上にイメージしにくいパラメータですが、多くの重要な性質を持っています。
このページでは零点の正体を解明し、直感的な意味について解説します。また、極零相殺・不安定零点・逆振れについても解説します。
※零点の定義や導出方法については、こちらのページをご覧ください
- 零点が、ある極に近ければ近いほど、その極の影響が大きく打ち消される
- 零点が、ある極に一致すると、その極の影響が完全になくなる
- 不安定極を零点で打ち消そうとしてはダメ(不安定な極零相殺)
- 不安定零点は基本的にシステムに悪影響を及ぼすので、持たないほうが良い
零点の正体は「極打消し機」だ!
例題を通じて、零点の正体を解明してみましょう。簡単な例として、次のような2次系を考えてみます。
$$Y(s)=\ubg{\frac{s-z}{(s-p_1)(s-p_2)}}{伝達関数G(s)}U(s)$$
システムの極は$p_1$と$p_2$、零点は$z$ですね。
上式の$G(s)$は、零点を持つ厳密にプロパーな伝達関数の最小単位なので、零点付き2次遅れ要素と呼ばれることもあります。
※「厳密にプロパーな伝達関数」とは「分子の次数<分母の次数」を満たす伝達関数のことです。古典制御で扱う伝達関数のほとんどは厳密にプロパーです。詳しくはこちらのページをご覧ください。
零点が極に等しい場合
まず、$z=p_1$である場合の作用を考えましょう。このとき、伝達関数は次のように変形されます。
$$G(s)=\frac{s-z}{(s-p_1)(s-p_2)}=\frac{s-p_1}{(s-p_1)(s-p_2)}=\frac{1}{s-p_2} \quad \color{green}{p_1が消えた!}$$
分子と分母が約分され、極$p_1$が伝達関数から消えてしまいましたね。このことから、端的に言うと零点は極の影響を打ち消す「極打消し機」であると言えます。
$z=p_2$の場合も同様に、極$p_2$が消えますね。よって、1つの零点で打ち消せる極は1つだけであると分かります。
零点と極が異なる場合
零点と極が異なる場合は、どのように作用するでしょうか?これを確かめるため、伝達関数を変形してみます。
$$G(s)=\frac{s-z}{(s-p_1)(s-p_2)}=\ \cdots \ = \frac{p_1-z}{p_1-p_2}\cdot \ubg{\frac{1}{s-p_1}}{p_1のモード}-\frac{p_2-z}{p_1-p_2}\cdot \ubg{\frac{1}{s-p_2}}{p_2のモード}$$
途中の式変形は飛ばしましたが、結局極$p_1$のモードの係数として$p_1$と$z$の差$(p_1-z)$が、極$p_2$のモードの係数として$p_2$と$z$の差$(p_2-z)$が作用していますね。
以上から、零点は次のように伝達関数に作用することが分かります。
- 零点が、ある極に近ければ近いほど、その極の影響(モード)が大きく打ち消される
- 零点が、ある極に一致すると、その極の影響(モード)が完全になくなる
※「極$p$のモード」は「極$p$が作り出す動作の成分」だと思ってください。モードについてはこちらのページで解説していますので、合わせてご覧ください。
細かいことを言うと、上記$\frac{1}{s-p}$は伝達関数の一部であり、実際の動作(出力)ではありません。よって、厳密には「$p$のモード」ではなく「伝達関数の中で$p$のモードを作り出す成分」ですが、簡単のため本ページでは「$p$のモード」と表記しています。
不安定な極零相殺と、それが悪い理由
上記より、零点によって極の影響を打ち消せることが分かりました。

ほーん。じゃあもし制御対象が不安定でも、制御器の零点で不安定極を打ち消せばシステム全体を安定化できるんだな。
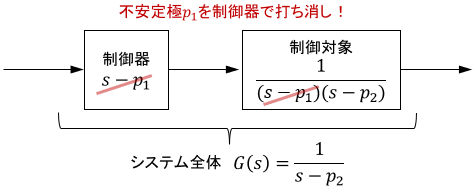
と思うかもしれません。理論上はその通りですが、これは絶対に避けるべきです。このように不安定極と不安定零点が打ち消し合うことは不安定な極零相殺と呼ばれ、非常に危険であるとされています。この理由を説明していきましょう。
※実部が0以上である極と零点のことを、それぞれ不安定極・不安定零点と呼びます。不安定極は出力を無限大に発散させる作用を持つため、システムを不安定にしてしまいます。詳細は、先ほど紹介した極のページをご覧ください。
理由1:現実にはキレイに相殺できない
当然ですが、上図のように零点で極を打ち消すためには、零点と極が完全に同じでなくてはなりません。しかし、数式モデルには必ず誤差があるため、現実に極と零点が完全に一致することはまずありえません。
もし不安定極$p_1$と零点$z$が非常に小さな差$(p_1-z)$を持つ場合、何が起こるのかを見てみましょう。先ほどと同様に伝達関数を変形し、各モードを確認します。
$$G(s)=\frac{s-z}{(s-p_1)(s-p_2)}= \ubg{\frac{p_1-z}{p_1-p_2}}{超小さい数}\cdot \ubgd{\frac{1}{s-p_1}}{不安定モード}{→\infty に発散}-\frac{p_2-z}{p_1-p_2}\cdot \ubgd{\frac{1}{s-p_2}}{安定モード}{→0に収束}$$
確かに不安定極$p_1$のモードには非常に小さな数$(p_1-z)$がかかります。しかし不安定な$p_1$のモードは時間とともに無限大に発散するので、小さな数をかけたところで発散を食い止めることはできません。
よって零点によって不安定極を打ち消し、システムを安定化させることは、現実的には不可能です。
理由2:内部安定性が崩れる
次のようなフィードバック制御システムの本質的な安定性は、内部安定性と呼ばれます。
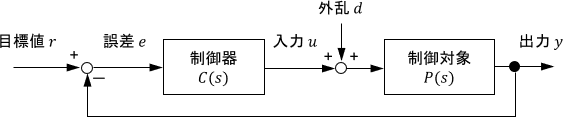
※内部安定性の詳細については、こちらのページをご覧ください
そして、このシステムの中に不安定な極零相殺が存在すると、内部安定性が崩れてしまうことが知られています。
面白いのが、もし不安定極と不安定零点を完全に相殺できたとしても安定性が崩れてしまう所です。「信号がフィードバックループをグルグル回るうちに発散してしまう」とイメージすればよいでしょう。
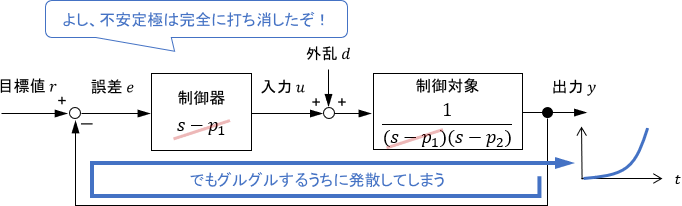
こうなるとシステムが使い物にならなくなるため、この点からも不安定な極零相殺は避けるべきであると言えます。
理由3:不安定零点は悪さをする
不安定な極零相殺があるということは、システムが不安定極と不安定零点を持つことになります。
不安定極が悪いのは前述の通りですが、後で説明するように、不安定零点もシステムに悪影響を及ぼします。よって不安定極のデメリットを打ち消すどころか、さらなるデメリットを付加してしまうと言えます。
以上のように、不安定な極零相殺は「悪者同士が手を組んでお互いの存在を隠している」ような状態であるため、意図的に起こさせないのはもちろん、意図せず生じていないかも注意深く確認が必要です。
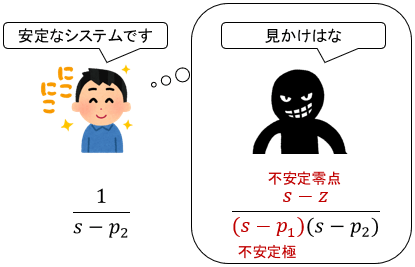
ちなみに、安定極と安定零点の相殺は何の問題もありません。もともと無害なので、打ち消し合おうが残ろうが構わないというわけですね。
不安定零点が悪い理由
ここからは、不安定零点がシステムに及ぼす悪影響について解説していきましょう。
ステップ応答にオーバーシュート・アンダーシュートが生じる
不安定零点は、ステップ応答にオーバーシュートやアンダーシュート(逆振れ)を引き起こすことが知られています。
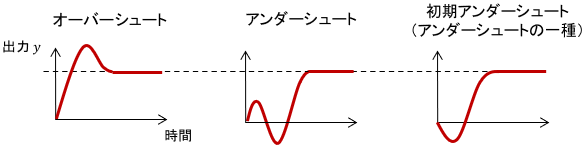
具体的には、プロパーなシステム$G(s)$のステップ応答に対して、次のように影響を与えます。
- $G(s)-G(0)$が実数の不安定零点を1つでも持つと、ステップ応答にオーバーシュートが生じる
- $G(s)$が実数の不安定零点を1つでも持つと、ステップ応答にアンダーシュートが生じる
- $G(s)-G(\infty)$が実数の不安定零点を奇数個持つと、ステップ応答に初期アンダーシュートが生じる
証明は省略しますが、とにかく不安定零点を持つメリットはなさそうですね。
逆システムが不安定になる
もう1つ、不安定零点を直感的にイメージできる例を紹介します。
伝達関数を逆算して、希望の出力軌道を実現するフィードフォワード入力を計算することを考えましょう。当然、逆システム(伝達関数の逆関数)を考えればOKですね。
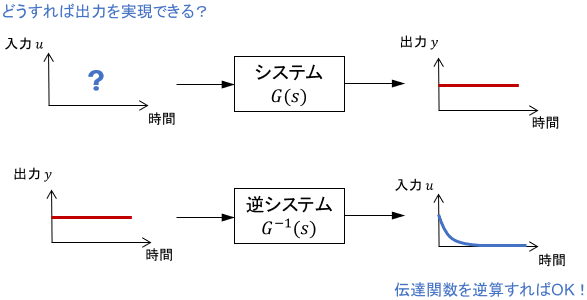
逆システムは次式で得られます。
$$元システムG(s)=\frac{零点に関する部分}{極に関する部分}\ \color{red}{\xrightarrow{\large 上下反転!}} \ 逆システムG^{-1}(s)=\frac{極に関する部分}{零点に関する部分}$$
ここで注目したいのは、逆システム$G^{-1}(s)$の極は元システムの零点であるという点です。つまり、元システムが不安定零点を持つと逆システムは不安定となります。
不安定なシステムは、適切に入力を与えないと出力が無限大に発散するシステムでした。よって不安定な逆システムを用いて入力を逆算すると、無限大の入力が必要となるケースが多発します。一言でいうと、大抵の出力軌道は実現不可能になってしまうということですね。
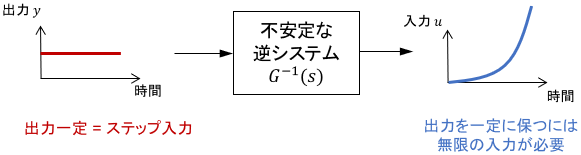
当然、適切に出力軌道を与えれば発散しない入力が求まりますが、その設計難度は格段に上がります。不安定なシステムを制御するのが難しいのと同じですね。この意味でも、不安定零点はシステムに悪影響を及ぼすといえるでしょう。
以上、零点の正体と直感的な意味の解説でした。零点を持つシステムを取り扱う際は、上記イメージを思い出してくださいね!
※こちらのページでは零点を持つシステムの具体例を紹介していますので、合わせてご覧ください。
- 零点が、ある極に近ければ近いほど、その極の影響が大きく打ち消される
- 零点が、ある極に一致すると、その極の影響が完全になくなる
- 不安定極を零点で打ち消そうとしてはダメ(不安定な極零相殺)
- 不安定零点は基本的にシステムに悪影響を及ぼすので、持たないほうが良い








コメント
>具体的には、プロパーなシステムG(s)のステップ応答に対して、次のように影響を与えます。
>
>・G(s)−G(0)が実数の不安定零点を1つでも持つと、ステップ応答にオーバーシュートが生じる
>・G(s)が実数の不安定零点を1つでも持つと、ステップ応答にアンダーシュートが生じる
>・G(s)−G(∞)(厳密にプロパーなシステムならG(s))が実数の不安定零点を奇数個持つと、
> ステップ応答に初期アンダーシュートが生じる
>証明は省略しますが、とにかく不安定零点を持つメリットはなさそうですね。
上記の証明について知りたいのですが、証明が記載されている書籍等あれば、ご教示頂けますでしょうか?
零点とオーバーシュート/アンダーシュートの関係については、こちらの記事によくまとまっています。簡単な証明もありますので、ご参照ください。
https://people.duke.edu/~hpgavin/SystemID/References/HoaggBernsteinNonMinimumPhaseZero-CSM-2007.pdf
(リンクが切れていたらこちら)
https://ieeexplore.ieee.org/document/4213166
さらに厳密な証明が必要であれば、この記事の参考文献を参照すればよいかと思います。
すみません、
G(s)−G(0) や G(s)−G(∞)
というのはどういう意味なんでしょうか
制御対象の伝達関数の「S」の部分が0になるとはどういうことでしょうか
lim t→∞をラプラス変換して lim S→0 となるということでしょうか
前にあった、誤差の最終値の意味でしょうか
返信が遅くなり、すみません。
G(0)は伝達関数G(s)にs=0を代入した結果、という意味です。
G(∞)はG(s)に対してs→∞の極限をとったもの、という意味です。