内部安定性は、フィードバック制御システムの本質的な安定性を表す特性です。
次のようなシンプルなシステムであれば、システムの安定性は、その極から判別できるのでした。
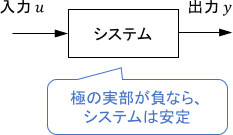
ただ、フィードバック制御システムには様々な信号が含まれるため、同様に取り扱うだけでは不十分となってしまいます。
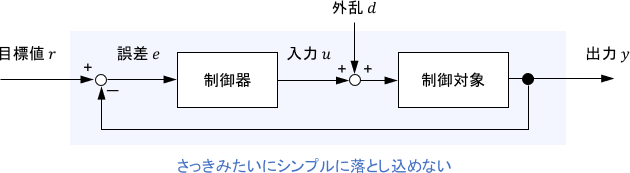
この記事では、フィードバック制御システムの内部安定性の意味と、判別方法を詳しく解説します。
※システムの安定性の基礎と、極を用いた安定判別については、こちらのページをご覧ください。
- システムに加わるすべての入力信号に対して、システム内のすべての信号が発散しないならば、そのシステムは内部安定であるという
- 内部安定でなければ、システムは使い物にならない
- 不安定な極零相殺がなく、かつ閉ループ伝達関数が安定であれば、そのシステムは内部安定である
- 不安定な極零相殺があるならば、そのシステムは内部安定でない
内部安定性とは
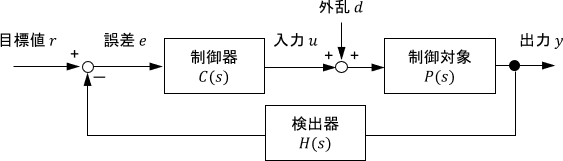
次のような、外乱を含むフィードバック制御システムの安定性を考えましょう。
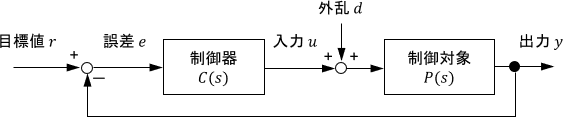
制御の目的は、出力$y$を目標値$r$に追従させることです。よって、制御性能を調べるのに最も重要なのは、目標値$r$に対する出力$y$の性質、すなわち閉ループ伝達関数の性質となりますね。
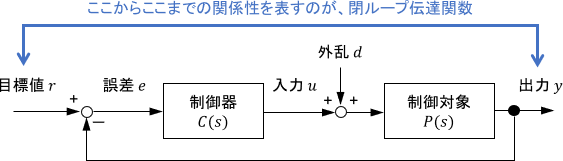
※閉ループ伝達関数の詳細については、こちらのページをご覧ください。
安定性を考える際も、閉ループ伝達関数は極めて重要です。もし閉ループ伝達関数が不安定であれば、目標値$r$に対して出力$y$が発散してしまうことになるため、使い物にならなくなってしまいます。


…うん。だから、閉ループ伝達関数が安定であればOKなんでしょ?
と思うかもしれませんが、それだけではOKではないのがポイントです。
目標値$r$と出力$y$はフィードバック制御において非常に重要な信号ですが、このシステムには他にも信号がありますよね。外から加わる信号としては外乱$d$もありますし、入力$u$もシステムの内部信号として存在します。
よって、たとえ目標値$r$に対して出力$y$が発散しなくても、例えば外乱$d$に対して出力$y$が発散してしまうのであれば、そのシステムは使い物にならないことになります。
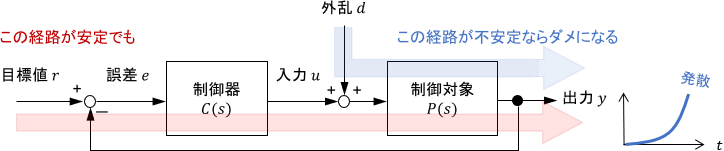
内部安定性は、このようなことが起こらないことを表す特性です。
上記が起こらないためには、システムに加わる「すべての」入力信号に対して、システム内の「すべての」信号が安定である(発散しない)必要があります。
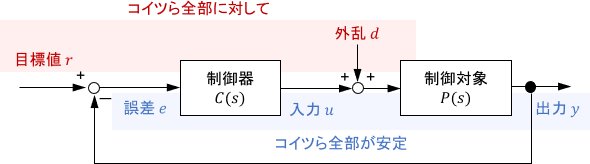
これが満たされるとき、そのシステムは「内部安定である」と呼ばれ、初めて安心して使えるというわけです。
このことから、内部安定性はフィードバック制御システムの本質的な安定性を表す特性であると言えるでしょう。
※本ページでは、特に利用頻度の高い上図の構成のシステムを対象に解説していきますが、内部安定性そのものはどんなシステムにも適用可能です。つまり、どんなシステムであれ「システムに加わるすべての入力信号に対して、システム内のすべての信号が安定」でさえあれば、そのシステムは内部安定です。
不安定な極零相殺と内部安定性
内部安定性において特に注意が必要となるのは、制御対象と制御器の間に不安定な極零相殺があるときです。
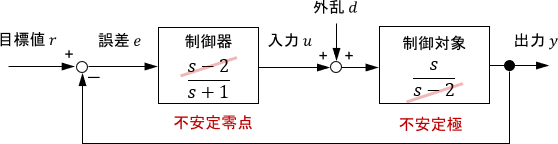
※あるシステムの不安定極が、他のシステムの不安定零点によって相殺されることを「不安定な極零相殺」と呼びます。詳細については、こちらのページをご覧ください
というのも、不安定な極零相殺があるときには、上で示したような「閉ループシステムは一見安定そうに見えるけど、実はシステム全体は内部安定ではない(システム内の一部の信号が発散する)」という状況が起こりうるためです。
このようなことが起きる例を見てみましょう。伝達関数が次のようなシステムを考えます。
$$制御器\ C(s)=\frac{s-1}{s} ,\qquad 制御対象\ P(s)=\frac{1}{s-1}$$
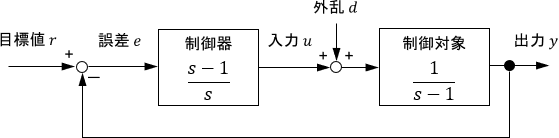
制御対象$P(s)$が不安定な極を持っていますが、それが制御器$C(s)$の零点によって打ち消されていますね。よって、不安定な極零相殺が存在します。
このシステムに、入力としてステップ状の目標値$r$と外乱$d$を与えてみましょう。
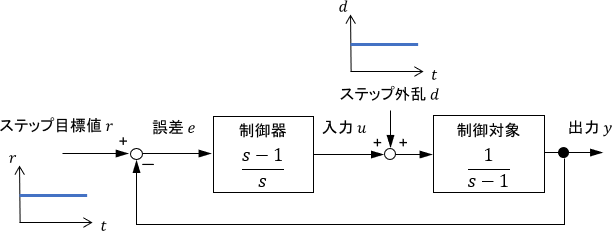
「外乱あり」と「外乱なし」それぞれの場合でシミュレーションしたときの、入出力信号の様子がこちらです。
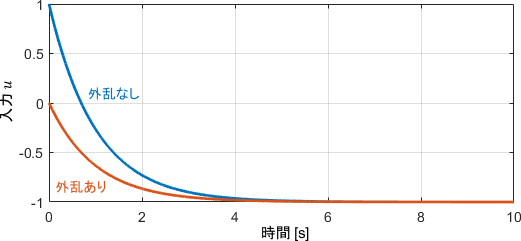
まず入力信号$u$に注目すると、外乱の有無に関わらず、発散することなく制御できていることが分かります。
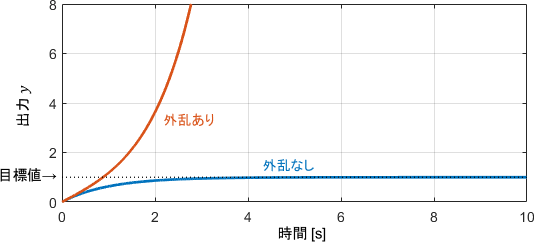
一方で出力信号$y$に注目すると、外乱$d$がない場合、すなわち目標値$r$だけが与えられた場合は発散していません。よって、閉ループ伝達関数は安定(=$r$に対して$y$は安定)であることが分かります。
しかしながら、外乱$d$も作用した場合は出力$y$が発散してしまっています(=$d$に対して$y$は不安定)。よって、不安定な極零相殺を持つこのシステムは「閉ループシステムは一見安定そうに見えるが、実はシステム全体は内部安定ではない」という状態になっていることが分かります。
内部安定性の確かめ方

ほーん。内部安定のイメージはだいたい分かったけど、内部安定かどうかはどうやったら確かめられるの?
と気になるところだと思いますので、ここからは内部安定性の具体的な確かめ方をいくつか見ていきましょう。
極零相殺の有無による確かめ方
内部安定性は、不安定な極零相殺があるときに注意が必要なのでした。逆に言うと、内部安定性を確かめる鍵は不安定な極零相殺にあるとも言えます。
具体的には、次のようなフィードバック制御システムにおいて、不安定な極零相殺と内部安定性には、次のような関係があることが知られています。

- 不安定な極零相殺がなく、かつ閉ループ伝達関数が安定であれば、そのシステムは内部安定である。
- 不安定な極零相殺があるならば、(たとえ閉ループ伝達関数が安定でも)そのシステムは内部安定でない。
この関係を知っていれば、システムの内部安定性を手っ取り早くチェックできるので、頭に入れておくと便利です。
実用上、閉ループ伝達関数の安定性は必ず調べると思いますので、それに加えて不安定な極零相殺もチェックすればOK、と覚えておけばよいでしょう。
図式的な確かめ方
もう一つ、実用シーンでよく使われる確かめ方に、ナイキストの安定判別法が挙げられます。
ナイキストの安定判別法は、ベクトル軌跡を応用したナイキスト線図と呼ばれる図を用いて、フィードバック制御システムの内部安定性を図式的に判別する手法です。
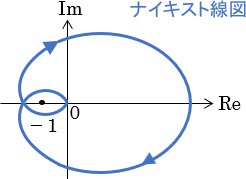
ナイキストの安定判別法の利点としては、「システムが内部安定かどうか」に加え、「安定な場合、それがどの程度安定であるのか」という安定余裕も分かる点が挙げられます。
※ナイキストの安定判別法については、こちらのページをご覧ください
数学的な確かめ方
実用シーンでは上述の確かめ方で事足りると思いますが、より理解を深めるために、内部安定性の数学的な条件についても確認しておきましょう。
内部安定性は、「システムに加わるすべての入力信号に対して、システム内のすべての信号が安定」であれば成り立つのでした。

よって、上図におけるそれぞれの信号の関係性(安定性)を地道に計算してみましょう。
今、システムの外から入力される信号は目標値$r$と外乱$d$ですので、次の安定性がそれぞれ成立すれば、このシステムは内部安定であることになります。
- $r$ から $y$ までの伝達関数 $G_{yr}(s)$ が安定
- $r$ から $u$ までの伝達関数 $G_{ur}(s)$ が安定
- $d$ から $y$ までの伝達関数 $G_{yd}(s)$ が安定
- $d$ から $u$ までの伝達関数 $G_{ud}(s)$ が安定
※$e$もシステムに含まれる信号ですが、個別に安定性を確かめる必要はありません。$e=r-y$なので、$y$が安定であれば自動的に$e$も安定になるためです。($r$は人が与えるものなので絶対に安定)
実際にそれぞれの伝達関数を導出してみましょう。
$$\begin{gather} r\ から\ y\ までの伝達関数\quad G_{yr}(s)={\frac{P(s)C(s)}{1+P(s)C(s)}} \\[3pt] r\ から\ u\ までの伝達関数\quad G_{ur}(s)={\frac{C(s)}{1+P(s)C(s)}}\\[3pt] d\ から\ y\ までの伝達関数\quad G_{yd}(s)={\frac{P(s)}{1+P(s)C(s)}}\\[3pt] d\ から\ u\ までの伝達関数\quad G_{ud}(s)={\frac{-P(s)C(s)}{1+P(s)C(s)}} \end{gather}$$
これらがすべて安定になる条件を、極から判定してみましょう。
システムの極は、「伝達関数の分母=0」として、それを$s$について解いたものでしたね。上記伝達関数の分母は全て同じであるので、次式を解くことで全ての極が導出できることになります。
$$1+P(s)C(s)=0$$
極と安定性の関係より、上式によって求めた極の実部が全て負であれば、上記伝達関数は全て安定であると言えます。よって、これこそが内部安定性の条件として利用できることになります。
ただし上式の計算時、$P(s)$と$C(s)$の間で極零相殺があっても約分せずに計算することに注意してください。約分すると不安定極が消えてしまい、安定性が正しく判定できなくなってしまいます。先ほどの極零相殺がある例で実際に計算してみると分かりやすいので、余裕があればやってみてくださいね。
まとめると、「$1+P(s)C(s)=0$(約分なし)によって求めた極の実部が全て負であれば、そのシステムは内部安定である」と抑えておけばよいでしょう。
※極と安定性の関係については、こちらのページをご覧ください
ちなみに、下図のようにシステムが検出器$H(s)$を持つ場合は、代わりに$1+P(s)C(s)H(s)=0$によって極を求めればOKです。(上と同じ計算で導出できます)
ただ、実際の所$1+P(s)C(s)=0$や$1+P(s)C(s)H(s)=0$は高次方程式となるため、手計算で解くのはかなり大変です。さらに、この方法では安定余裕までは求まらないため、実用性はナイキストの安定判別法が上と言えるでしょう。
※安定余裕の詳細については、こちらのページをご覧ください
以上、内部安定性とその判別方法についての解説でした!
- システムに加わるすべての入力信号に対して、システム内のすべての信号が発散しないならば、そのシステムは内部安定であるという
- 内部安定でなければ、システムは使い物にならない
- 不安定な極零相殺がなく、かつ閉ループ伝達関数が安定であれば、そのシステムは内部安定である
- 不安定な極零相殺があるならば、そのシステムは内部安定でない










コメント