このページでは、1次系(1次遅れ系・1次システム)の周波数特性とボード線図について、具体例を交えて詳しく解説します。また、1次系のよくある使い方についても解説します。
※周波数応答やボード線図の基礎を未学習の方は、まずこちらのページをご覧ください。
- 1次系は「信号の低周波成分はそのまま通し、高周波成分は周波数が高ければ高いほどカットする」という性質を持つ
- この性質を活かして、お手軽なローパスフィルタとして使える。
- 信号がカットされるかどうかの目安となる周波数は、$\frac{1}{T}$[rad/s](極の-1倍)
- この周波数は、システムの動作の速さの指標としても使える
1次系のボード線図
次の伝達関数で表される、1次系の周波数特性を考えましょう。
$$G(s)=\frac{1}{Ts+1}$$
※$T$は時定数です。1次系の数式表現や基本特性については、こちらのページをご覧ください
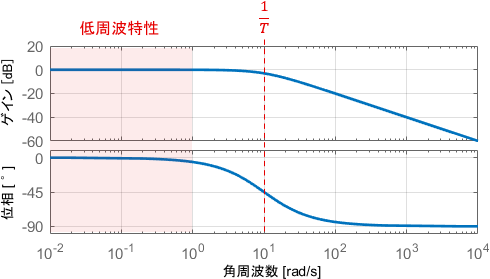
例えば$T=0.1$であるとき、システムのボード線図は次のようになります。
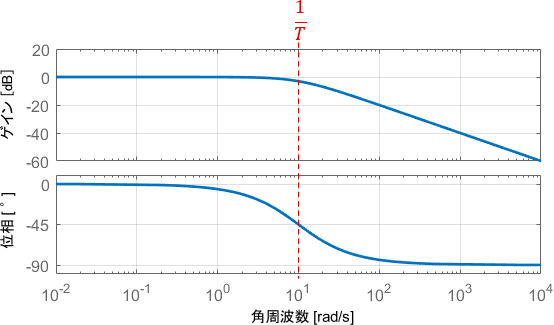

後で説明するように、このボード線図は数式から導出可能ですが、1次系のボード線図は非常によく使われるため、形をそのまま覚えてしまうことをオススメします。
ここからは、上図を例に1次系のボード線図を詳しく読み取っていきましょう。
※ちなみに$\frac{K}{Ts+1}$のように伝達関数に定数ゲイン$K$がかかる場合は、$K$と$\frac{1}{Ts+1}$を別々のシステムと見なし、それぞれのボード線図を足し合わせればOKです($K$は定数なので、結局ゲイン線図が$K$倍分上にずれるだけになります)。ボード線図の足し合わせの法則については、こちらのページをご覧ください。
ゲイン線図
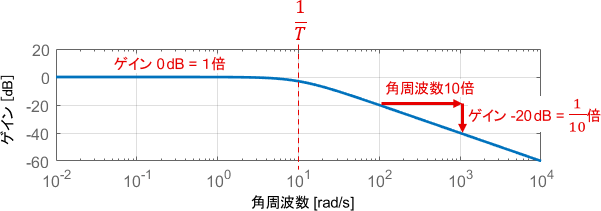

まずゲイン線図に注目すると、$\frac{1}{T}$より低い角周波数ではだいたいゲインが0dBとなっています。よって、角周波数が$\frac{1}{T}$以下の信号成分はそのままの大きさで出力される(システムをそのまま通過する)ことが分かります。
一方で$\frac{1}{T}$よりも高い角周波数では、角周波数が10倍になるごとに(つまり1decadeごとに)ゲインが20dBずつ小さくなっています。よって、角周波数が$\frac{1}{T}$以上の信号成分は周波数が高ければ高いほど減衰して出力される(カットされる)ことが分かります。
また、このように「1decadeごとに信号が-20dB分カットされる」という特性は、-20dB/decと表現されたりもします。
位相線図
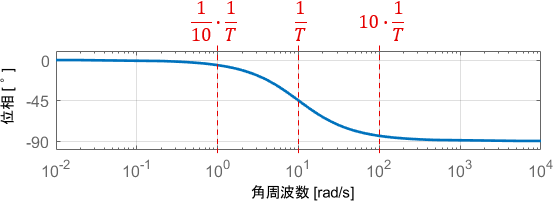

一方の位相線図からは、次の性質が読み取れます。
- $\frac{1}{10}\cdot\frac{1}{T}$以下では位相がだいたい0°(信号が遅れない)
- $\frac{1}{T}$では位相が-45°(信号が45°遅れる)
- $10 \cdot \frac{1}{T} $以上では位相がだいたい-90°(信号が90°遅れる)
ゲインと異なり、位相は角周波数がどれだけ高くなっても-90°で底打ちとなっていますね。
折れ曲がる角周波数の覚え方
以上のように、1次系は角周波数$\frac{1}{T}$を境にボード線図が折れ曲がり、周波数特性が大きく変化します。
この変化点である角周波数$\frac{1}{T}$はそのまま覚えてもよいですが、システムの極と対応させて覚えておくと便利です。具体的には、システムの極が$-\frac{1}{T}$なので、システムの極(の-1倍)がボード線図の折れ曲がり角周波数となると覚えておきましょう。
※当然角周波数は正である必要がありますが、基本的に周波数解析は安定なシステムを対象とするため、システムの極は負となります。よって、その-1倍(折れ曲がる角周波数)はしっかり正となってくれます。
※システムの極についてはこちらのページで解説していますので、合わせてご覧ください。
ボード線図の具体例と直感的イメージ
1次系の例:RC回路
ここからは、上で読み取ったボード線図の物理的な意味を考えることで、直感的イメージを深めていきましょう。
例として、次のRC回路を考えます。入力は電圧$v_{in}(t)$、出力は電圧$v_{out}(t)$です。
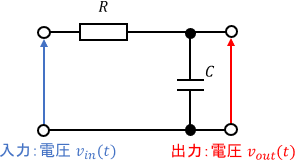

このシステムの伝達関数は、次のようになります。
$$G(s) = \frac{1}{RCs+1}$$
$RC=T$とすると、ちょうど先ほど考えた伝達関数$\frac{1}{Ts+1}$と同じ形となっていますね。以下、$T=0.1$の場合を例に、様々な周波数の入力信号に対する周波数特性を見ていきましょう。

※その他の1次系の例は、こちらの記事をご覧ください。具体的なシステムが何であれ、対象が1次系であれば、その直感的イメージは以下の説明と同じです。
低周波特性のイメージ
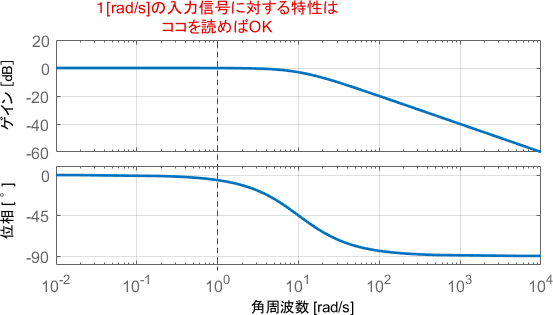
まず、そこそこ遅い入力電圧$v_{in}(t)$として、1[rad/s]のsin波を与えてみましょう。この入力信号に対する特性は、ボード線図の1[rad/s]の部分を読み取れば分かります。

このときの入出力信号の、具体的な波形を見てみましょう。
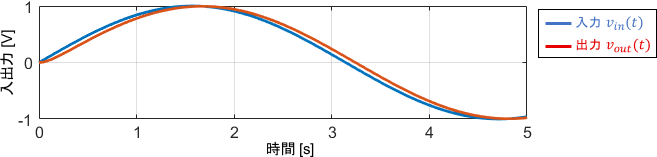

入力信号が少しだけ遅れて出力されているような挙動が得られていますね。ボード線図と照らし合わせて、この挙動を読み取ってみましょう。
まずゲイン線図に注目すると、ゲインは0dB(つまり1倍)となっています。出力信号の振幅を見ると、確かに入力信号の振幅と変わっていませんね。
一方で位相線図に注目すると、位相には少しだけ遅れが生じています。この作用により、入力に対して出力が少し遅れているわけです。
ちなみに、さらに低周波の信号を入れるとゲイン・位相ともに0になるため、入力信号がそのまま出力されるような挙動となります。
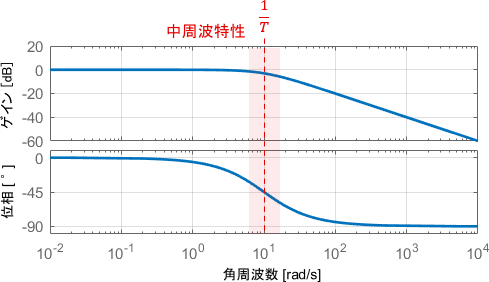
中周波特性のイメージ
次に、入力電圧$v_{in}(t)$として10[rad/s]のsin波を与えた場合について考えましょう。この入力信号に対する特性は、ボード線図の10[rad/s]の部分を読み取れば分かりますね。
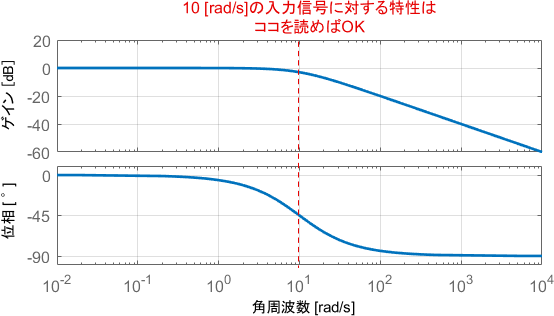

このときの入出力信号の、具体的な波形を見てみましょう。
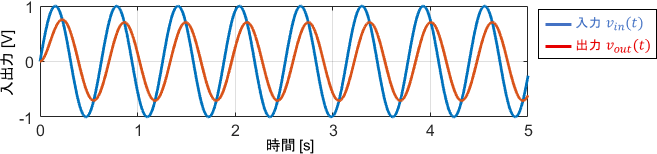

入力に対して、出力がついていけなくなっている感じの挙動が得られていますね。ボード線図と照らし合わせて、この挙動を読み取ってみましょう。
まずゲイン線図に注目すると、ゲインは数dBマイナスとなっています。出力信号の振幅を見ると、確かに入力信号に対して振幅が少し小さくなっていることが見て取れます。
一方で位相線図に注目すると、位相が45°(sin波$\frac{1}{8}$個分)遅れていることが分かります。出力信号を見ると、確かにそれだけ遅れていますね。
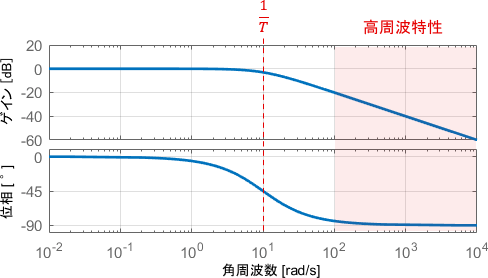
高周波特性のイメージ
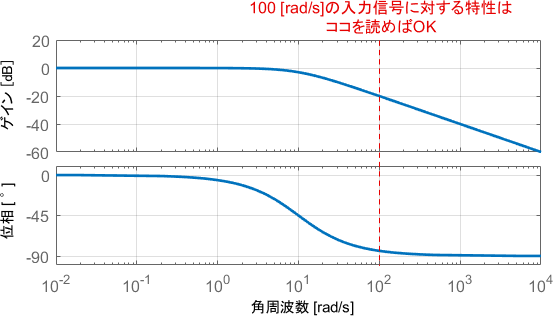
最後に、そこそこ速い入力電圧$v_{in}(t)$として、100[rad/s]のsin波を与えた場合について考えましょう。この入力信号に対する特性は、ボード線図の100[rad/s]の部分を読み取れば分かります。

このときの入出力信号の、具体的な波形を見てみましょう。
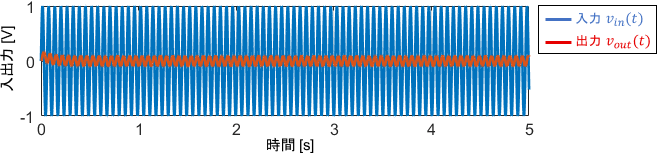

…いかにも反応できていない感じの挙動ですね。ボード線図と照らし合わせて、この挙動を読み取ってみましょう。
まずゲイン線図に注目すると、ゲインは-20dB(つまり0.1倍)となっています。出力信号の振幅を見ると、確かに入力信号の0.1倍ほどに小さくなっていますね。
位相線図に注目すると、位相がだいたい90°(sin波$\frac{1}{4}$個分)遅れていることが分かります。出力波形をよーく見ると確かにそれだけ遅れていることが確認できます。
ちなみに、さらに高周波の信号を入れるとゲインが超小さくなるため、入力信号が消えてしまうような挙動となります。角周波数がどんなに高くなっても位相は-90°のままですが、そもそも信号がほぼなくなってしまうため、位相はほとんど意味をなさなくなります。
以上の3つの例より、1次系は「ボード線図が折れ曲がる角周波数(=極の-1倍)」を目安に出力信号が入力信号についていけなくなることが分かります。逆に言うと、この折れ曲がり角周波数を指標として、システムの動作の速さを判断することができます。例えば、折れ曲がり角周波数が高ければ高いほどより速い入力信号についていけるので、「システムの動作は速い」と判断できるわけですね。
1次系の使い方(周波数特性の観点で)
次に、周波数特性の観点で見た、1次系のよくある使い方について解説していきましょう。
※こちらのページでは、インパルス応答・ステップ応答の観点から1次系の使い方を解説していますので、合わせてご覧ください。
上で確認したとおり、1次系は「信号の低周波成分はそのまま通し、高周波成分は周波数が高ければ高いほどカットする」という特性を持ちます。これを活かして、お手軽なローパスフィルタとして使われることが多いです。
例えば先ほどのRC回路は、それがそのまま高周波の電圧信号をカットするローパスフィルタとして使用できます。高周波信号(考慮したい周波数以上の信号)はほぼノイズであり、それを除去するために1次系を利用できるというわけです。
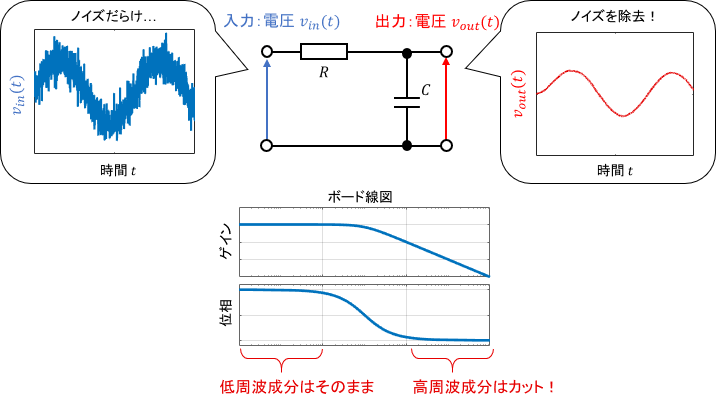

このRC回路、抵抗とコンデンサをつなぐだけなので非常にお手軽ですよね。複雑な配線や外部電源は必要ありません。
さらに、信号をカットし始める周波数$\frac{1}{T}$(ボード線図が折れ曲がる周波数)は抵抗値$R$とコンデンサの容量$C$によって調整できるので、設計もお手軽です。($T=RC$でしたね)
もちろん上記のような電気システム以外でも、1次系は同様にフィルタとして作用します。1次系を意図的にフィルタとして実装する場合はもちろん、意図せず1次系が含まれる場合でも、それが結果的にローパスフィルタとして作用することを覚えておくとよいでしょう。
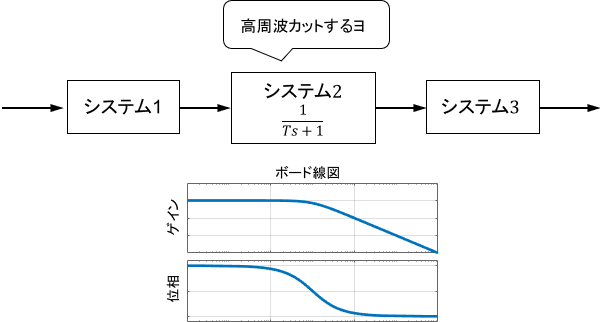

周波数伝達関数からボード線図を導出(参考)
最後に、1次系のボード線図を数式から導出してみましょう。まず、周波数伝達関数から周波数特性を計算し、それが確かにボード線図と一致することを確認していきます。
※前述の通り、1次系のボード線図はその形を丸々覚えてしまえば実用上はほとんど困らないので、この節は読み飛ばしても大丈夫です。当然、数式を理解していればシステムへの理解も深まるので、余裕があれば学習してみてください。
システムの周波数特性は、周波数伝達関数$G(j\omega)$から計算できるのでした($j$は虚数単位、$\omega$は角周波数)。具体的には、$G(j\omega)$をベクトルとして複素平面上にプロットしたとき、その絶対値$|G(j\omega)|$がゲイン、偏角$\angle G(j\omega)$が位相となります。
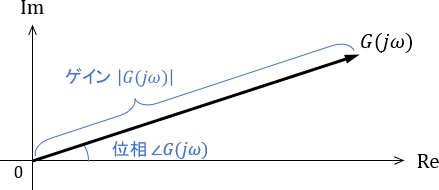

ここからは、次に示す1次系の周波数伝達関数$G(\omega j)$を用いて、周波数特性を計算していきましょう。
$$G(\omega j)=\frac{1}{T\omega j+1}$$
※周波数伝達関数についてはこちらのページで詳しく解説していますので、合わせてご覧ください。
低周波特性
まず、考慮する角周波数$\omega$が折れ曲がり角周波数$\frac{1}{T}$よりも大幅に低い場合を考えます。このとき、$\omega$と$T$の間には次の関係が成り立ちます。
$$\begin{align} &\omega \ll \frac{1}{T} \quad より、\\[5pt] &T\omega \ll 1 \end{align}$$
$T\omega$が1よりも大幅に小さいのでこの部分を無視すると、周波数伝達関数は次のように近似できます。
$$G(\omega j)=\frac{1}{\ubg{T\omega j}{無視}+1}\approx 1$$
伝達関数が1ということは、「入力がそのまま出力される」ということですね。これを複素平面上にベクトルとしてプロットし、ゲインと位相を導出してみましょう。
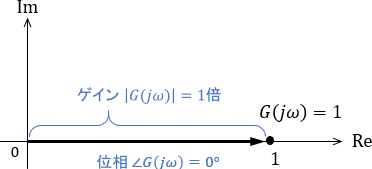

低周波信号に対する特性は、ゲインが1倍(つまり0dB)、位相が0°であると導出できました。確かにボード線図と一致していますね。

中周波特性
続いて、考慮する角周波数$\omega$が折れ曲がり角周波数$\frac{1}{T}$に等しい場合を考えます。このとき、$\omega$と$T$の間には次の関係が成り立ちます。
$$\begin{align} &\omega =\frac{1}{T} \quad より、\\[5pt] &T\omega = 1 \end{align}$$
この関係を用いると、周波数伝達関数は次のように計算できます。
$$\begin{align}G(\omega j)&=\frac{1}{T\omega j+1} = \frac{1}{ j+1} \\[5pt] &= \frac{j-1}{(j+1)(j-1)}= \frac{1}{2} – \frac{1}{2}j\end{align}$$
これを複素平面上にベクトルとしてプロットし、ゲインと位相を導出してみましょう。
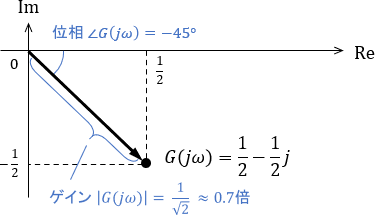

中周波信号に対する特性は、ゲインが約0.7倍(つまり-数dB)、位相が-45°であると導出できました。これもボード線図と一致しています。

高周波特性
最後に、考慮する角周波数$\omega$が折れ曲がり角周波数$\frac{1}{T}$よりも大幅に高い場合を考えます。このとき、$\omega$と$T$の間には次の関係が成り立ちます。
$$\begin{align} &\frac{1}{T} \ll \omega \quad より、\\[5pt] & 1 \ll T\omega \end{align}$$
$T\omega$が1よりも大幅に大きいので1を無視すると、周波数伝達関数は次のように近似できます。
$$G(\omega j)=\frac{1}{T\omega j+\ubg{1}{無視}}\approx \frac{1}{T\omega j}=- \frac{1}{T\omega}j$$
これを複素平面上にベクトルとしてプロットし、ゲインと位相を導出してみましょう。


信号の角周波数$\omega$に応じて、ゲイン$|G(j\omega)|=\frac{1}{T\omega}$が変化する結果となりました。具体的には、角周波数$\omega$が10倍になるごとに、ゲインは$\frac{1}{10}$倍(つまり-20dB)となります。確かにゲイン線図の傾向と一致していますね。
一方、ベクトルの向きは角周波数$\omega$によらず絶対に下方向なので、位相は-90°で固定となります。

以上、1次系の周波数特性とボード線図についての解説でした。
- 1次系は「信号の低周波成分はそのまま通し、高周波成分は周波数が高ければ高いほどカットする」という性質を持つ
- この性質を活かして、お手軽なローパスフィルタとして使える。
- 信号がカットされるかどうかの目安となる周波数は、$\frac{1}{T}$[rad/s](極の-1倍)
- この周波数は、システムの動作の速さの指標としても使える









コメント