このページでは、積分要素(積分器)の周波数特性とボード線図について、詳細を解説します。また、積分要素を用いる際の実用上のポイントついても解説します。
※周波数応答やボード線図の基礎を未学習の方は、まずこちらのページをご覧ください。
- 積分要素は「信号の低周波成分は増幅させ、高周波成分は減衰させる」という性質を持つ
- システムの定常特性を改善するために付加されることが多い
- ただし、システムに積分要素を付加すればするほど安定性に悪影響が出るので注意が必要
積分要素の基本
本題に移る前に、基礎をおさらいしておきましょう。積分要素(積分器)は、$\frac{1}{s}$で表されるシンプルな要素ですね。
これ単体で1つのシステムを構成するというよりも、システムの一部として登場することがほとんどでしょう。

※積分要素単体で表されるシステムの例については、こちらのページをご覧ください。
積分要素が他の要素と組み合わさったとき、具体的にどのような作用を及ぼすのかを見てみましょう。ある信号$f(t)$(そのラプラス変換は$F(s)$)に積分要素$\frac{1}{s}$を作用させたときの影響は、次のように求められます。
$$F(s) \cdot \frac{1}{s} \xrightarrow{\large 逆ラプラス変換} \int ^t _0 f(\tau) d\tau $$
「積分要素」という名前の通り、対象を積分する作用をしていますね。
積分範囲は、0から$t$(考慮している時刻)までです。制御の場合、時刻0は制御開始時刻、$t$は制御中の現在時刻となることがほとんどですので、「制御開始時刻から現在時刻まで」とイメージすればOKです。積分範囲は意外と忘れがちなので、しっかり抑えておきましょう。
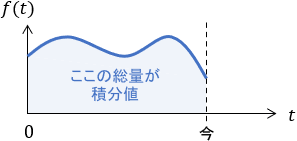
※ちなみに、ステップ入力(ステップ関数)も$\frac{1}{s}$で表されますが、これは「インパルス応答(つまり1)を積分したもの」と解釈すればOKです。詳細はこちらのページで解説していますので、合わせてご覧ください。
積分要素のボード線図
それでは、積分要素$\frac{1}{s}$のボード線図を確認していきましょう。
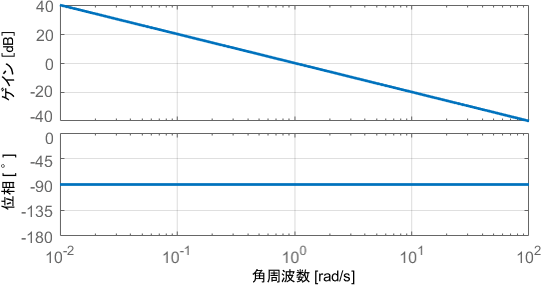
このボード線図は伝達関数から導出可能ですが、実用上非常によく使われるものなので、形をそのまま覚えてしまうことをオススメします。
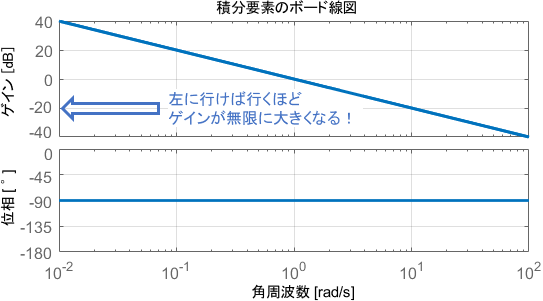
まずゲイン線図に注目すると、角周波数が10倍になるごとに(つまり1decadeごとに)ゲインが20dBずつ小さくなる直線になっていますね。つまり、信号の低周波成分は増幅させ、高周波成分は減衰させる特性が読み取れます。
また、角周波数が1[rad/s]のときに、増幅・減衰の境目となる0dB(1倍)になることも覚えておきましょう。
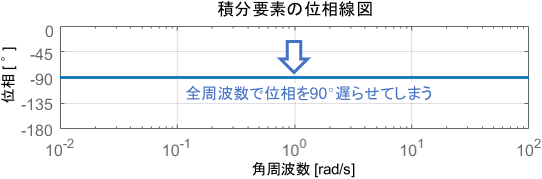
一方の位相線図は、角周波数によらず常に-90°ですね。つまり、周波数によらずどの信号も90°遅れることが読み取れます。
※$\frac{K}{s}$のように積分要素に定数$K$がかかる場合は、$K$と$\frac{1}{s}$を別々のシステムと見なし、それぞれのボード線図を足し合わせればOKです($K$は定数なので、結局ゲイン線図が$K$倍分上にずれるだけになります)。ボード線図の足し合わせの法則については、こちらのページをご覧ください。
ボード線図の具体例と直感的イメージ
ここからは、上で読み取ったボード線図の意味を具体例で確認することで、直感的イメージを深めていきましょう。
下図のように、シンプルな積分要素$G(s)=\frac{1}{s}$に対し、様々な角周波数$\omega$の入力信号$u(t)=\sin (\omega t)$を与え、それに対する周波数応答$y(t)$を確認していきます。
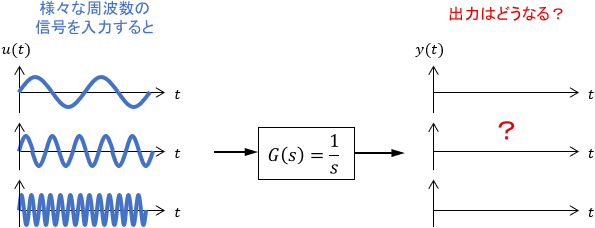
低周波特性のイメージ
まず、そこそこ遅い入力信号として0.5[rad/s]のsin波を与えた場合について考えます。この入力信号に対する特性は、ボード線図の0.5[rad/s]の部分を読み取れば分かりますね。
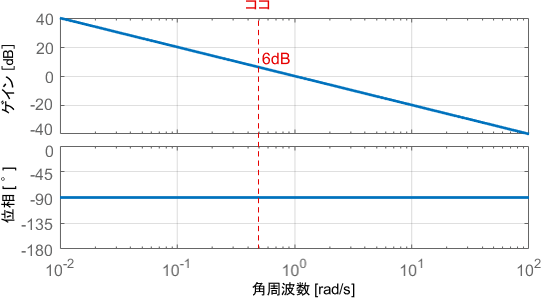
このときのゲインの値は6dB、位相の値は-90°です。入出力信号の具体的な波形を見てみましょう。
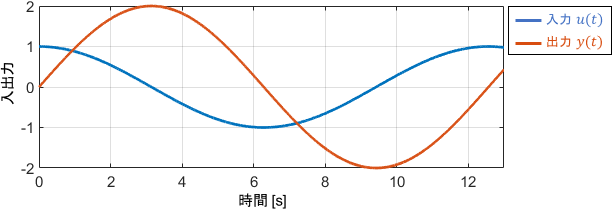
まず信号の振幅に注目すると、入力信号が増幅されて出力されていることが見て取れます。その倍率は6dB(約2倍)であり、ゲイン線図の内容と一致していますね。
一方で位相に注目すると、入力信号が90°(つまりsin波$\frac{1}{4}$個分)遅れて出力されていることが見て取れます。信号のピークの位置を比べると分かりやすいですね。これも位相線図の内容と一致しています。
また、信号波形から、出力信号が確かに入力信号の積分値になっていることも見て取れますね。
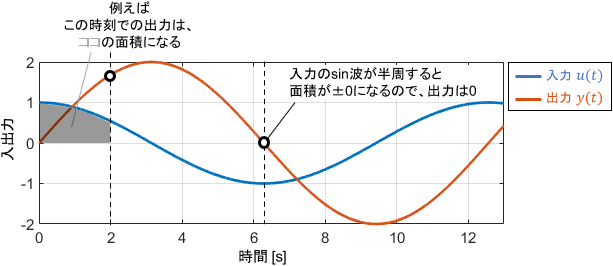
入力信号の周波数が低いのでsin波ひとヤマ分の面積が大きくなり、積分値である出力信号が入力より大きくなっていることが直感的にも分かります。この作用により、入力信号が増幅されているような挙動が現れるというわけですね。
中周波特性のイメージ
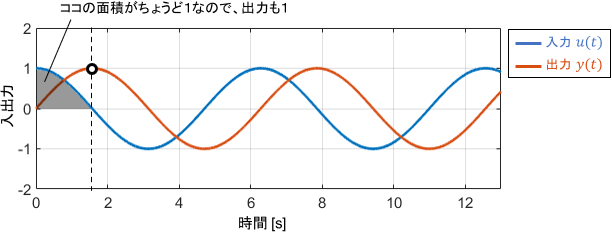
続いて、入力信号として1[rad/s]のsin波を与えた場合について考えましょう。この入力信号に対する特性は、ボード線図の1[rad/s]の部分を読み取れば分かります。
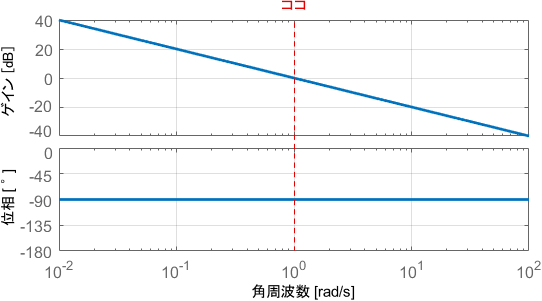
このときのゲインの値は0dB、位相の値は-90°です。入出力信号の具体的な波形を見てみましょう。
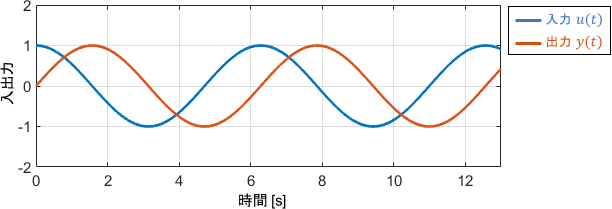
まず、信号の振幅が変わっていないことが見て取れますね。つまり増幅率0dB(1倍)であり、ゲイン線図の内容と一致していることが分かります。
信号の位相を見ると、入力信号が90°(つまりsin波$\frac{1}{4}$個分)遅れて出力されていることが見て取れます。これも位相線図に一致しますね。
積分関係に着目すると、この周波数にて入力のsin波ひとヤマ分の面積がちょうど1になるため、入出力信号の振幅が一致していると解釈できます。
高周波特性のイメージ
最後に、そこそこ速い入力信号として2[rad/s]のsin波を与えた場合について考えましょう。この入力信号に対する特性は、ボード線図の2[rad/s]の部分を読み取れば分かります。
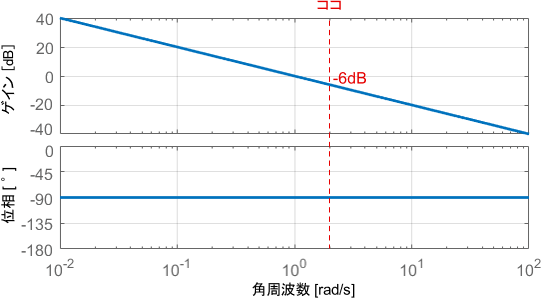
このときのゲインの値は-6dB、位相の値は-90°です。入出力信号の具体的な波形を見てみましょう。
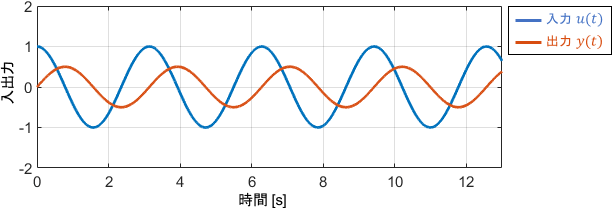
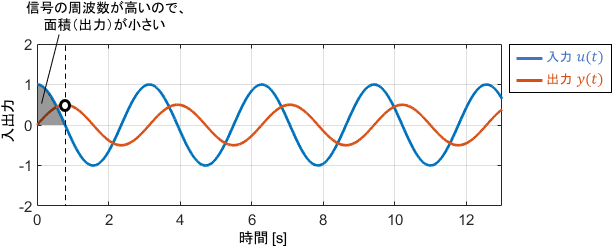
信号の振幅に注目すると、今度は入力信号が小さくなって出力されていることが分かりますね。その倍率は-6dB(約1/2倍)であり、ゲイン線図の値と一致しています。
位相は変わらず90°遅れており、しっかり位相線図に一致しています。
積分関係に着目すると、入力信号の周波数が高いのでsin波ひとヤマ分の面積が小さくなり、積分値である出力信号が入力より小さくなっていることが直感的に理解できます。
実用上のポイントと使い方
※ここから先は少し応用的な内容となるため、初めて学習する方は流し読みでも構いません。
積分要素と定常特性
積分要素は、システムの定常特性を改善するためによく使われます。
特に内部モデル原理は、積分要素がキーとなる代表的な法則と言えるでしょう。内部モデル原理は、「開ループ伝達関数が目標値と同じ数の積分要素を持っていれば、定常偏差が0になる」といったものでしたね。
※内部モデル原理の詳細については、こちらのページで詳しく解説しています。
基本的な理屈は上記ページを参照いただくとして、ここでは「なぜ内部モデル原理では積分要素がキーになるのか」について、ボード線図の観点から解釈してみましょう。
まずこちらのページにて、「ボード線図を極限まで左に行った領域は定常特性を表すこと」そして「その領域で、開ループシステムのゲインが大きければ大きいほど定常特性がよくなること」を説明しました。
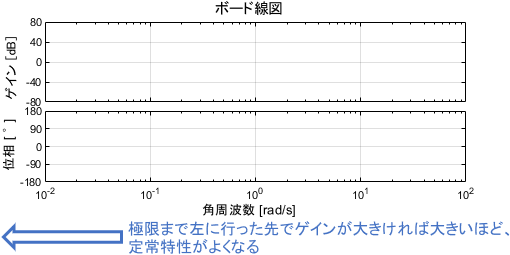
積分要素のボード線図は、上で確認したとおり「左に行けば行くほどゲインが無限に大きくなる」という形をしていましたね。これはまさに上記の条件を満たしており、積分要素は定常特性の改善にうってつけであることが分かります。
積分要素と安定性
一方で、積分要素を用いる場合には安定性への影響に注意する必要があります。
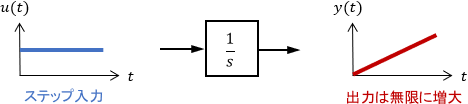
まず積分要素の極は0なので、積分要素単体は安定なシステムではありません。積分要素にステップ入力を与え続けると、それが積分されることで出力は発散してしまいますよね。
※システムの安定性、および極と安定性の関係性については、こちらのページをご覧ください。
積分要素を既存のシステムに付加する場合も、安定性に悪影響を及ぼすので注意が必要です。
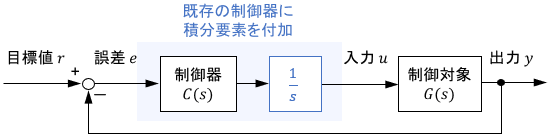
この理由を安定余裕の観点から見ていきましょう。
※安定余裕の詳細については、こちらのページをご覧ください
安定余裕に関してまず着目すべきは、位相余裕です。位相余裕は「開ループシステムのボード線図において、ゲイン交差周波数での位相が-180°より進めば進むほど、システムの安定性が増す」というものでした。よってゲイン交差周波数での位相はなるべく-180°より上にあることが望ましいと言えます。
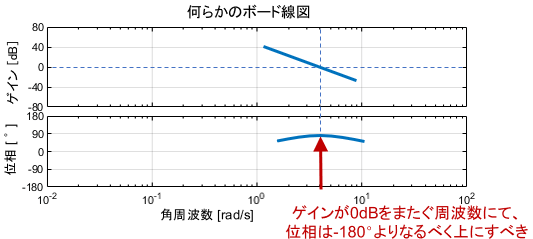
対して積分要素は、全周波数で位相を90°遅らせてしまう特性を持っていました。
よって、積分要素を既存のシステムに1つ付加するたび位相が90°ずつ遅れてしまい、システムの位相余裕が減少することになります。
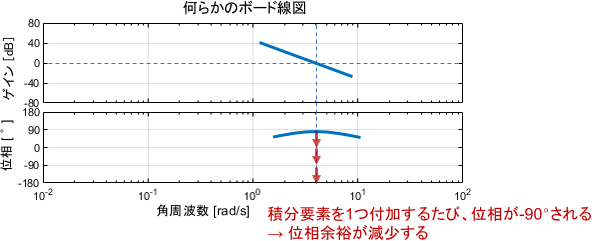
もし付加したことでゲイン交差周波数での位相が-180°を下回ると、システムは不安定になり使えなくなってしまうため、注意が必要です。
位相余裕の観点では、90°の位相遅れというのは結構大きなものです。もともとの位相余裕が大きなシステムに対しては積分要素を多数つけることも可能ですが、実用上は積分要素は2個以下しか使えないことがほとんどでしょう。通常は0個、それだと望む性能が得られないなら1個、どうしても必要な特別な理由があれば2個、といったイメージを持っていればよいかと思います。
また、積分要素を付加することで、ゲイン線図も変化することに注意してください。積分要素のゲイン線図は右肩下がりの直線でした。よってこれを既存のシステムに付加すると、ちょうどゲイン線図を時計回りに回転させるような作用をすることになります。

だいたいの場合は、これによってシステムのゲイン交差周波数(位相余裕を考えるべき周波数)がずれることになるので、それも考慮に入れて安定余裕を評価する必要があります。
積分要素の欠点を低減する方法
基本の考え方
ここからは、制御器に積分要素を含める必要が出た際に、上記のような悪影響を低減する方法について紹介します。
定常特性の改善に積分要素が有用なのは、「低周波領域にてゲインが無限に大きくなるから」でしたね。逆に言うと、(定常特性の観点では)積分要素の性質は低周波領域以外では特に必要なく、むしろ安定性に悪影響を与えるので無くしたほうがよいと言えるでしょう。
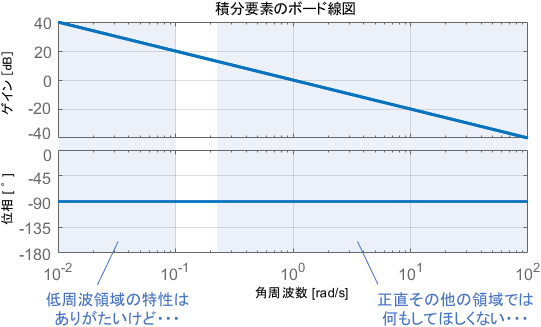
そこで、「低周波領域では積分要素と同じように働き、その他の領域では何もしない要素」を考えることにします。
代表例
これを実現するための方法は様々ありますが、簡単な例として次のものが挙げられます。
$$G(s)=\frac{K_1s+K_2}{s}$$
$K_1,K_2$は定数です。例として、$K_1 = K_2 = 1$としたときのボード線図を見てみましょう。
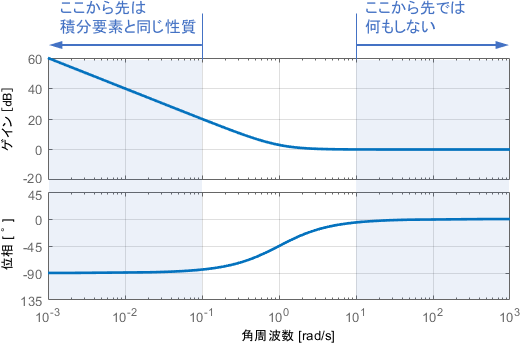
低周波領域の性質は積分要素と同じで、それが高周波領域に行くに連れてゲインが0dB、位相が0°に向かっていますね。
ゲイン0dB、位相0°は「入力信号に何もせずそのまま出力する」ということなので、まさにこれが「低周波領域では積分要素と同じように働き、その他の領域では何もしない要素」であると解釈できます。性能が切り替わる周波数は、$K_1,K_2$の値で調整可能というわけですね。
実は、実用シーンでよく用いられるPI制御器は、まさにこの形をしています。
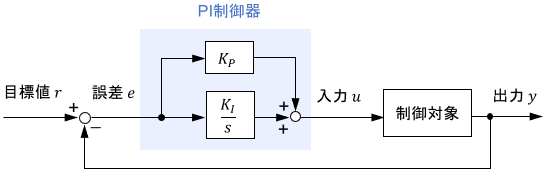
$K_P,K_I$は定数の制御ゲインです。制御器部分を通分すると、確かに上記と同じ形になっていることが分かります。
$$PI制御器:K_P + \frac{K_I}{s} = \frac{K_Ps+K_I}{s}$$
この作用により、PI制御器はシンプルながらそこそこ良好な制御性能が得られるというわけですね。
※PI制御を含めた、PID系の制御については、こちらのページをご覧ください
ボード線図の導出
ちなみに上で示したボード線図は、次のように考えることで導出できます。ボード線図の理解が深まりますので、余裕があれば抑えておいて下さい。
まず、伝達関数を次の2つに分割して考えます。
$$G(s)= \ubg{(K_1s+K_2)\vphantom{\frac{1}{s}}}{G_1(s)} \cdot \ubg{\frac{1}{s}}{G_2(s)}$$
そしてそれぞれのボード線図を足し合わせましょう。$G_1(s)$は1次系$\frac{1}{K_1s+K_2}$のボード線図の上下反転を考えればOKです。$G_2(s)$は積分要素そのままですね。$K_1 = K_2 = 1$の場合を下図に示します。
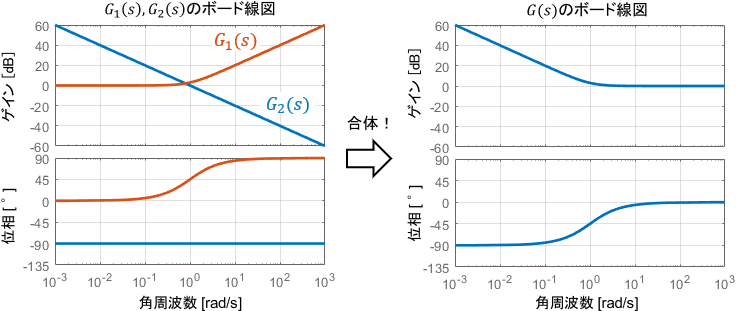
10[rad/s]以上の領域では、積分要素$G_2(s)$の性質が$G_1(s)$によって綺麗に打ち消されていることが分かりますね。
※ここで用いた、ボード線図の足し合わせ・上下反転の法則については、こちらのページをご覧ください。
以上、積分要素の周波数特性・ボード線図・実用上のポイントについての解説でした。
- 積分要素は「信号の低周波成分は増幅させ、高周波成分は減衰させる」という性質を持つ
- システムの定常特性を改善するために付加されることが多い
- ただし、システムに積分要素を付加すればするほど安定性に悪影響が出るので注意が必要














コメント