このページでは、ベクトル軌跡(ベクトル線図)の読み方・書き方・利点について、直感的イメージを踏まえて分かりやすく解説します。また、基本的なシステムのベクトル軌跡の例についても詳しく紹介します。
- 入力信号の周波数$\omega$を0から∞まで変化させたときに、周波数伝達関数$G(j\omega)$が複素平面上に描く軌跡のことをベクトル軌跡と呼ぶ
- 全体的な使いやすさはボード線図に劣るのが欠点
- ナイキストの安定判別法に応用することで、フィードバック制御システムの安定性を図式的に判別できるのが利点
- 実用上は、ナイキストの安定判別法に使われることがほとんど
ベクトル軌跡とは
ベクトル軌跡は、システムの周波数特性を表現する図の一種です。
※「ベクトル軌跡が描かれた図」という意味で「ベクトル線図」と呼ばれることもあります
周波数特性とは、「システムに様々な周波数のsin波を入力したとき、出力されるsin波の振幅と位相がどのように変化するか」を表すものでしたね。
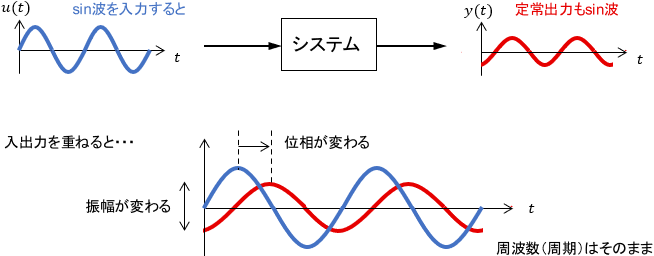
あるシステム$G(s)$の周波数特性を求めるには、そのシステムの周波数伝達関数$G(j\omega)$を考えればよいのでした($\omega$は入力信号の角周波数、$j$は虚数単位です)。
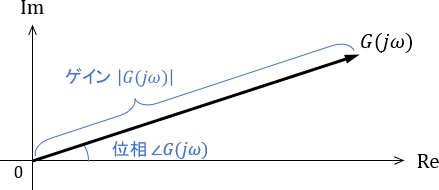
より具体的には、周波数伝達関数$G(j\omega)$を複素平面上にプロットしたとき、ベクトル$G(j\omega)$と周波数特性には、次の関係性があるのでしたね。
- ベクトルの絶対値$|G(j\omega)|$は、ゲインに等しい(振幅が何倍になるか)
- ベクトルの偏角 $\angle G(j\omega)$は、位相に等しい(位相が何度ずれるか)
※周波数特性・周波数伝達関数の詳細については、こちらのページをご覧ください
ベクトル$G(j\omega)$は角周波数$\omega$の関数なので、$\omega$に応じて様々に変化します。周波数特性は「様々な入力周波数$\omega$に対する出力の特性」であったので、入力周波数$\omega$を様々に変化させたときのベクトル$G(j\omega)$の様子を見てみることにしましょう。
適当なシステムに対してやってみた結果がこちらです。
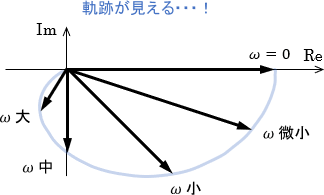
入力周波数$\omega$が変化するに連れてベクトルが指す位置が変化し、軌跡を描いていることが分かりますね。これがベクトル軌跡です。
より厳密には、入力信号の角周波数$\omega$を0から∞まで変化させたときに、周波数伝達関数$G(j\omega)$が複素平面上に描く軌跡のことをベクトル軌跡と呼びます。
※角周波数$\omega$が出てきましたが、これは周波数[Hz]の単位を変えたものなので、本質的には信号の周波数(速さ)を表すものと思えばOKです。詳細は、こちらのページをご覧ください。
ベクトル軌跡の書き方
それでは、ベクトル軌跡の書き方(ルール)について、より詳しく見ていきましょう。
ベクトル軌跡の書き方は、次のようにまとめられます。
- 角周波数$\omega$を0から∞まで変化させながら、周波数伝達関数$G(j\omega)$を複素平面上に描く
- 軌跡上の代表的な点に、角周波数$\omega$の値を記入する。
- 角周波数が大きくなる方向に矢印をつける
例題を通じて、それぞれの工程を具体的に見ていきましょう。次のような、1次系のベクトル軌跡を描いてみることにします($T$は時定数です)。
$$G(s)=\frac{1}{Ts+1}$$
手順1:周波数伝達関数を複素平面上に描く
まずは上記手順通り、角周波数$\omega$を0から∞まで変化させながら、周波数伝達関数$G(j\omega)$を複素平面上に描いていきましょう。
描きやすいように、周波数伝達関数を実部と虚部に分けて整理しておきます。
$$\begin{align}G(j\omega) &= \frac{1}{T\omega j+1} = \frac{1}{T\omega j+1}\cdot \frac{T\omega j-1}{T\omega j-1}\\[5pt] &= \ubg{\frac{1}{(T\omega)^2+1}}{実部(横軸座標)}\ \ubg{- \frac{T\omega}{(T\omega)^2+1}}{虚部(縦軸座標)}j\end{align}$$
これに様々な$\omega$を代入して、複素平面上に$G(j\omega)$をプロットしてみましょう。
このとき、周波数伝達関数の実部・虚部がキリのいい値になる$\omega$を選ぶのがコツです。特に、実部・虚部が0になるときに軌跡が縦軸・横軸と交わるため、これらを抑えておくと軌跡の概形がつかみやすくなります。
$$\begin{array}{lllll} T\omega = 0 & つまり&\omega = 0&のとき、&G(j\omega)=1 \\ T\omega = \frac{1}{\sqrt{3}} & つまり&\omega = \frac{1}{\sqrt{3}T}&のとき、&G(j\omega)=\frac{3}{4} – \frac{\sqrt{3}}{4}j \\T\omega = 1 & つまり&\omega = \frac{1}{T}&のとき、&G(j\omega)=\frac{1}{2} – \frac{1}{2}j \\ T\omega = \sqrt{3} & つまり&\omega = \frac{\sqrt{3}}{T}&のとき、&G(j\omega)=\frac{1}{4} – \frac{\sqrt{3}}{4}j \\ T\omega = \infty & つまり&\omega = \infty&のとき、&G(j\omega)=0\end{array}$$
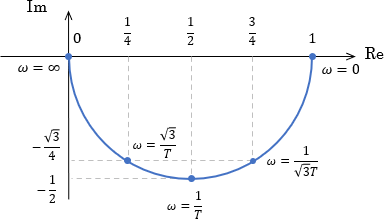
ちょうど半径$\frac{1}{2}$の半円状の軌道になりましたね。上記以外の$\omega$を代入してみても、$G(j\omega)$は必ずこの軌道上に位置するので、余裕があれば確かめてみてください。
※ちなみに、上記のように地道に$\omega$を代入する方法の他に、一度システムのボード線図を描き、それを元にベクトル軌跡を描く方法もあります。それについてはページの最後で簡単に紹介していますので、参考にしてください。
手順2:軌跡上の代表的な点に角周波数の値を記入する
次は、代表点と角周波数の記入です。
代表点の選び方に特にルールはありませんが、$\omega=0$の点、$\omega=\infty$の点、実軸・虚軸との接点、軌跡の極値点が選ばれることが多いです。
今回の場合は$\omega=0$、$\omega=\frac{1}{T}$、$\omega=\infty$がそれらに当たりますが、せっかく求めたので、その他の点も全部入れておきましょう。
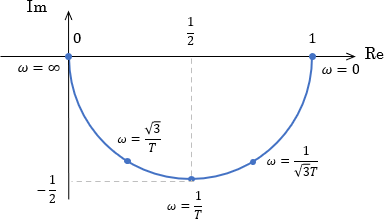
手順3:角周波数が大きくなる方向に矢印をつける
後は最後の仕上げとして、角周波数が大きくなる方向に矢印をつければベクトル軌跡の完成です。
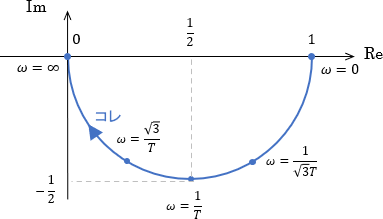
※角周波数$\omega$の値を見れば大きくなる方向は分かるので、矢印をつけない流派もあります。
ベクトル軌跡の読み方

頑張って書いてみたはいいけど・・・いまいちピンとこないな。
ベクトル軌跡はどんなイメージで読んだらいいの?
と思いますよね。これまでの説明でベクトル軌跡のルールは分かったと思いますので、ここからは読み方のイメージを説明していきましょう。
基本の読み方
読み方の基本は、冒頭に説明した周波数伝達関数とゲイン・位相の関係です。

ベクトル軌跡上で周波数伝達関数$G(j\omega)$の絶対値$|G(j\omega)|$と偏角$\angle G(j\omega)$を読み取れば、それがその角周波数でのゲインと位相、すなわち周波数特性になるというわけです。
例えば先ほど描いた1次系$G(s)=\frac{1}{Ts+1}$の$\omega=\frac{1}{\sqrt{3}T}$での周波数特性は、下図のように読み取ることができます。
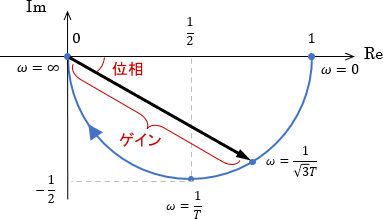
上図の場合、$G(j\omega)$が1よりも小さい絶対値(ゲイン)を持つため、入力信号が減衰して出力されることが分かります。また、$G(j\omega)$が実軸に対してマイナス方向の偏角(位相)を持つため、信号の位相が遅れて出力されることも分かります。
ここからは、ベクトル軌跡におけるゲインと位相の読み方について、それぞれの直感的なイメージを説明していきましょう。
ゲインのイメージ
ゲインは結局、「周波数伝達関数$G(j\omega)$が指す場所の原点からの距離」で表されますよね。これより、$G(j\omega)$とゲインの間には次の関係性が成り立つことが分かります。
- 原点を中心とした半径1の円上:ゲインが1なので、入力信号の大きさが変わらず出力される
- 原点を中心とした半径1の円内:ゲインが1以下なので、入力信号が減衰して出力される
- 原点を中心とした半径1の円外:ゲインが1以上なので、入力信号が増幅して出力される
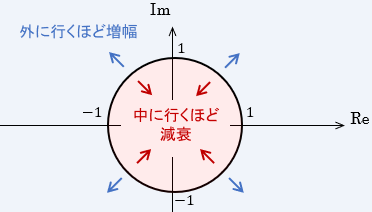
よって対象とするベクトル軌跡が上記のどのエリアにあるかを見れば、信号の増幅/減衰はすぐに読み取れることになります。
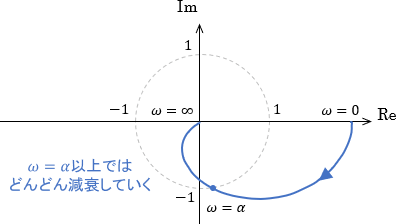
さらにこのイメージを拡張すると、システムが定数倍された場合、そのベクトル軌跡は原点を中心にその倍率だけ拡大(or縮小)されることも分かります。
例えば、先ほどの1次系$G(s)=\frac{1}{Ts+1}$に定数ゲイン $K=\frac{1}{2}$ や $K=2$ をかけた$G'(s)=\frac{K}{Ts+1}$のベクトル軌跡は、次のようになります。

位相のイメージ
続いては位相です。位相は結局「周波数伝達関数$G(j\omega)$が指す場所の実軸に対する角度」で表されるため、下図のようなイメージを持てばよいことになります。
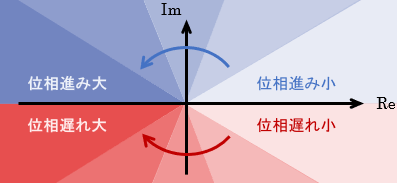
超ざっくり言うと、「左側のエリアに行けば行くほど位相のズレが大きくなる(よくない)」と思っておけばOKです。
代表点以外の周波数
上記イメージを持ちながら、いざベクトル軌跡を読んでみると、こんな状態になりがちです。

あれ、読みたい角周波数が軌跡上に書いてないぞ?
代表点では角周波数が書いてあるけど、それ以外の角周波数はどう読んだらいいんだ!?
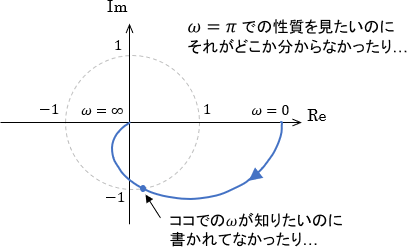
結論から言うと、ベクトル軌跡のみを手がかりに$\omega$の値が書いていない場所での角周波数を正確に読み取ることは不可能なので、諦めるしかありません。(他の角周波数との位置関係からある程度推測することは可能ですが)

よって、ベクトル軌跡は特定の角周波数での性質を正確に読み取るものではなく、周波数特性の全体的な傾向を読み取るものであると理解しておきましょう。
ベクトル軌跡の利点・欠点・使い方

えっ、書かれてない角周波数が分からないって、メチャクチャ不便なんじゃないの?
ボード線図はそんなことはなかったし、ボード線図使ったほうがいいんじゃないの?
正直その通りです。
「システムの周波数特性を見る」という用途であれば、同じく周波数特性を表す図であるボード線図のほうが優れています。
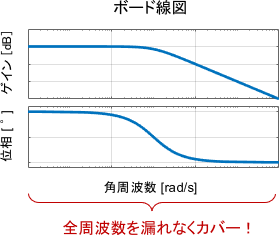
ボード線図であれば、全ての周波数に対するゲインと位相を漏れなく読み取れますし、実用的な便利法則がたくさんありますからね。
※ボード線図の詳細については、こちらのページをご覧ください

・・・では、ベクトル軌跡の存在意義とは
実用上、ベクトル軌跡はナイキストの安定判別法に使われることがほとんどです。ナイキストの安定判別法は、ベクトル軌跡を応用したナイキスト線図によって、下図のようなフィードバック制御システムの安定性を図式的に判別する方法です。
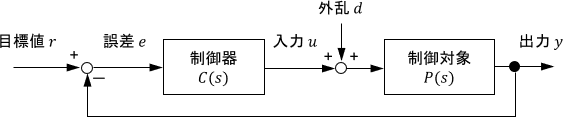
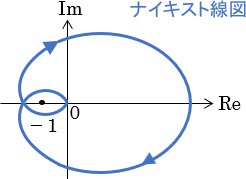
フィードバック制御システムの安定性は「内部安定性」という観点で考える必要があるため、数式から安定性を判別しようとすると計算がかなり面倒になってしまいます。ナイキストの安定判別法では、それを図によって視覚的に判断できるため、実用性に優れていると言えます。
※内部安定性とナイキストの安定判別法については、こちらのページをご覧ください
以上より、ベクトル軌跡の欠点・利点・使い方は、次のようにまとめられます。
- 欠点:個別の角周波数での特性を読み取れないので、ボード線図より使いにくい。
- 利点:ナイキストの安定判別法に応用することで、フィードバック制御システムの安定性を図式的に判別できる
- 使い方:実用上は、ナイキストの安定判別法に使われることがほとんど
基本システムのベクトル軌跡例
最後に、基本的なシステムのベクトル軌跡を確認して、ベクトル軌跡に慣れておきましょう。
先ほどやったように、周波数伝達関数$G(j\omega)$に様々な角周波数$\omega$を代入して軌跡を確認してもよいのですが、基本システムはその周波数特性(ボード線図)がよく知られているので、ボード線図と見比べながら下図の関係性に基づいて軌跡を確認していくことにします。

1次系のベクトル軌跡
まずは、先ほども描いた1次系のベクトル軌跡を、ボード線図と見比べながら確認しましょう。
$$G(s)=\frac{1}{Ts+1}$$

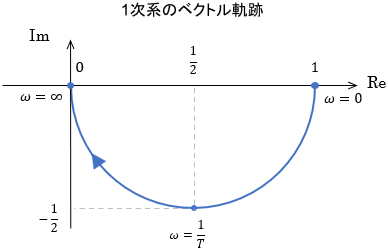
※1次系のボード線図の詳細については、こちらのページをご覧ください
※伝達関数に定数ゲイン$K$がかかって$G(s)=\frac{K}{Ts+1}$となっている場合は、上で説明したように、ベクトル軌跡全体を原点を中心に$K$倍拡大/縮小すればOKです(他のシステムでも同様です)
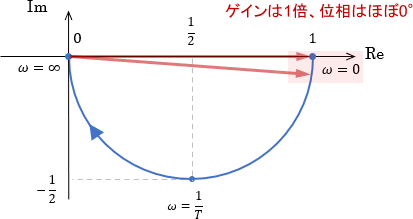
低周波領域
まず、低周波領域に注目しましょう。ボード線図を見ると、ゲインはずっと1倍(0dB)ですね。位相はほぼ0°ですが、右端のエリアでは少し遅れが生じています。
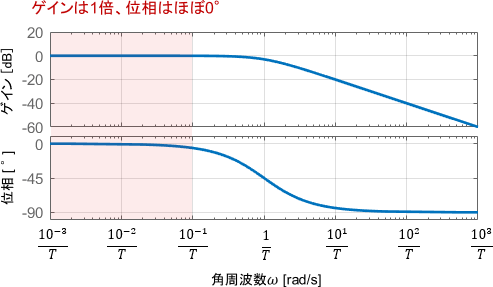
ベクトル軌跡にてこの領域を見ると、確かにボード線図の内容と一致していることが分かります。
中周波領域
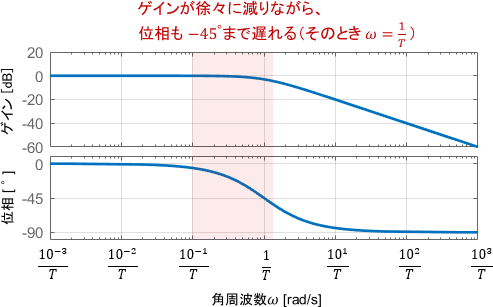
続いて、もう少し周波数の高い領域に注目しましょう。ボード線図を見ると、ゲインは最初1倍(0dB)ですが、周波数が高くなるにつれて徐々に減少していることが分かります。位相はどんどん遅れ、角周波数$\omega=\frac{1}{T}$にて-45°になっていますね。
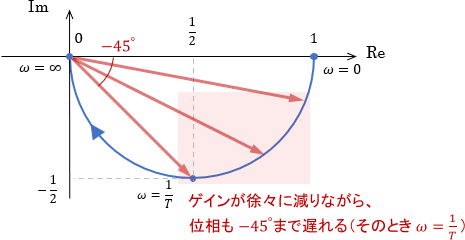
ベクトル軌跡にてこの領域を見ると、確かにそのようになっていますね。
高周波領域
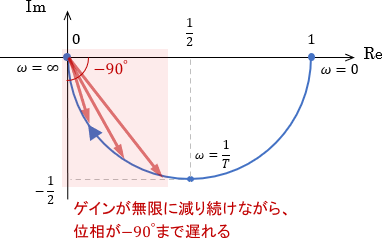
最後に高周波領域です。ボード線図より、ゲインは無限に減り続ける一方、位相は-90°まで遅れることが分かります。
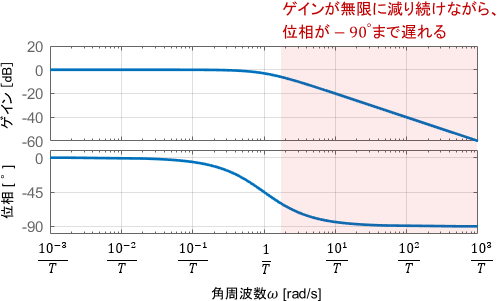
ベクトル軌跡の高周波領域を見ると、確かにそのようになっていることが分かります。
2次系のベクトル軌跡
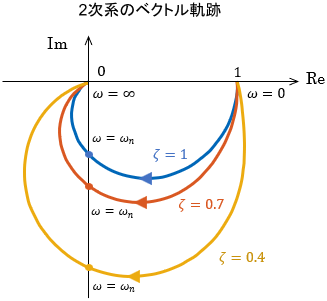
続いて、次式で表される2次系のベクトル軌跡を確認していきましょう。
$$G(s)=\frac{\omega _n ^2}{s^2 + 2\zeta \omega _n s + \omega _n ^2}$$
$\zeta$は減衰係数、$\omega_n$は固有角周波数です。2次系の性質は減衰係数$\zeta$の値によって変化するため、いくつかの$\zeta$のものをまとめて見ていきましょう。
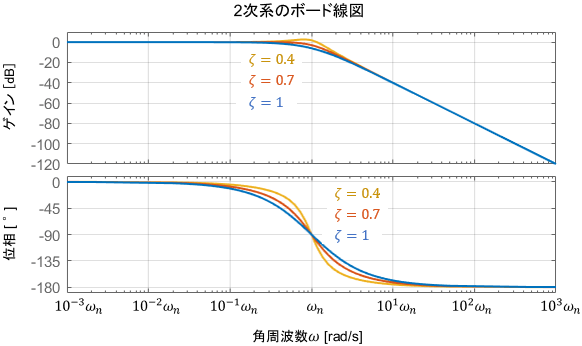
※2次系のボード線図の詳細については、こちらのページをご覧ください
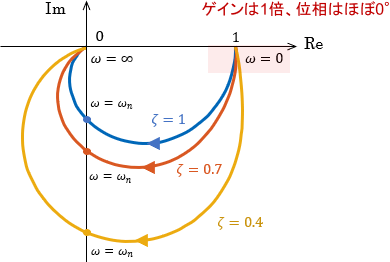
低周波領域
まずは、低周波領域です。ボード線図を見ると、ゲインはずっと1倍(0dB)となっていますね。位相はほぼ0°ですが、右端のエリアでは少し遅れが生じています。1次系の場合と同じ傾向ですね。
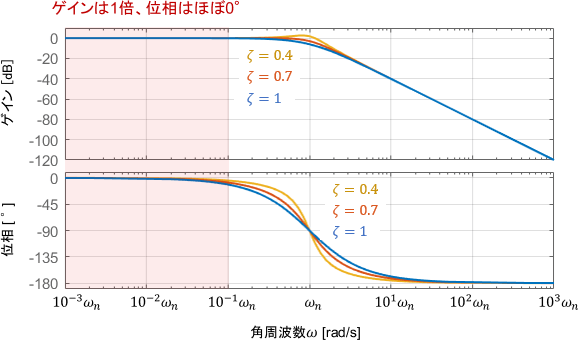
ベクトル軌跡にも、同様の傾向が見られます。
中周波領域
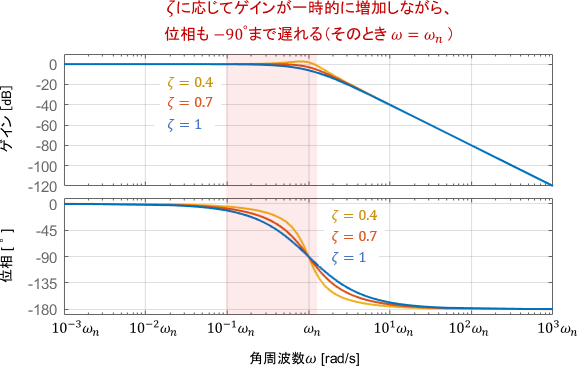
もう少し高い周波数に注目していきましょう。
ボード線図を見ると、ゲインは最初1倍(0dB)ですが、$\zeta$の値が小さいほどそれが一時的に増加し、最終的には減少に転じていることが見て取れます。$\zeta=1$ と $\zeta=0.4$ を比較すると、違いが分かりやすいですね。
一方の位相はどんどん遅れ、角周波数$\omega=\omega _n$にて-90°になっています。
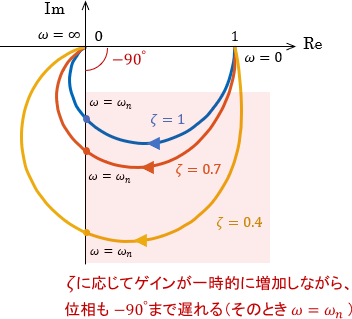
ベクトル軌跡も、確かにボード線図の傾向に一致しています。$\zeta$が小さいほどゲインの一時的な増加が大きくなるため、下方向に大きく膨らんだ軌跡となっていますね。
高周波領域
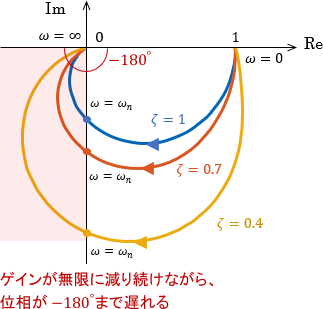
最後に高周波領域です。ボード線図より、ゲインは無限に減り続ける一方、位相は-180°まで遅れることが分かります。

ベクトル軌跡にも、その傾向が現れていますね。最終位相が-180°なので、軌道がグルっと回り込むような形で原点に収束しています。
積分要素のベクトル軌跡
最後は、次式で表される積分要素のベクトル軌跡です。
$$G(s)=\frac{1}{s}$$
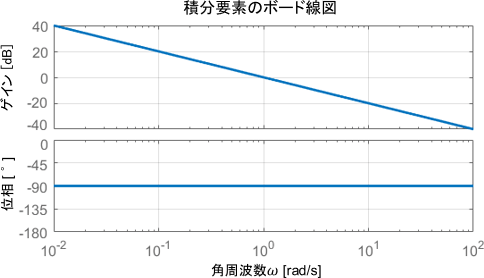
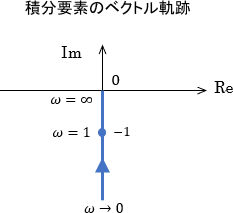
※積分要素のボード線図の詳細については、こちらのページをご覧ください
積分要素はシンプルなので、結構分かりやすいです。ゲインに注目すると$\omega=1$では1倍(0dB)で、それ以下の周波数では無限に増加、それ以上の周波数では無限に減少し続けています。一方の位相は-90°で一定ですね。
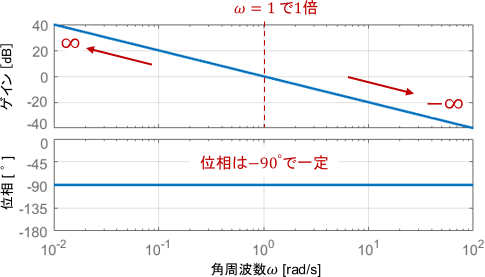
ベクトル軌跡を見ると、確かにそのようになっています。$\omega=0$では軌跡は無限の彼方にあり、それが原点に一直線に向かっているイメージです。
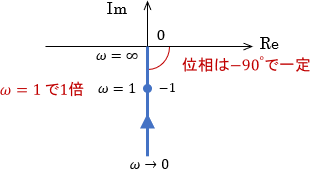
以上3つの基本システムを紹介してきましたが、同様に考えることで基本システム以外のベクトル軌跡も、ボード線図を経由して描くことが可能です。次のように一度システムのボード線図を描き、それを元にベクトル軌跡を描くわけですね。
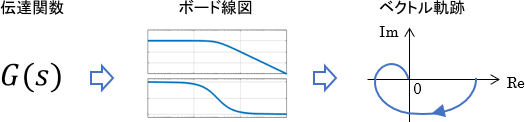
特に、対象システムが複雑な場合は、地道に$\omega$を代入してベクトル軌跡を描こうとすると計算がかなり面倒になります。一方、ボード線図は様々な便利法則を駆使することで、複雑なシステムでもある程度簡単に描くことが可能です。
システムに応じて、ケースバイケースで描き方を選ぶのがベストだと言えるでしょう。
※ボード線図の便利法則とそれを使った描き方については、こちらのページをご覧ください
以上、ベクトル軌跡の読み方・書き方・利点についての解説でした。
- 入力信号の周波数$\omega$を0から∞まで変化させたときに、周波数伝達関数$G(j\omega)$が複素平面上に描く軌跡のことをベクトル軌跡と呼ぶ
- 全体的な使いやすさはボード線図に劣るのが欠点
- ナイキストの安定判別法に応用することで、フィードバック制御システムの安定性を図式的に判別できるのが利点
- 実用上は、ナイキストの安定判別法に使われることがほとんど












コメント