ナイキストの安定判別法では、開ループ伝達関数のベクトル軌跡上の点(-1,0)が安定/不安定の境目として重要な役割を持っていました。
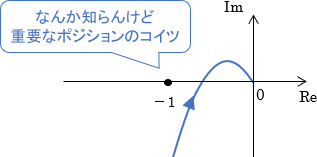
このページでは、点(-1,0)で結局何が起きているのかを見ながら、ナイキストの安定判別法の直感的イメージを解説します。
※ナイキストの安定判別法について未学習の方は、まずこちらのページをご覧ください。本ページでは、こちらのページで紹介した「簡易版ナイキストの安定判別法」に基づいて解説を進めていきます。
- 点(-1,0)を境に、信号がフィードバックループをグルグル回る際の挙動が変わる
- 点(-1,0)では、信号がフィードバックループを永遠に回り続けるので、安定限界になる
- 点(-1,0)より少し右にズレた点では、信号がループを回るたびに減衰されるので、安定になる
- 点(-1,0)より少し左にズレた点では、信号がループを回るたびに増幅されるので、不安定になる
点(-1,0)の意味
まずは、そもそも点(-1,0)が何を表しているのかを復習しましょう。
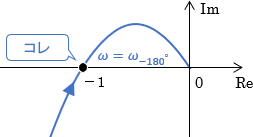
ベクトル軌跡における点(-1,0)は、ゲイン1倍・位相-180°を表します。
より具体的には、「その点の角周波数(上図でいう$\omega = \omega_{-180^\circ}$)の信号を入力すると、出力の大きさは1倍で変わらず、位相は180°遅れる」というシステムの性質を表しているわけですね。
※ベクトル軌跡の読み方については、こちらのページをご覧ください
ちなみに、この「位相が-180°となる周波数$\omega_{-180^\circ}$」は、位相交差周波数と呼ばれます。位相交差周波数は、ちょうどベクトル軌跡が実軸(横軸)と交わる点での周波数を表しているわけですね。
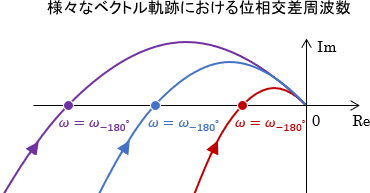
また、ナイキストの安定判別法で用いるのは、開ループ伝達関数のベクトル軌跡でしたので、上記は開ループシステムの性質を表していることも思い出しておきましょう。

以上を踏まえて、ここからは点(-1,0)前後での信号の変化を実際に確かめていきましょう。
具体的には、開ループ伝達関数のベクトル軌跡がそれぞれ下図のように表されるシステムに対して、位相交差周波数$\omega_{-180^\circ}$の信号を入力し、出力信号が具体的にどうなるのかを確認していきます。
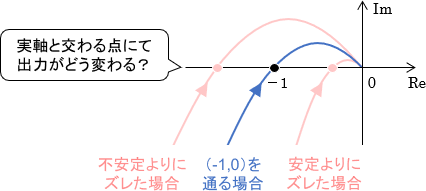
点(-1,0)での信号の様子
最初の例として、開ループ伝達関数$C(s)P(s)$のベクトル軌跡が点(-1,0)を通る、次のシステムを考えます。
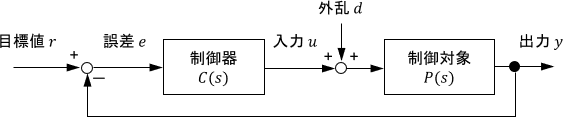
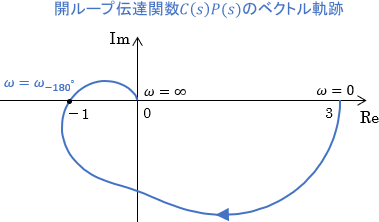
開ループシステムでの信号の様子を確認
点(-1,0)での信号の様子を直接確認するために、開ループシステムに位相交差周波数$\omega_{-180^\circ}$のsin波を入力してみましょう。
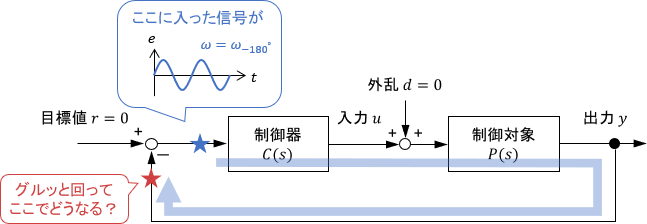
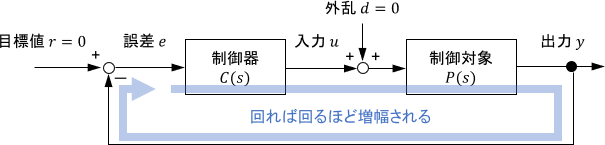
なお、問題をシンプルにするため、上図のように目標値$r$と外乱$d$は0とし、純粋に信号がフィードバックループをグルッと回った際の信号を確認することにします。(以降の例でも同じです)
得られた結果がこちらです。
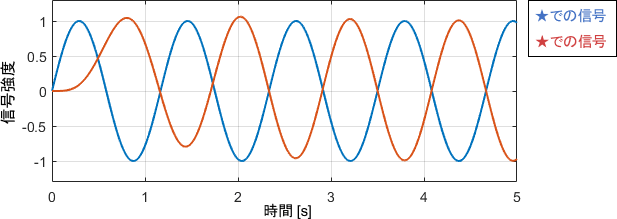
定常状態での入出力の関係に注目しましょう。
まず、出力の振幅は入力と等しいため、ゲインが1倍であることが分かります。また、出力の位相は入力に対して半周期分遅れているので、位相が-180°であることも分かりますね。これは、点(-1,0)が表す性質に確かに一致しています。
さらに少しだけループを進め、信号が最初のスタート地点に帰ってきたときにどうなっているのかも見てみましょう。
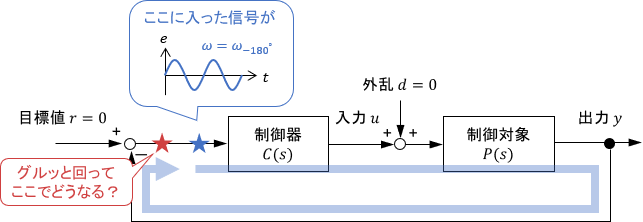

$r-y$を見ているわけですが、目標値$r=0$なので、先ほどの出力信号の上下反転である$-y$が得られています。見ての通り、定常状態では入出力が一致していますね。この意味で、点(-1,0)は特別と言えるわけです。
グルッと回って信号が全く変わらないということは、信号はそのループを永遠に回り続けるということになりますよね。
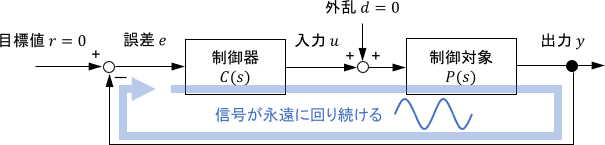
信号は発散こそしませんが、永遠に振動が収まらない安定限界にあることになるので、ここが安定/不安定の境目になっていると言えます。
閉ループシステムでの信号の様子を確認
安定限界にある状態をより直感的に把握するために、同じシステムの閉ループ特性も見てみましょう。
先ほどのシステムに対し、ステップ状の目標値を与えた際の出力の様子を確認してみます。
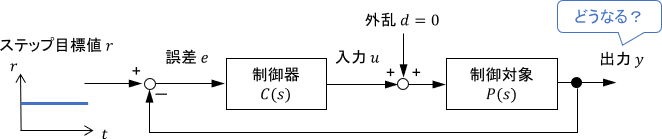
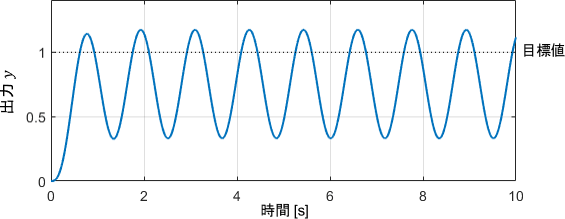
システムが安定限界にあるため、確かに閉ループシステムの出力も振動し続けていることが分かりますね。
少し安定よりにズレたときの信号の様子
ベクトル軌跡が点(-1,0)を通ると安定限界になることは分かったので、今度は軌跡が下図のように少し安定より(右側)にズレたシステムにて、信号の様子を確認してみましょう。
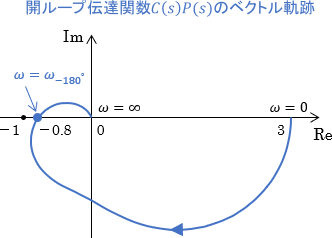
開ループシステムでの信号の様子を確認
まずは先ほど同様に、開ループシステムに位相交差周波数$\omega_{-180^\circ}$のsin波を入力し、信号がフィードバックループをグルッと回った際の様子を確認してみます。

ベクトル軌跡より、位相交差周波数$\omega_{-180^\circ}$での開ループシステムの特性は、ゲインが0.8倍・位相が-180°であることが分かります。先ほどの例よりゲインが小さくなっていますね。
実際に得られた信号波形がこちらです。
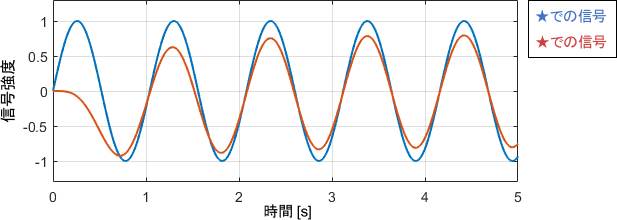
ベクトル軌跡から読み取った性質の通り、定常状態では入力信号がゲインの数(0.8倍)だけ減衰して出力されていますね。
ということは、ループを回れば回るほど信号はどんどん減衰し、最終的には無くなることになります。
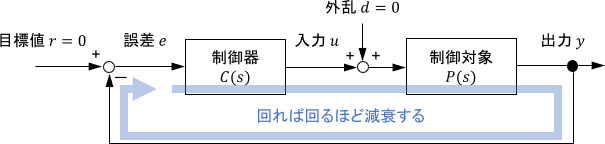
ほっといても信号が収束するため、システムは安定であることが分かりますね。
閉ループシステムでの信号の様子を確認
より直感的に理解するために、同じシステムの閉ループ特性も見てみましょう。
先ほどのシステムに対し、ステップ状の目標値を与えた際の出力の様子を確認してみます。

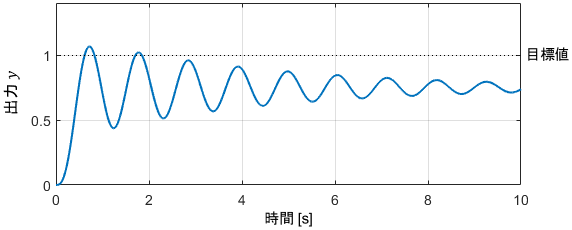
システムが安定であるため、閉ループシステムの出力もある値に収束していることが分かりますね。
目標値に収束できていないため制御性能に改善の余地はありますが、今はシステムの安定性を議論しているため、特に深掘りせず次に行きたいと思います。
※ちなみにこの場合、開ループ伝達関数に積分要素を持たせると、出力が目標値に収束するようになります。詳細については、こちらのページをご覧ください
少し不安定よりにズレたときの信号の様子
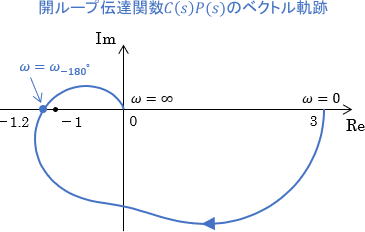
最後に、開ループ伝達関数のベクトル軌跡が下図のように少し不安定より(左側)にズレたシステムについても、同様に確認してみます。
開ループシステムでの信号の様子を確認
まずは開ループシステムに位相交差周波数$\omega_{-180^\circ}$のsin波を入力し、信号がフィードバックループをグルッと回った際の様子を確認しましょう。

ベクトル軌跡より、位相交差周波数$\omega_{-180^\circ}$での開ループシステムの特性は、ゲインが1.2倍・位相が-180°であることが分かります。
実際に得られた信号波形がこちらです。
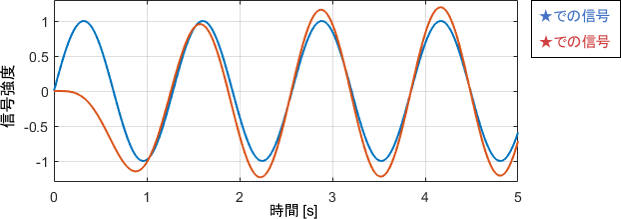
ベクトル軌跡から読み取った性質の通り、定常状態では入力信号がゲインの数(1.2倍)だけ増幅されて出力されていますね。
ということは、ループを回れば回るほど信号はどんどん増幅され、最終的には発散することになります。
ほっといたら信号が発散するので、システムは不安定であると言えます。
閉ループシステムでの信号の様子を確認
より直感的に理解するために、同じシステムの閉ループ特性も見てみましょう。
先ほどのシステムに対し、ステップ状の目標値を与えた際の出力の様子がこちらです。

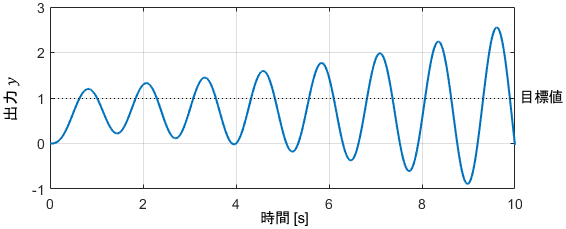
システムが不安定であるため、閉ループシステムの出力が発散してしまっていることが分かりますね。
以上、ナイキストの安定判別法の直感的イメージについての解説でした!
点(-1,0)を境に信号がフィードバックループをグルグル回る際の挙動が変わり、結果的にシステムの安定性が決定づけられているわけですね!
- 点(-1,0)を境に、信号がフィードバックループをグルグル回る際の挙動が変わる
- 点(-1,0)では、信号がフィードバックループを永遠に回り続けるので、安定限界になる
- 点(-1,0)より少し右にズレた点では、信号がループを回るたびに減衰されるので、安定になる
- 点(-1,0)より少し左にズレた点では、信号がループを回るたびに増幅されるので、不安定になる






コメント
いつも勉強させていただいております。ありがとうございます。
質問があります。
「開ループシステムでの信号の様子を確認」の最初に、サイン波を入力するとあり、かつ、このサイン波がブロック線図の制御器の直前の状態として示されています。ただし、制御器に入力されるのは目標値とフィードバック値の差の誤差であるため、制御器への初期の入力値はr=0ではないでしょうか?
それとも、初期の誤差としてサイン波を想定していて、制御器に入力しているということでしょうか?
イメージとしては後者の解釈のほうが近いです。
「開ループシステムを考える」ということは、「C(s)P(s)に対する入出力関係を考える」ということに対応します。つまり、「閉ループシステムがフィードバック制御を行っている最中のある信号を考える」のではなく、単純に「C(s)P(s)にsin波を入力した際の出力を確認する」と考えればOKです。これによって「sin波がループを一周回るとどう変化するのか」を見ていることになります。
※「さらに少しだけループを進め、信号が最初のスタート地点に帰ってきたとき」については、「-C(s)P(s)に対する入出力関係を考えている」と解釈すればOKです。