PID制御にあまり詳しくない人がPIDチューニングについて調べた際、最初に遭遇するであろう「それらしい方法」が限界感度法です。ただし、限界感度法はあまりアテにしすぎてはいけない方法です。
このページでは、限界感度法の概要と、その利点・欠点・使い所について解説します。限界感度法についての知識を深め、効果的に活用していきましょう!
- 限界感度法は、簡単でお手軽であるのが最大の利点
- 性能が悪く、安全性に注意が必要なのが欠点
- 基本的には限界感度法を使わず、手作業でチューニングしたほうがよい結果が得られる
- 緊急時の最後の手段や、参考情報としては使える
※PID制御の基礎を未学習の方は、まずこちらのページをご覧ください。
限界感度法とは
限界感度法は、PIDゲインをチューニングする方法の1つです。まずは、その方法について順番に説明していきましょう。
問題設定
次のPID制御システムを考えます。
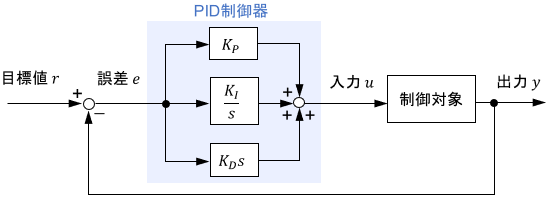

$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Pの項} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{Iの項} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Dの項}$$
限界感度法では、表現を完結にするために上式を次のように変形します。
$$u(t) = K_P \biggr(\ubg{ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Pの項} + \ubg{\frac{1}{T_I} \int ^t _0 e(\tau) d\tau}{Iの項} + \ubg{T_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Dの項}\biggl)$$
ここで、$T_I=\frac{K_P}{K_I}$は積分時間、 $T_D=\frac{K_D}{K_P}$は微分時間と呼ばれる定数です。調整パラメータは$K_P,K_I,K_D$から$K_P,T_I,T_D$に変わりましたが、表現を変えただけで本質的には何も変わっていないことに注意してください。
※ちなみに、PID制御器をこのように変形することは、限界感度法に限らずよくあります。$K_P$によって制御入力全体の大きさを簡単に調整できるためです。
限界感度法の手順
まず、Pの項以外の係数を0に設定し、P制御(比例制御)のみを有効化します。
$$u(t) = \ubg{K_P\ e(t)}{Pの項のみ} $$
この状態でシステムに一定の目標値(ステップ目標値)を与え、Pゲインを小さな値から徐々に大きくしていきます。すると、出力の振動の振幅がだんだんと大きくなっていきます。
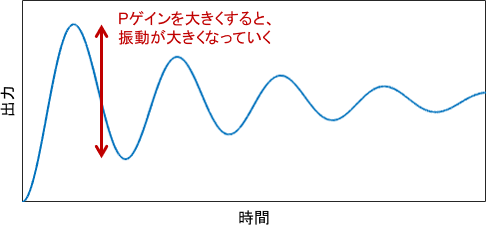

引き続きPゲインを大きくしていくと、ある時点で振動が減衰しなくなり、持続振動を形成するようになります。出力が収束しないので、この状態は不安定状態の入り口、つまり安定限界であると解釈できます。
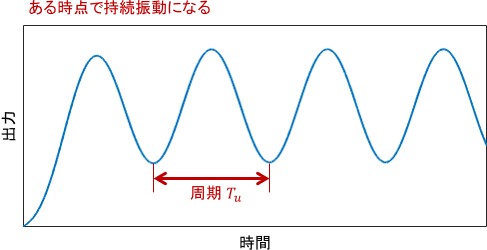

このときのPゲイン$K_{u}$と、持続振動の周期$T_u$を基準に、PIDゲインを次のように設定するのが限界感度法です。
| 使う制御 | $K_P$ | $T_I=\frac{K_P}{K_I}$ | $T_D=\frac{K_D}{K_P}$ |
|---|---|---|---|
| P制御 | $0.5K_{u}$ | – | – |
| PI制御 | $ 0.45K_{u}$ | $0.83T_u$ | – |
| PID制御 | $0.6K_{u}$ | $0.5T_u$ | $0.125T_u$ |
限界感度法がこのようになっている背景思想(仕組み)について、簡単に解説しておきましょう。
まずPゲイン$K_P$によって、制御入力全体のだいたいの大きさが決められます。限界感度法では、Pゲインを、安定限界時のゲイン$K_u$の半分くらいの値に設定していますね。
安定限界時の入力は、超ざっくり言うと「出せる範囲内でのフルパワー」です。よってこれを基準に、そこからある程度余裕をもたせた値をPゲインに設定していると解釈できます。
またIゲイン・Dゲインは、それぞれ積分操作・微分操作によって、P制御の動作を補正する役割をするのでした。限界感度法では、Iゲイン・Dゲインを、安定限界時の周期$T_u$を元に求めています。
安定限界時の周期は、システムがフルパワーで動いたときの速さの指標となります。よってこれを基準に、IゲインとDゲイン(積分時間と微分時間)を決定していると解釈できます。
限界感度法の利点
限界感度法の最大の利点は、そのお手軽さです。難しい理論なしに、簡単な手順の実験を行うだけでPIDゲインを決定できます。
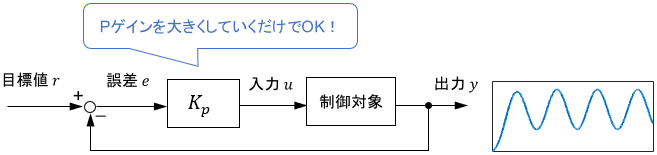

P制御を実験するだけでPIDゲイン全てが求まるので、非常にラクですよね!
限界感度法の欠点
とはいえ、限界感度法にはラクであるが故の欠点もあります。順番に説明していきましょう。
性能がよくない
まず、限界感度法で求めたPIDゲインで制御しても、実現される制御性能はあまり良くないことが挙げられます。
そもそも限界感度法は、絶対にうまくいくと理論的に裏付けされた手法ではなく、むしろ経験的なノウハウに近い手法です。
よって、限界感度法で得られるゲインが最適であることはまずなく、実用場面では手作業でさらにゲインを追い込む必要があります。
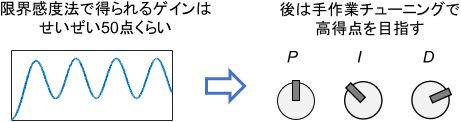

冷静に考えると、こんなシンプルな方法だけで、世の中の様々なシステムに全て対応できるわけありませんよね。

また、限界感度法を使った後、ゲインをより良いものに追い込むためには、結局PID制御や制御対象の知識が必要となります。
結局知識を使うのであれば、限界感度法を使わずに、最初から知識に基づいて手作業でゲインを調整したほうが、よりよい結果が得られることがほとんどです。
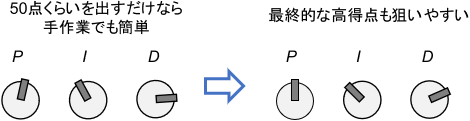

※手作業でのPIDゲインチューニングの方法については、こちらのページをご覧ください
安定限界まで動かすので、安全性に注意が必要
限界感度法では、システムが安定限界になるまでPゲインを上げる必要がありました。
システムの限界ギリギリで動かすと、どうしても安全性や故障のリスクが高くなってしまうので、注意が必要です。
ちょっとくらいムチャできるシステムなら問題ありませんが、安全性が重視されたり、故障が許されないシステムに対して使う場合は、本当に実行して大丈夫かよく確認しましょう。


ベースとなる知見が古い
限界感度法は、1942年に提案されためちゃくちゃ古い手法です。
1942年というと、ボード線図が考案されて間もないくらいの時期であり、制御工学はまだ学問として確立しきっていませんでした。
※そのあたりを含めた古典制御の歴史については、こちらのページをご覧ください(面白いよ!)
そんな時代の手法を、制御工学が発達した現在になっても使うとなると、結構時代遅れ感がありますよね。
もちろん有用であればいくら古くても使ったらよいのですが、これまで述べてきた欠点があることはしっかりと認識しておくべきでしょう。
実際のところ、制御工学に詳しい人ほど限界感度法に対する印象はよくないのが現実です。


限界感度法の使い所
そんな限界感度法ですが、使い所によっては非常に便利です。何事も適材適所というわけですね。
以下、限界感度法が有効に使える場面について紹介していきます。
そんなに性能がいらないとき
上で「性能がよくないことが欠点」といいましたが、そもそもそんなに性能がいらないときには何の問題もありません。

ただ前述の通り、そこそこの性能であれば手作業チューニングでも簡単に実現できるので、本当に限界感度法が必要かどうかを検討する余地はあります。
知識ゼロだけど今すぐなんとかしたいとき


制御なんて全然知らないけど、今すぐチューニングする必要が出た!どうしよう!
という緊急の場合には、藁にもすがる思いで限界感度法を活用するのはアリでしょう。ただ前述の通り、限界感度法は安全性に注意が必要なので、そこだけはよく確認しておく必要があります。
また、何らかの理由で、制御の知識がない人にチューニングを頼む必要が出た際にも、使える可能性はありますね。

ただし、1,2時間ほどPID制御を勉強すれば、手作業チューニングで限界感度法よりもよい結果を出せるようになると思いますので、本当に緊急のときの最終手段にすることをおすすめします。
自分のチューニングにどうしても自信が持てないとき
手作業でいくらチューニングしてもどうしても思うような性能がでないときに、チューニングの参考に限界感度法の結果を見てみることは有効です。
もし限界感度法の結果のほうがよければ、それをベースに手作業チューニングで性能を追い込めばOKです。逆に限界感度法の結果のほうが悪ければ、そのシステムで出せる限界はその程度だと分かります。(たいていは後者になると思います)

※ちなみに、限界感度法によく似た「ステップ応答法」と呼ばれる手法もそこそこ有名です。これに関しても、利点・欠点・使い所は、上記とほぼ同じと考えてOKです。
以上、 限界感度法の概要と、その利点・欠点・使い所についての解説でした。
- 限界感度法は、簡単でお手軽であるのが最大の利点
- 性能が悪く、安全性に注意が必要なのが欠点
- 基本的には限界感度法を使わず、手作業でチューニングしたほうがよい結果が得られる
- 緊急時の最後の手段や、参考情報としては使える






コメント