PID制御のプログラム例。仕組みと考え方を詳しく解説！

このページでは、PID制御器のプログラム例と、その考え方を詳しく解説します。

※PID制御の基礎を未学習の方は、まずこちらのページをご覧ください

PID制御とは？仕組みと動作イメージを分かりやすく解説！

このページでは、PID制御について、2次系を対象にその仕組みと動作イメージを解説します。 このページのまとめ PID制御は、使いやすさが最大の特徴。 面倒な計算をしなくても、80点くらいの性能を手軽に出せる。 Pの項はバネ。出力を目標値に近...

controlabo.com

2023.06.06

動作条件

まず、前提となるシステム構成を確認しておきましょう。次のようなブロック線図で表される、PID制御システムを考えます。

このシステムにおける制御入力$u$は、PID制御器によって次式で計算されるのでしたね。

$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{比例\ P} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{積分\ I} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{微分\ D}$$

$K_P,K_I,K_D$は、それぞれP・I・Dゲインです。上式を使うと、いかなる時刻$t$に対しても、そのときの入力$u(t)$が導出可能となります。

ただ、逆に言うと、これを厳密に実現させるには、無限に短い周期で入力を更新し続ける必要があることになります。

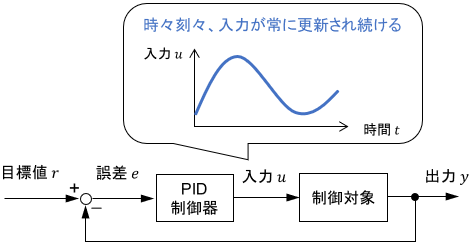
今、PID制御をプログラムで実現させようとしているので、そんなことは実現不可能ですよね。いくら高性能なCPUでも、無限に短い周期でプログラムを走らせることはできません。

よって、プログラムによって現実のシステムを制御する際は、次のように一定の制御周期ごとに入力を更新する構成をとることがほとんどです。

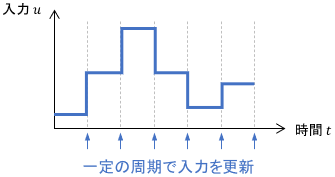
次の制御周期が来るまでの間は、制御器は何もできないので、上図のように入力を一定に保持しておくのが一般的です。

とりあえずは、制御周期を小さくすればするほど、本来の式に近い制御が達成できるとイメージしておけばOKです。

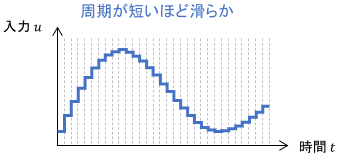
ただし、制御周期内でプログラム上のすべての演算を終わらせる必要があるため、システムに求められる要件は厳しくなります（例えば高いCPUスペックか、少ない演算量が必要となる）。

とはいえPID制御の場合は、制御周期を小さく設定しても問題になることはほとんどありません。すぐ後で示すようにプログラムが数行で済むので、短い周期でも演算が間に合うことがほとんどだからです。

制御周期の適正値は、対象システムの特性や要求性能しだいですが、例えば機械システムなら1～10msくらいを想定しておけばよいでしょう。

PID制御器のプログラム例

それでは、プログラムを具体的に見ていきましょう。

まずはコアとなるPID制御器のプログラムです。これは次式を計算するだけなので、結構簡単に実装できます。

$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{比例\ P} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{積分\ I} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{微分\ D}$$

// 下記変数は既に与えられているものとする
// y       : 現在の出力
// r       : 現在の目標値
// e_pre   : 前回の誤差
// T       : 制御周期
// KP,KI,KD: P,I,Dゲイン

// PID制御の式より、制御入力uを計算
e  = r - y;                // 誤差を計算
de = (e - e_pre)/T;        // 誤差の微分を近似計算
ie = ie + (e + e_pre)*T/2; // 誤差の積分を近似計算
u  = KP*e + KI*ie + KD*de; // PID制御の式にそれぞれを代入

かなりシンプルですね。これを制御周期ごとに呼び出せば、各時刻における制御入力が求まるというわけです。

なお、Dの項に含まれる誤差の微分$\dot{e}(t)$（変数でいうと de）は、次のように数値微分で近似的に求めています。

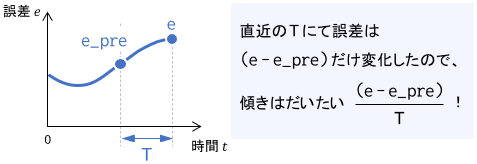
また、Iの項に含まれる誤差の積分$\int ^t _0 e(\tau) d\tau$（変数でいうと ie）は、次のように数値積分で近似的に求めています。

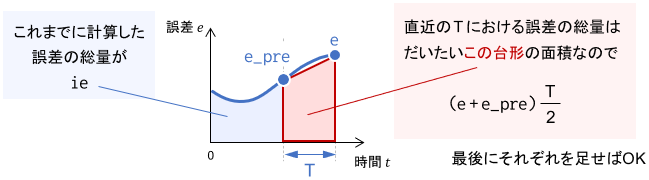
これらの近似には必ず誤差が含まれてしまいますが、制御周期を十分小さくとっていれば、実用上問題になることはほとんどありません。

全体プログラム（お手軽版）

上記プログラムに、各種変数を取得（または定義）するプログラムも追加して、全体像を把握しましょう。

// 定数設定 ===============
KP = 20;  // Pゲイン
KD = 5;   // Dゲイン
KI = 1;   // Iゲイン
T  = 0.01;// 制御周期[秒]

// 変数初期化 ===============
e_pre = 0; // 微分の近似計算のための初期値
ie = 0;    // 積分の近似計算のための初期値

// メインループ ===============
while(1){
  // 制御周期分だけ待つ処理
  sleep(T);

  // 現時刻における情報を取得
  y = get_y(); // 出力を取得。例:センサー情報を読み取る処理
  r = get_r(); // 目標値を取得。目標値が一定ならその値を代入する

  // PID制御の式より、制御入力uを計算
  e  = r - y;                // 誤差を計算
  de = (e - e_pre)/T;        // 誤差の微分を近似計算
  ie = ie + (e + e_pre)*T/2; // 誤差の積分を近似計算
  u  = KP*e + KI*ie + KD*de; // PID制御の式にそれぞれを代入

  // 制御入力をシステムに与える処理
  give_u(u); // 例:モーターに電流を流す処理

  // 次のために現時刻の情報を記録
  e_pre = e;
}

プログラム内の処理の詳細は、コメントに書いてある通りです。

sleep()、get_y()、get_r()、give_u()といった関数は、対象システムや使用言語に応じて書き換えてくださいね。

全体プログラム（細かい所までちゃんとしてる版）

上記プログラムは分かりやすさを重視したものなので、制御性能の向上や、理論的な正確性という観点ではちょっぴり改善の余地があります。（そのままでも結構ちゃんと動いてくれますが）

ここからは、それらを反映したマイナーチェンジ版や、設計時の考え方について詳しく紹介していきましょう。

時間待ち処理

先ほどのプログラムでは、単純に制御周期分だけ待機することで、周期的な制御を実現していました。

// メインループ ===============
while(1){
  // 制御周期分だけ待つ処理  
  sleep(T);
 コレ
︙

ただし、これでは実質的な周期が「プログラムの処理時間＋待機した時間」となり、設定した制御周期が厳密には実現できないことに注意が必要です。

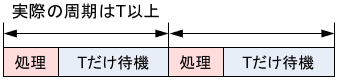
前述の通りPID制御の計算は時間がかからないため、「ほぼ一瞬」とみなせば、正直そこまで大きな問題にはなりません。

ただし、例えばセンサー情報の取得など、PID制御以外の処理に時間がかかる場合は、制御周期が意図したものからズレてしまいます。

このような問題を防ぐためには、実際に時間を計測し、次のように処理時間も含めて制御周期を考慮するプログラムを書けばOKです。

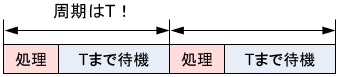
上記を反映したプログラムがこちらです。（変更部分をオレンジで囲んでいます）

// 定数設定 ===============
KP = 20;  // Pゲイン
KD = 5;   // Dゲイン
KI = 1;   // Iゲイン
T  = 0.01;// 制御周期[秒]

// 変数初期化 ===============
e_pre = 0; // 微分の近似計算のための初期値
ie = 0;    // 積分の近似計算のための初期値

// メインループ ===============
timer_start(); // 時間の計測を始める関数。timer_now()で計測値取得
while(1){
  // 制御周期分だけ待つ処理
  while(timer_now() < T); // 制御周期分の時間が経つまで待つ
  timer_start();          // 時間の計測を再び0から開始

  // 現時刻における情報を取得
  y = get_y(); // 出力を取得。例:センサー情報を読み取る処理
  r = get_r(); // 目標値を取得。目標値が一定ならその値を代入する

  // PID制御の式より、制御入力uを計算
  e  = r - y;                // 誤差を計算
  de = (e - e_pre)/T;        // 誤差の微分を近似計算
  ie = ie + (e + e_pre)*T/2; // 誤差の積分を近似計算
  u  = KP*e + KI*ie + KD*de; // PID制御の式にそれぞれを代入

  // 制御入力をシステムに与える処理
  give_u(u); // 例:モーターに電流を流す処理

  // 次のために現時刻の情報を記録
  e_pre = e;
}

時間を計測するための関数 timer_start() や timer_now() は、対象システムや使用言語に応じて書き換えてください。

微分計算

続いては、微分計算についてです。

前述のように数値微分そのものに大きな問題はないのですが、上記プログラムでは「前回計算した誤差」を表す変数 e_pre の初期化に少し問題があります。

プログラムの最初の段階では、e_preは「制御開始時点での誤差」を表すわけですが、それを簡易的に0としていましたね。

// 変数初期化 ===============
e_pre = 0; // 微分の近似計算のための初期値
ie = 0;    // 積分の近似計算のための初期値

ただ、制御開始時点での誤差は常に0であるとは限りません。よって、実際の誤差を計算し、それを用いて初期化するように変更しましょう。（下記のオレンジの部分です）

// 定数設定 ===============
KP = 20;  // Pゲイン
KD = 5;   // Dゲイン
KI = 1;   // Iゲイン
T = 0.01; // 制御周期[秒]

// 変数初期化 ===============
ie = 0;   // 積分の近似計算のための初期値設定
// 微分の近似計算のための初期値をより適切に設定
y = get_y();   // 出力を取得
r = get_r();   // 目標値を取得
e_pre = r - y; // 誤差を計算

// メインループ ===============
timer_start(); // 時間の計測を始める関数。timer_now()で計測値取得
while(1){
  // 制御周期分だけ待つ処理
  while(timer_now() < T); // 制御周期分の時間が経つまで待つ
  timer_start();          // 時間の計測を再び0から開始

  // 現時刻における情報を取得
  y = get_y(); // 出力を取得。例:センサー情報を読み取る処理
  r = get_r(); // 目標値を取得。目標値が一定ならその値を代入する

  // PID制御の式より、制御入力uを計算
  e  = r - y;                // 誤差を計算
  de = (e - e_pre)/T;        // 誤差の微分を近似計算
  ie = ie + (e + e_pre)*T/2; // 誤差の積分を近似計算
  u  = KP*e + KI*ie + KD*de; // PID制御の式にそれぞれを代入

  // 制御入力をシステムに与える処理
  give_u(u); // 例:モーターに電流を流す処理

  // 次のために現時刻の情報を記録
  e_pre = e;
}

上記では、分かりやすさのためにオレンジと緑の部分でほぼ同じ処理を2回書いていますが、この部分を関数としてまとめれば、よりデバッグ効率を上げられるでしょう。

// 以下の処理を関数にまとめ、eとe_preの計算に使うとなおよい
y = get_y(); // 出力を取得
r = get_r(); // 目標値を取得
e  = r - y;  // 誤差を計算して返す

積分計算

「誤差の積分値」を表す変数 ie の初期値は、とりあえず0にしておけば暴走することはありません。ただ、場合によっては0以外に設定したほうが制御性能を上げられることは覚えておきましょう。

// 変数初期化 ===============
ie = 0;    // 積分の近似計算のための初期値設定

例えば制御開始直後にシステムに大きな外乱が加わる場合は、ie をその外乱と釣り合うくらいの値で初期化しておけば、制御初期の外乱の影響を低減できます。

※詳しくはこちらのページの最後の方の「Iの項の初期値を設定する」という項目で解説していますので、合わせてご覧ください。

実践PIDゲインチューニング。失敗しない調整の極意とは？

PID制御の基礎理論は勉強した。PIDゲインのイメージも何となく分かった。でもPIDゲインチューニングって具体的にどう進めたらいいんだ！？ という疑問を解決するために、このページでは、2次系を想定したPIDゲインチューニングの実践的な方法の...

controlabo.com

2024.03.25

変数の記録

上記を反映させればPID制御がしっかり動いてくれるはずですが、後で制御結果を評価・分析するために、必要に応じて各種変数を配列などに記録＆保存する処理を追加しておくと良いでしょう。（このあたりの書き方は言語によるので、具体例は省略します）

最低でも各時刻での入出力信号は記録しておき、後は必要に応じて誤差やPID各項の値などを控えておくとよいでしょう。

※制御結果の分析方法（どのデータをどう見るか）については、こちらのページにまとめていますので、参考にしてください。

制御結果の分析法基礎。失敗しないための着眼点とは

構築した制御システムがうまく動かなかったときは、その原因を分析する、デバッグ作業を行う必要があります。 制御結果の分析・デバッグ方法は制御の種類や目的によって様々ですが、このページでは、どんなケースにも共通する基礎的な考え方について解説しま...

controlabo.com

2023.06.06

ここまでの変更点を全て反映させると、プログラムは次のようになります。

// 定数設定 ===============
KP = 20;  // Pゲイン
KD = 5;   // Dゲイン
KI = 1;   // Iゲイン
T = 0.01; // 制御周期[秒]

// 変数初期化 ===============
ie = 0;   // 積分の近似計算のための初期値設定(対象に応じて調整)
// 微分の近似計算のための初期値設定
y = get_y();   // 出力を取得
r = get_r();   // 目標値を取得
e_pre = r - y; // 誤差を計算

// メインループ ===============
timer_start(); // 時間の計測を始める関数。timer_now()で計測値取得
while(1){
  // 制御周期分だけ待つ処理
  while(timer_now() < T); // 制御周期分の時間が経つまで待つ
  timer_start();          // 時間の計測を再び0から開始

  // 現時刻における情報を取得
  y = get_y(); // 出力を取得。例:センサー情報を読み取る処理
  r = get_r(); // 目標値を取得。目標値が一定ならその値を代入する

  // PID制御の式より、制御入力uを計算
  e  = r - y;                // 誤差を計算
  de = (e - e_pre)/T;        // 誤差の微分を近似計算
  ie = ie + (e + e_pre)*T/2; // 誤差の積分を近似計算
  u  = KP*e + KI*ie + KD*de; // PID制御の式にそれぞれを代入

  // 制御入力をシステムに与える処理
  give_u(u); // 例:モーターに電流を流す処理

  // 次のために現時刻の情報を記録
  e_pre = e;

  // 以下、各変数の現在の値を記録する処理を追加するとなおよい
}

以上、PID制御のプログラム例についての解説でした！