
PID制御の基礎理論は勉強した。PIDゲインのイメージも何となく分かった。でもPIDゲインチューニングって具体的にどう進めたらいいんだ!?
という疑問を解決するために、このページでは、2次系を想定したPIDゲインチューニングの実践的な方法の一例を解説します。
PIDゲインの基本性質に基づいて、各種ゲインを試行錯誤的にちょっとずつ調整するチューニングもアリ(というかそのような工程は絶対必要)ですが、このページで解説するのはそれよりさらに1歩ステップアップしたチューニング方法です。
※PIDゲインの基本性質について未学習の方は、まずこちらのページをご覧ください。
このページを読めば、試行錯誤チューニングや、限界感度法を用いたチューニングよりは良い性能が得られるようになるでしょう。
※限界感度法はそこそこ知名度のあるPIDゲイン調整手法ですが、当サイトでは使用をオススメしていません。詳細は、こちらのページをご覧ください。
PIDゲインチューニングの手順
- 制御器の構造を決める
- 制御ゲインの適切な大きさを求める(これが隠れた極意)
- ステップ目標値に対してゲインチューニングする。PDIの順で繰り返し追い込んでいく
- 目標軌道があれば、それに対してゲインを微調整する
例題設定:ロボットアームの角度制御
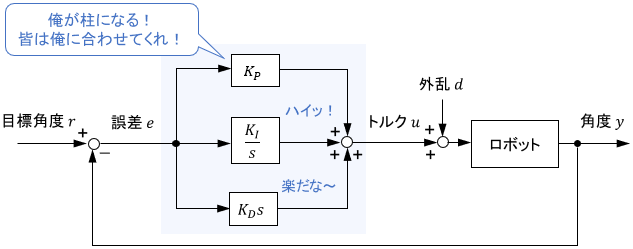
それでは、具体例を通じてPIDゲインチューニングの方法を学んでいきましょう。例題として、次のロボットアームの角度制御を考えます。
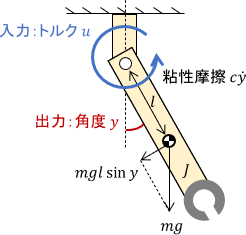
入力はアームに加わるトルク$u(t)$、出力はアームの角度$y(t)$、$J$は回転軸まわりのアームの慣性モーメント、$m$はアームの質量、$c$は粘性摩擦係数、$l$は回転軸から重心までの距離、$g$は重力加速度です。以降、それぞれの値は次の通りとします(トルク$u$の範囲以外はそんなに気にしなくてOKです)。
| 物理量 | 値 | 単位 |
|---|---|---|
| アームが出せるトルク$u$の範囲 | $-70 \leq u \leq 70$ | $\mathrm{N m}$ |
| 回転軸まわりのアームの慣性モーメント $J$ | $3$ | $\mathrm{kg m^2}$ |
| アームの質量 $m$ | $10$ | $\mathrm{kg}$ |
| 粘性摩擦係数 $c$ | $1$ | $\mathrm{N m s/rad}$ |
| 回転軸から重心までの距離 $l$ | $0.5$ | $\mathrm{m}$ |
この条件にて、ロボットアームを±20°の範囲、かつ6秒周期のsin波状に動かしたいとします。つまり、制御の目標値$r$は次式で表されます。
$$r(t)=20\sin\big(2\pi \cdot \frac{1}{6} \cdot t\big)\ [°]$$
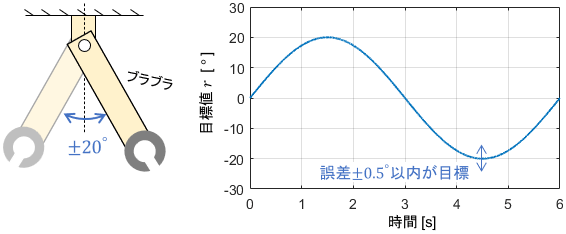
現状の制御器では、この目標値に誤差±3°の精度で追従できているとします。今回のPIDゲインチューニングでは、この追従誤差を±0.5°以内に低減させることを目的としましょう。
以降、この例題を通じてPIDゲインチューニングを実施していきます。PIDゲインチューニングの大まかな流れは次の通りです。それぞれ順番に説明していきましょう。
- 制御器の構造を決める
- 制御ゲインの適切な大きさを求める
- ステップ目標値に対してゲインチューニングする
- 目標軌道があれば、それに対してゲインを微調整する
手順1:制御器の構造を決める
概要
まず制御器の構造、すなわちP・I・Dのどの項を使うのかを決定しましょう。
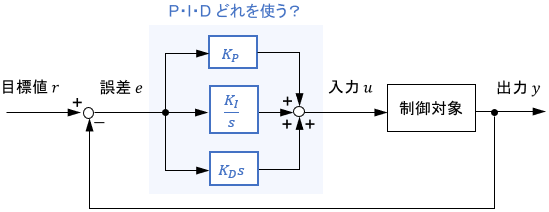
土台となる制御器を不適切に設定してしまうと、ゲインチューニングしてもよい性能が得られにくくなってしまうので注意が必要です。
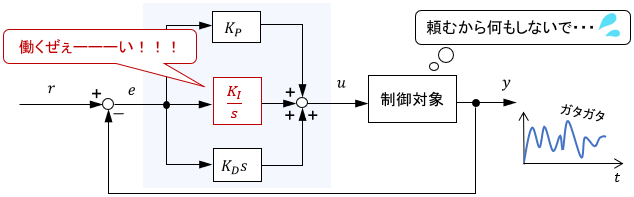
で、どう選べばよいかですが、ざっくりした指針としては次のイメージを持っておけばよいでしょう。
- Pの項:基本要素として必須。これをベースに、必要に応じて他の項を追加する
- Iの項:出力が目標値に留まるのを邪魔する、何らかの作用がシステムに働く場合に追加する
- Dの項:システムに振動を抑制する要素が十分にない場合に追加する
このイメージを念頭に、制御の目的・制御の条件・制御対象の性質を整理&検討しながら、臨機応変に制御器を決定します。詳しくはこちらのページで解説していますので、合わせてご覧ください。
具体例で確認
それでは、ロボットアームの例題にて、制御器の構造を決定していきましょう。
先ほどの指針に基づくと、Pの項は必須として、考えるべきはI・Dの項の必要性ですね。
Iの項についてですが、今回はアームに重力が作用し、角度を一定に保つ邪魔をします。よって、その影響を打ち消すためにIの項が必要となります。
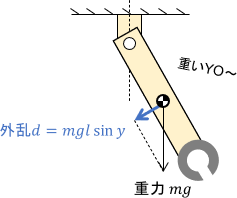
Dの項についですが、アームには小さな摩擦が働くだけで、振動抑制機構が備わっているわけではありません。よって、振動を打ち消すためにDの項も必要と言えるでしょう。

以上より、今回の場合は、P・I・D全ての項を使ったPID制御器を使うとよいことになります。
手順2:制御ゲインの適切な大きさを求める
概要
制御器が決まったので、次はいよいよ制御ゲインの検討に着手しましょう。まずは、下記手順で制御ゲインの適切な大きさを求めていきます。
- 入力の適切な大きさを決める
- 入力の内訳(P・I・Dの各項が受け持つ割合)を決める
- 上記情報から、制御ゲインの適切な大きさを逆算する
こうして制御ゲインの適切な大きさを知っておくと、システムの能力を過不足無く引き出すことが可能となります。地味な工程ですが、これがゲインチューニングの隠れた極意であるとも言えるでしょう。
逆に適切な大きさを把握せずにチューニングすると、見当外れな大きさの入力をシステムに与えてしまう恐れがあり、大変危険ですので注意が必要です。

具体的な方法は、例題に基づいて説明したほうが分かりやすいため、さっそく例題に移りましょう。
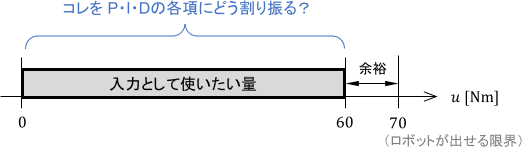
入力の適切な大きさを決める
まず、入力の大きさを決めていきます。これは、システムのスペック上の限界からある程度余裕を持たせた大きさを考えればOKです。詳しく説明していきましょう。
PID制御の理論上は入力に制限がありませんが、当然どんなシステムにも「装置の能力的に出せるのはこの範囲」、「これ以上出すと装置が壊れる」といった現実的に許される範囲がありますよね。

よって、制御前に入力の適正範囲をしっかり把握し、制御中はその範囲を必ず守る必要があります。
今回のロボットアームの例題では、アームが出せる入力(アームに与えてよい入力)が$-70 \leq u \leq 70\mathrm{[Nm]}$と与えられていましたね。今回は、この範囲がそのまま入力の適正範囲ということになります。
一般的には、たくさん入力を与えてグイグイ制御したほうが、制御性能は向上します。よって設計上の方針としては、上記の範囲内でなるべく大きな入力を使うことを目指すことになります。
とはいえ上限ギリギリを狙いすぎると、誤差・ノイズ・外乱等の影響で動作条件が想定からズレた際に、入力が適正範囲を超えてしまう恐れがあります。よって、現実には入力の大きさとして、適正範囲の上下限からある程度余裕を持った値を目指す必要があります。

どれほどの余裕を持つべきかは、「動作条件がどれくらい想定からズレうるか」や「もし入力が適正範囲を超えるとどれほどヤバいか」などを基準に、システムに合わせてケースバイケースで決定する必要があります。
例えば乱暴に扱っても大丈夫なシステムであれば、上限の90%以上の入力を狙ってもよいかもしれません。逆にとにかく安全性を重視するシステムでは、50%以下の入力が適正になる場合もあるでしょう。
今回のロボットアームの場合を考えてみましょう。まず、ロボットアームには重力以外の外乱が加わらず、動作条件は想定から大きくズレにくいと言えます。また、入力が適正範囲を超えても(一時的に無理な負荷がかかりますが)ただちに装置が壊れるわけでないとしましょう。
これらより、入力の大きさ(符号を除いた絶対値)としては上限の約85%の60[Nm]を目指すこととしましょう。

入力の内訳(P・I・Dの各項が受け持つ割合)を決める
入力の大きさが決まったので、次は「入力をP・I・Dの各項が受け持つ割合」を決めましょう。D・I・Pの順に説明していきます。
Dの項
Dの項を振動抑制のためだけに使う場合、基本的にDの項はマイナスの作用(入力にブレーキをかける作用)を及ぼすことになります。
よって、Dの項が入力のリソースを大量に消費することはほぼなく、割合は0と考えて大丈夫でしょう。

Iの項
続いてIの項です。Iの項は、外乱に抗い、出力を目標値に保持する作用をするのでしたね。よって、Iの項には外乱に抗うのに十分な量の入力を割り当てておく必要があります。(Iの項を使わない場合は割り当て無しでOKです)
ロボットアームの例題で考えてみましょう。アームには、外乱として重力が作用するんでしたね。その大きさは、アームの角度によって変化します。
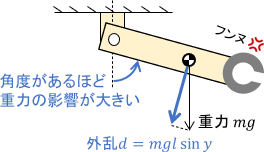
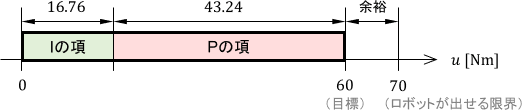
今回は±20°の範囲でアームを動かすため、外乱の最大値は次式で求まります。
$$外乱dの最大値=mgl\sin (y_{\max}) = 10 \cdot 9.8 \cdot 0.5 \cdot \sin 20^\circ \approx 16.76 \ \mathrm{[Nm]}$$
Iの項はこれにしっかり抗う必要があるため、これと同じだけの入力をIの項に割り当てておきましょう。

Pの項
最後はPの項です。設計の基本方針は「許される範囲内でたくさんの入力を使い、グイグイ制御する」でしたので、これに従い残りの入力リソースを全部Pの項に割り当てればOKです。
制御ゲインの適切な大きさを逆算する
P・I・Dそれぞれの項の大きさが決まったので、これらからゲインの適切な大きさを逆算していきましょう。
ゲインチューニングにおいては、P・I・Dの中でも制御の基本となるPゲインを適切に設定することが非常に重要です。
Iゲイン・Dゲインを計算によって求めることもできますが、労力に対してメリットはあまりありません。計算が複雑なのでPID制御の利点であるお手軽さが薄れてしまいますし、Pゲインを適切に設定していれば他のゲインは手作業チューニングでも結構簡単に適正値を求められるため、ここからはPゲインの適切な大きさを逆算することにフォーカスして説明していきます。
まず、PID制御のPの項を確認しましょう。
$$\begin{align}Pの項によって作られる入力\ u_P &= \osg{K_P}{ゲイン} \cdot \osg{e\vphantom{K_P}}{誤差}\quad なので、\\[7pt] Pゲインを逆算すると\ K_P &= \frac{u_P}{e}\end{align}$$
上式より、Pゲインを逆算するためには「Pゲインによって作るべき入力の大きさ$u_P$」と「Pの項に与えられる誤差の大きさ$e$」が必要であると分かります。
「Pゲインによって作るべき入力の大きさ$u_P$」は先ほど決めたので、これをそのまま使えばOKですね。

続いて、もう一つの情報である「Pの項に与えられる誤差の大きさ$e$」について考えていきましょう。
これは、平たく言うと「システムの動作時に想定される誤差の大きさ」です。過去の動作実績や、システムのスペックから「少なくともこれ以上にはならない」という値を考えればよいでしょう。
今回のロボットアームの例では、過去の動作実績より、少なくとも±3°の精度で動かせることが分かっていましたので、まずは誤差±3°を想定して進めていくことにしましょう。
目指す精度は±0.5°なので、この値を想定誤差とする考え方もありますが、チューニング前の段階ではそもそもこの精度が実現可能なのかどうかも不明です。もし実現不可能であれば想定が全て破綻してしまうので、最初は余裕を持った値を設定し、システムを実際に動作させながら徐々に絞っていくことをオススメします。(以降の例でもそうしていきます)

以上の通り、想定入力43.24Nm、想定誤差3°とすると、Pゲインの適切な大きさは次のように求まります。
$$K_P = \frac{u_P}{e} = \frac{43.24}{3} \approx 14.41$$
これはあくまで想定に基づいた参考値であるため、この値を絶対的な正解とするのではなく、これを基準に実際にシステムを動かしながらゲインを微調整していきましょう。
手順3:ステップ目標値に対してゲインチューニングする
概要
適切なゲインの大きさが見積もれたら、次はステップ目標値に対してゲインを詳細に調整していきます。
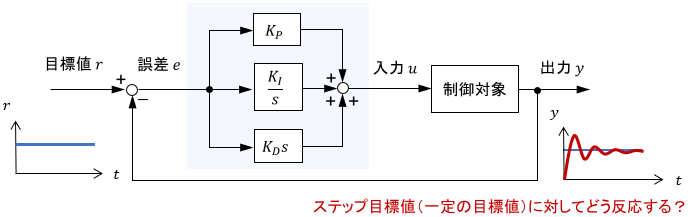
もし本番で用いるのがステップ目標値でなくても、ステップ目標値に対する出力(=閉ループシステムのステップ応答)は制御性能を評価する際の基本となるため、まずはステップ目標値を使うことをオススメします。
チューニングはだいたい次の流れで行うと間違いないでしょう。
- まず基本となるPゲインを設定する
- Dゲインを調整して、振動を抑制する
- Iゲインを調整して、定常偏差を抑制する
- 上記を繰り返し、ゲインを追い込んでいく
※閉ループシステムの詳細については、こちらのページをご覧ください
まず基本となるPゲインを設定する
それでは、ロボットアームの例題にて具体的に手順を確認していきましょう。
まず、目標値を設定します。ロボットの動作範囲は±20°だったので、目標値は外乱が強くも弱くもない10°とすることにしましょう。想定誤差を3°としていたので、アームの初期角度を7°として、それを10°に持っていく動作でチューニングを進めていきます。
次の通り、先ほど決めたPゲインのみを使って、P制御でシステムを動かしてみた結果がこちらです。
| ゲイン | 値 |
|---|---|
| P | 14.41(さっき決めた値) |
| I | 0 |
| D | 0 |
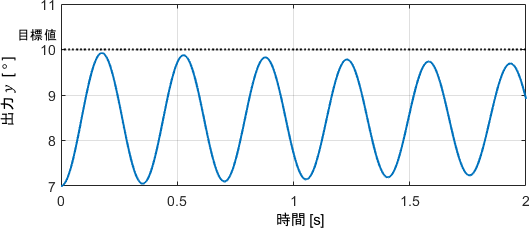
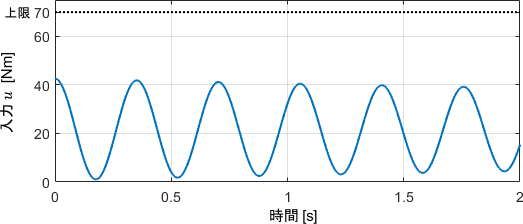
Pの項だけで制御しているので、出力が振動して目標値に収束していませんね。まあ想定通りでしょう。
ここで見るべきは、誤差3°に対して、入力が約43[Nm]と当初の狙い通りに出ていることです。時刻0のときの入出力をみると分かりやすいですね。

これにより、先ほど計算したPゲインの大きさが確かにこれで良さそうなことが、実際のシステムの挙動からも確認できたことになります。
ここからさらにD・Iゲインを追加して、制御性能を向上させていきましょう。
Dゲインを調整して、振動を抑制する
出力が振動していては動作の評価がしにくいので、まずはDゲインによって振動を抑制しましょう。
次の通り、先ほどの設定に対してDゲインを様々に変えた際の動作結果がこちらです。
| ゲイン | 値 |
|---|---|
| P | 14.41(さっきと同じ) |
| I | 0 |
| D | 色々変えてみる |
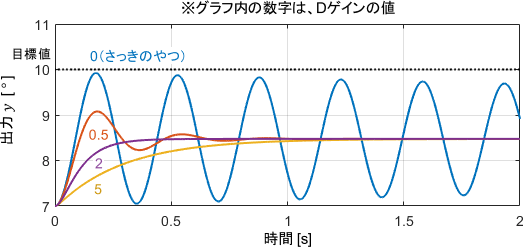
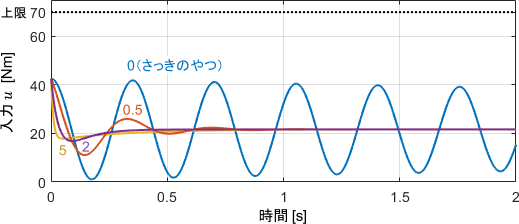
出力を見ると、Dの項の作用で振動が抑制されていることが分かります。
Dゲインの値としては2がよさそうですね。それより小さいと振動が残り、大きいとシステムの反応が遅くなってしまっています。
入力を見ると、変わらず想定通りの大きさが出ていることが分かりますね。つまり、Dの項を追加しても動作に支障が出ていないことが分かります。
Iゲインを調整して、定常偏差を抑制する
次に、Iゲインによって定常偏差を抑制していきましょう。
次の通り、先ほどの設定に対してIゲインを様々に変えた際の動作結果がこちらです。
| ゲイン | 値 |
|---|---|
| P | 14.41(さっきと同じ) |
| I | 色々変えてみる |
| D | 2(さっき決めた値) |
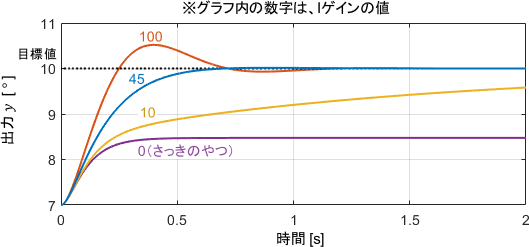
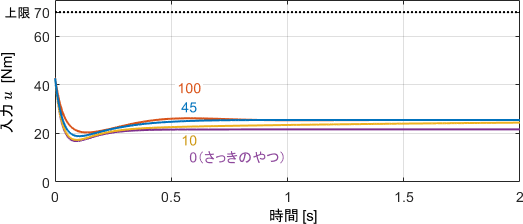
出力を見ると、Iの項が重力に抗うおかげで定常偏差が抑制されていることが分かります。
Iゲインの値としては45がよさそうですね。それより小さいと目標値への収束が遅くなり、大きいとオーバーシュートが生じてしまっています。
入力を見ると、Iの項を追加しても、意外と大きさが変わっていませんね。これは、Iの項が本格的に力を出し始める頃には誤差が小さくなっており、Pの項がほとんど力を出していないためです。システムとしてはまだ余力がありそうですが、とにかくIの項を追加しても動作に支障はなさそうですね。
システムに余力があるのであれば、もう少しシステムに頑張らせてもよさそうです。ただ、これはあくまでステップ目標値に対する結果なので、ゲインをこれ以上追い込む前に、まずは本番と同じ条件で動かして制御性能を確認すべきでしょう。
なお、今回の例ではすんなりと良さそうなゲインが求まりましたが、もし一発でうまくいかなければ、また上記の手順を繰り返し、ゲインを調整していけばOKです。
特に、Iゲインを追加すると振動が生じることがよくあります。この場合は、またDゲインを調整して振動を抑制し、それでもだめならPゲインを調整すればよいでしょう。
※本番でもステップ目標値を使う場合は、これにてチューニング完了です。
手順4:目標軌道があれば、それに対してゲインを微調整する
概要
最後に、本番で使う目標軌道を使って最終調整を行います。

既にステップ目標値でゲインを適切に調整できていれば、目標軌道にもかなりいい精度で追従するはずです。後は用途に応じてゲインを追い込んでいくわけですね。
なお、もし「これでいこう」と思えるよいゲインが見つかったら、最後にそのゲインでのステップ応答も合わせて確認し、基本性能を評価しておくことをオススメします。基本性能を知っておくことで、そのシステムをより安全かつ効率的に運用・保守できるためです。
よって、現実にはステップ目標値と目標軌道を何度か行ったり来たりしながらチューニングを進めることになるでしょう。
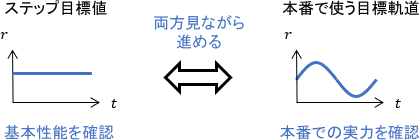
目標軌道に対して、制御性能を確認
早速、ロボットアームを目標軌道に追従させてみましょう。
ゲインを次の通りに設定した際の制御結果がこちらです。
| ゲイン | 値 |
|---|---|
| P | 14.41(さっきと同じ) |
| I | 45(さっき決めた値) |
| D | 2(さっきと同じ) |
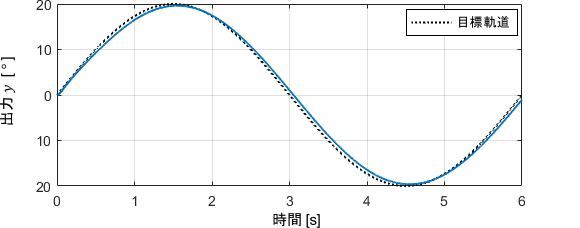
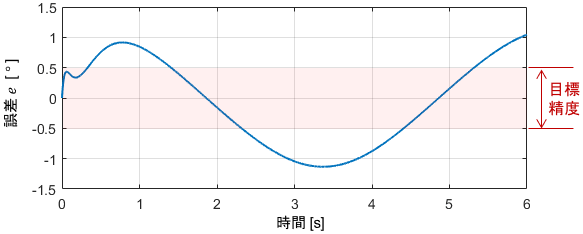

出力を見ると結構いい感じに追従できているようですが、誤差が1°ほど残っており、目標精度である0.5°を満たせていないことが分かります。
入力は最大で50[Nm]ほどであり、目標としている60[Nm]までまだ少し余裕があることも見て取れますね。よって、もう少しシステムに頑張らせるようにゲインを再調整して、精度を向上させていきましょう。
ゲインを再調整して、ステップ応答を確認
ゲインの再調整は、これまでやってきた工程を繰り返しながら、地道に進めることが基本となります。
今回の場合、現状のゲインで振動も定常偏差も十分に抑制できていることが、ステップ目標値に対する結果から分かっていました。よって、再調整をまず検討すべきは制御の基本となるPゲインでしょう。
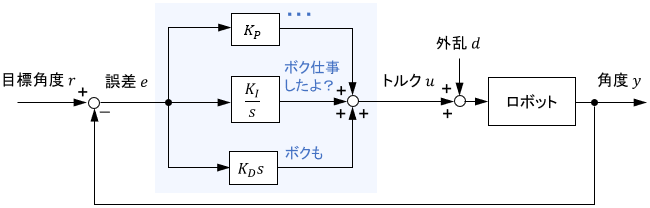
「目標軌道に対する挙動を見ながらPゲインを徐々に上げていく」という再調整もアリですが、今回の場合はPゲインの設定時に用いた誤差の想定量に改善の余地がありそうですので、この切り口で再調整をしてみることにします。
当初の誤差の想定量は、過去に動作の実績があった3°でした。ただ、先ほどの結果では誤差が1°にまで低減できていますね。よってこの結果を反映して、想定誤差1°にてPゲインを再設計してみましょう。
$$K_P = \frac{u_P}{e} = \usr{\frac{43.24}{\color{red}{1}} }{変更}\approx 43.24$$
このPゲインを基準として、先ほどと同様の手順でIゲイン・Dゲインをチューニングしましょう。想定誤差が1°なので、アームの初期角度を9°として、それを10°に持っていく動作でチューニングした結果がこちらです。

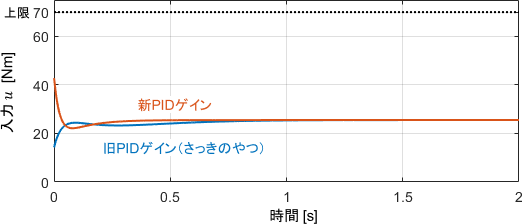
出力を見ると、旧ゲインではアンダーシュートが生じてしまっています。これは開始地点が9°に変わり、先ほどよりも重力がキツくかかるようになったためです。対して、新ゲインでは良好な性能が得られていますね。
入力も危なげない範囲で出ており、問題なさそうですね。ちなみに、このときのゲインは次の通りです。
| ゲイン | 値 |
|---|---|
| P | 43.24 |
| I | 200 |
| D | 3 |
目標軌道に対して、最終確認
それでは、先ほどのゲイン設定で、システムが本当に頑張ってくれるのかを確認してみましょう。
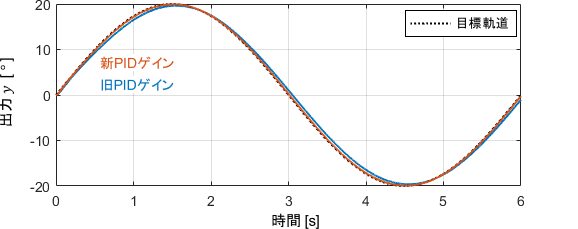
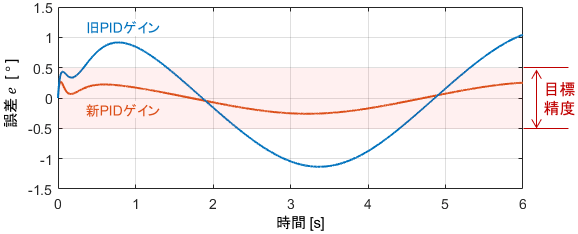
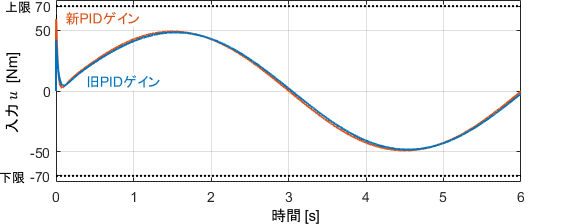
目標としている誤差±0.5°以内が達成されていますね!
入力を見ると、目標としていた60[Nm]が制御開始時点にてしっかりと出せていることも分かります。
これにてチューニング完了ですね!(もちろん必要に応じて、ここでさらに微調整を入れてもOKです)
その他のテクニック
ここからは、上の例では紹介しきれなかったその他の基本テクニックを簡単に紹介します。
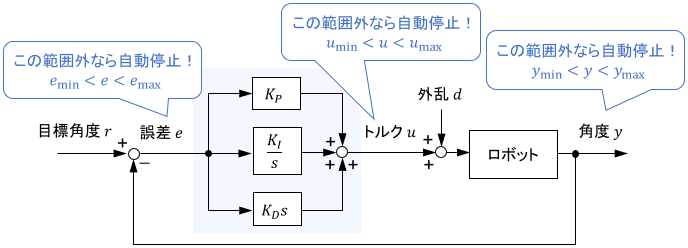
想定外の動作になったら自動停止させる
これまで紹介したゲインチューニング法では、入力の適正範囲・外乱の大きさ・誤差の大きさ等をある程度想定し、そこからゲインを逆算しました。
前述のとおり、もしこれらの想定が外れると、ゲインは適切な値から離れてしまいます。もし想定を大きく外すとシステムが暴走してしまう可能性もあるため、実用上はそれを防止する機能を設けておくべきでしょう。
具体的な方法は様々ありますが、代表例としては制御器(制御プログラム)にて入力・出力・誤差信号を常に監視し、その値が想定範囲外に入ったときにシステムを自動停止させることが挙げられます。
ステップ目標値が遠ければ、目標軌道を用意する
「途中経過はどうでもよいので、とにかく出力をある値に持っていきたい」という場合には、本番環境でもステップ目標値がよく使われます。
ただし、出力の目標値が初期値からかなり離れた所にある場合は、想定すべき誤差が大きくなり、制御性能に悪影響を及ぼすので注意が必要です。
例えば先ほどのロボットアームの制御にて、初期角度0°、目標角度180°とした場合を考えてみましょう。
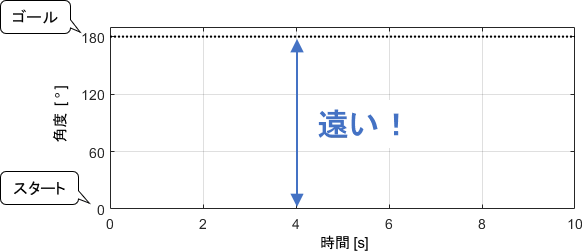
この場合、次のように制御開始直後と比較して目標値付近での入力が大幅に小さくなり、制御性能が低下してしまいます。
$$\begin{array}{lll} 誤差e=180^\circ &のとき、P項による入力は&u_P = 180K_P \\[5pt] 誤差e=1^\circ &のとき、P項による入力は&u_P = K_P \qquad \color{green}{1/180\ 倍!!}\end{array}$$
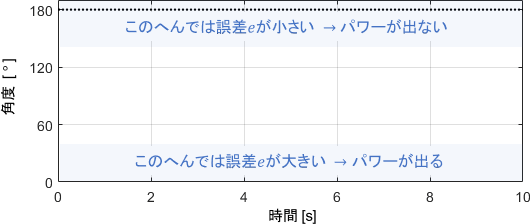
誤差1°の段階ではまだまだパワフルに頑張ってもらいたいので、これでは困りますね。これを防ぐには、出力を目標値まで導く目標軌道を用意するのが有効です。
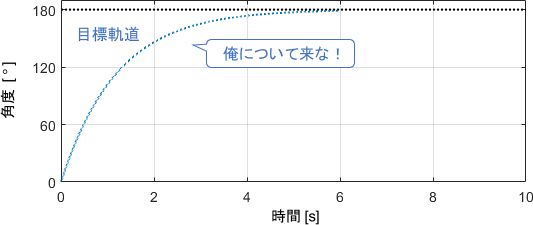
目標軌道を設計する手間は増えますが、これにより誤差の大きさが制御中を通じて大きく変化しなくなるため、制御性能の変動を防ぐことが可能となります。
ちなみに上図で用いた目標軌道は次式で表されるものであり、この手の用途によく使われます。
$$r(t) = K\Big( 1-e^{-\frac{1}{T}t}\Big)$$
$K$は最終的に持って行きたい値、$T$は収束の速さを調整する係数です。これはちょうど、ステップ状の目標値をゲイン$K$・時定数$T$の1次系に通した信号に等しくなります。
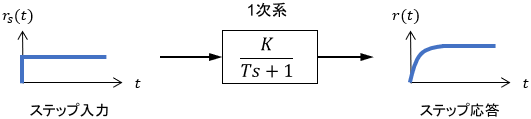
1次系の性質をうまく使った、まさに「制御工学的」な解決法であると言えるでしょう。
※1次系の性質の詳細については、こちらのページをご覧ください
Iの項の初期値を設定する
先ほどのロボットアームの制御にて、ゲインはそのままで腕の初期角度を20°に変更してみると、次のような挙動が得られます。
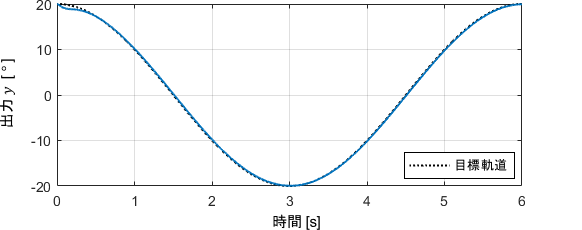
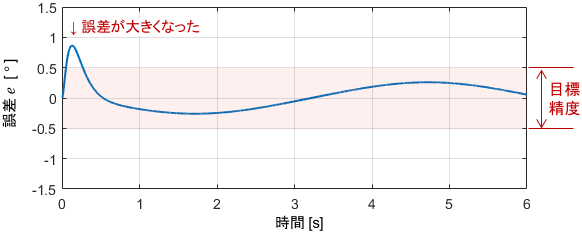
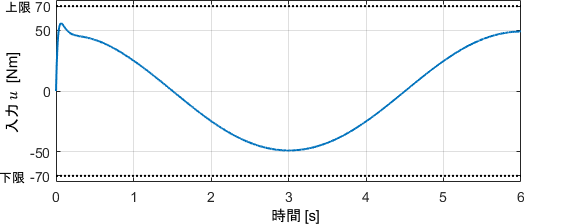
制御開始直後の誤差が大きくなっていますね。重力が一番キツくかかる姿勢で制御を開始したため、それに抗う力がIの項にて十分溜まるまでの間に、どうしても誤差が生じてしまうわけです。
これを防ぐには、外乱の大きさを事前に見積もり、その分をあらかじめIの項に入れておくことが有効です。
例えば先ほどの例では、腕の角度が20°のときにアームに加わる外乱を計算し、それをIの項に追加すればよいことになります。
$$外乱の初期量I_0=mgl\sin (y _{\max}) = 10 \cdot 9.8 \cdot 0.5 \cdot \sin 20^\circ \approx 16.76 \ \mathrm{[Nm]}$$
$$\mathrm{PID}入力u(t) = K_P\ e(t) + \biggl\{ K_I \int ^t _0 e(\tau) d\tau \color{green}{ +\usg{I_0}{追加!} }\biggr\} + K_D\ \dot{e}(t)$$
上式で制御した結果がこちらです。
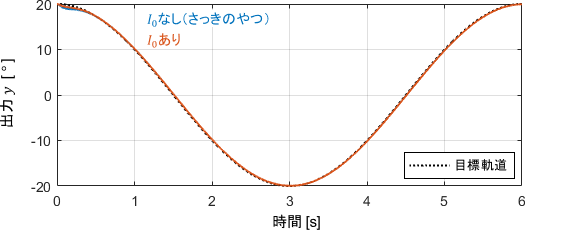
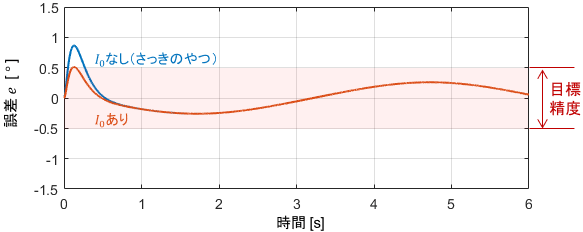
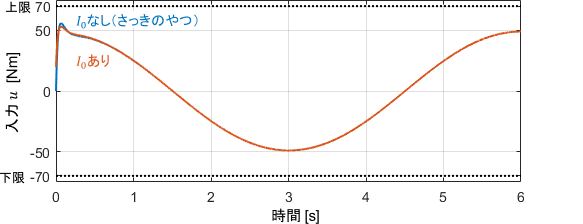
制御開始直後の誤差が低減されていることが分かりますね!
以上、PIDゲインチューニングの実践的な方法について、その一例を解説しました。
なお、上記方法は制御対象が2次系で表される場合に有効です。下記ページでは、制御対象が1次系や積分系で表される場合の取り扱いについて解説していますので、合わせてご覧ください。
PIDゲインチューニングの手順
- 制御器の構造を決める
- 制御ゲインの適切な大きさを求める(これが隠れた極意)
- ステップ目標値に対してゲインチューニングする。PDIの順で繰り返し追い込んでいく
- 目標軌道があれば、それに対してゲインを微調整する









コメント
このサイトでは何のアプリを使用してシミュレーションしてるんですか?
MATLABでシステムの微分方程式を解いてシミュレーションしています
この制御の場合、制御対象の関数はどのように設定しているのですか?
本ページの場合は、アームを剛体振子とみなし、その運動方程式を設定しています。
より具体的には、こちらのページで示している、近似前の運動方程式(Jθ” = -cθ’ – mglsinθ + τ)を使っています。