このページでは、PIDゲインの特性について、2次系を対象にゲインを様々に変化させたときの具体例を交えて解説します。
各種ゲインの特性をしっかり理解すれば、PID制御器の設計やチューニングをより効果的に行えるようになりますよ！
※このページは、こちらのページの続きです。このページだけ読んでも大丈夫ですが、PID制御の基本的な原理を未学習の方は、まずこちらをご覧ください。
- Pゲインが大きい：入力が大きくなり、動作は素早く、振動的になる
- Dゲインが大きい：ブレーキ力が大きくなり、動作は遅く、振動が抑制される
- Iゲインが大きい：外乱に抗う力を、勢いよく発生させる
問題設定
今回も簡単な機械システムを例題として、PIDゲインの特性を深掘りしていきましょう。
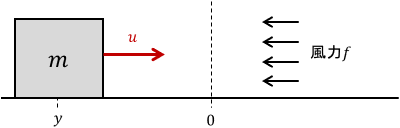
次のように、空気抵抗を受けながら動くブロックに力を与え、位置を0に持っていくことを考えます。
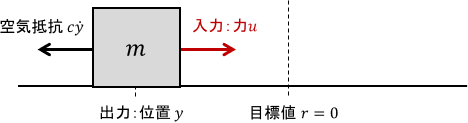
システムの入力はブロックに加わる力$u$、出力はブロックの位置$y$、目標値$r$は0ですね。
このシステムに対し、PIDゲインを大・中・小と3段階に変化させたときの挙動を比較していきましょう。（中がちょうどいい大きさで、大と小はそれよりも大きい／小さい、というイメージです）
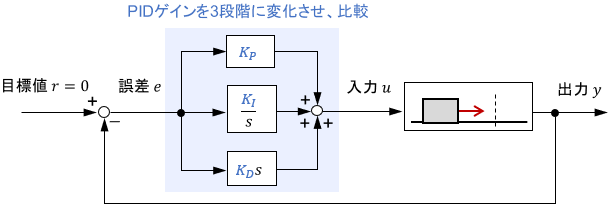
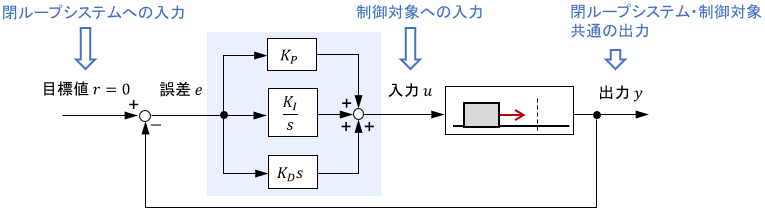
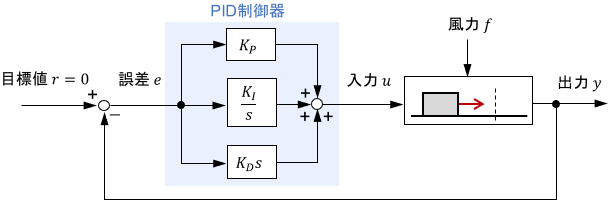
制御分析の極意は、「入力と出力の両方を確認し、両者の関係性を分析すること」でしたね。よってここからは、次の入出力信号に着目していきます。
- 閉ループシステムへの入力：目標値$r(=0)$
- 制御対象への入力：力$u$
- 閉ループシステム・制御対象共通の出力：位置$y$
※制御分析の基本や、閉ループシステムの意味については、こちらのページをご覧ください。
Pゲインの特性
まずはPゲインの特性を調べるために、システムにP制御（PID制御のPの項のみ）を適用します。
$$u(t) = \ubg{K_P\ e(t)}{Pの項} $$
Pの項は、出力を目標値に近づける、最も基本的な役割をするのでした。より具体的には、誤差が大きい（目標地点から遠い）ときには入力を大きく、誤差が少ない（目標地点に近い）ときには入力を小さくするように入力値を調整するんでしたね。その調整の度合いを決めるのがPゲインです。
今回は、そのPゲインを大・中・小と変化させてみましょう。それぞれのゲインに対して、システムは次のように動作します。
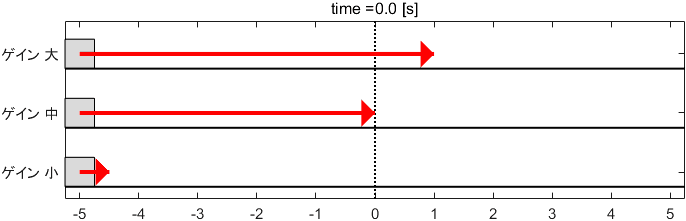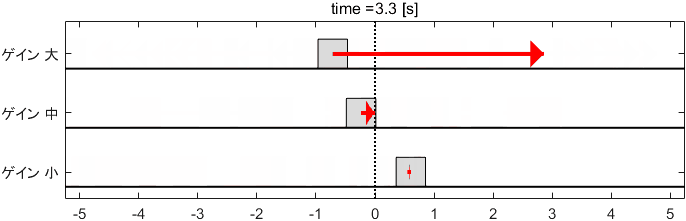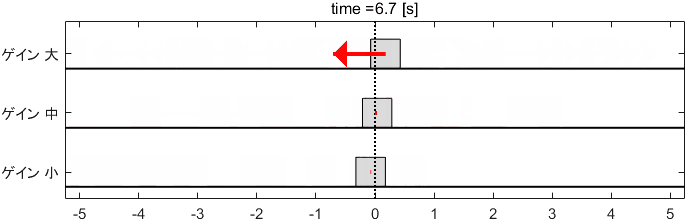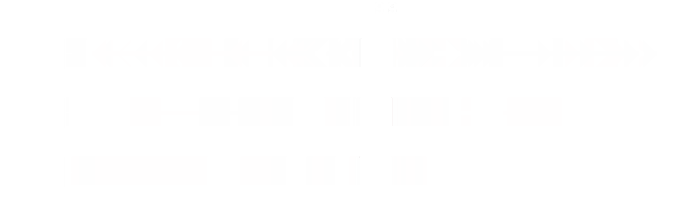
※矢印の長さが入力$u$の大きさを表しています（以降のアニメーションでも全部そうです）
…ゲイン大がめちゃくちゃ荒ぶってますね。ゲイン小は、もっと素早く動いて欲しい感じがします。ゲイン中はその中間ですね。
まとめると、だいたい次のような傾向が得られました。
- Pゲイン大：目標値に素早く向かう。振動的な挙動が大きい。
- Pゲイン中：目標値に中くらいの速度で向かう。振動も中くらい。
- Pゲイン小：目標値にゆっくり向かう。振動的な挙動は小さい。
動作データをグラフでも見てみましょう。位置$y$と入力$u$をプロットしたものがこちらです。
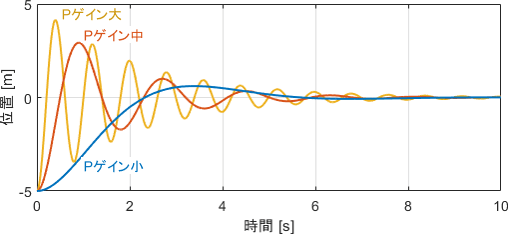
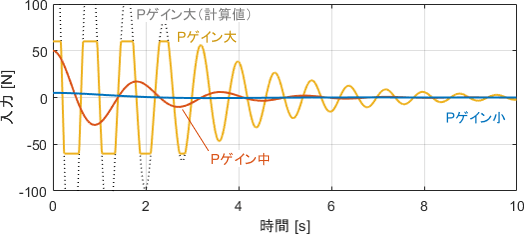
Pゲインに応じて入力の大小が決まり、入力が大きいほど動作が乱暴になることが読み取れますね。
また、今回は「機械のスペック上、±60[N]を超える入力は出せない」という設定にしています。よってPゲインを大きくした場合、計算上は±60[N]を超える入力が要求されているにも関わらず、システムはそれに応えられずに入力が頭打ちしてしまっています。
このような状態は「入力飽和が生じている」とよばれ、基本的には回避すべき悪いことだとされています。システムが制御器の意図通り動かない状態ですし、システム（ハードウェア）の能力の限界付近で動かすと故障のリスクが高まるからです。
Pゲインを上げすぎる（要求入力を上げすぎる）と、入力飽和のリスクもあることも覚えておきましょう。
Dゲインの特性
次にDゲインの特性を調べるために、システムにPD制御（PID制御のPとDの項）を適用します。
$$u(t) = \ubg{K_P\ e(t) }{Pの項} + \ubg{K_D\ \dot{e}(t)}{Dの項}$$
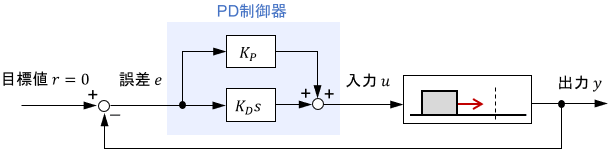
Dの項は、出力の振動を防ぐ役割をするのでした。より具体的には、実際の速度が目標速度を上回るときにはブレーキをかけ、下回るときには加速するように入力を調整するんでしたね。その調整の度合いを決めるのがDゲインです。
Pゲインを先ほどの「中」に設定し、Dゲインを大・中・小と変化させたときのシステムの挙動がこちらです。
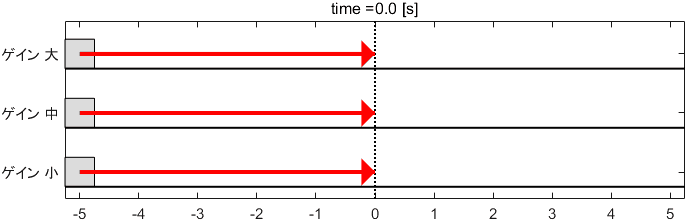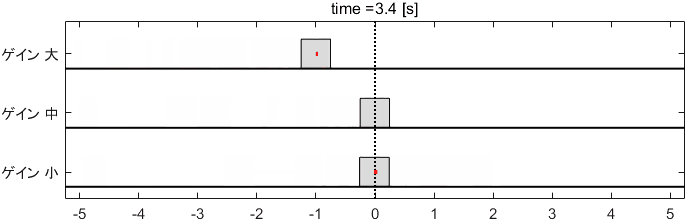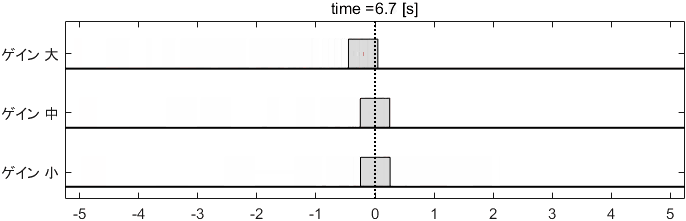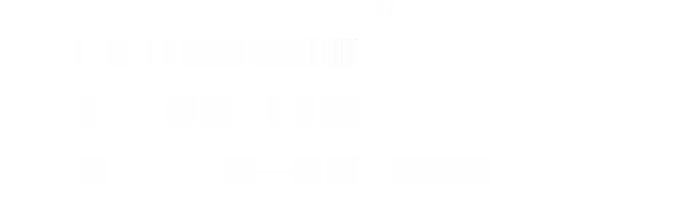
ゲイン大はブレーキが効きすぎており、ゲイン小はブレーキが効かなさすぎている、といった感じですね。
だいたい次のような傾向があるといえるでしょう。
- Dゲイン大：目標値にゆっくり向かう。振動なし。
- Dゲイン中：目標値にそこそこの速度で向かう。振動なし。
- Dゲイン小：目標値に素早く向かう。振動あり。
位置$y$と入力$u$をプロットしたものがこちらです。
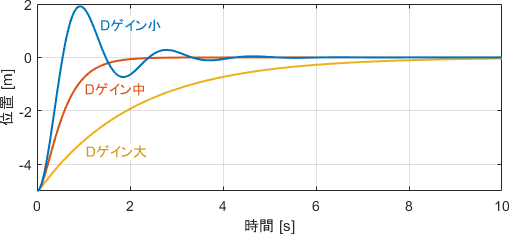
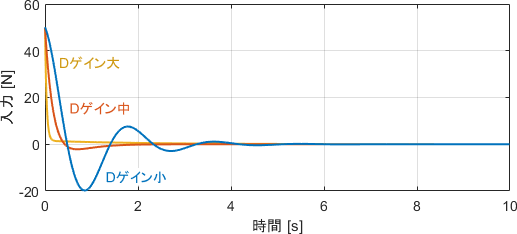
Dゲインが大きいほど入力が抑制され、動作がゆっくりになっていることが読み取れますね。
Iゲインの特性
最後はIゲインです。ここからは外乱として、一定の向かい風（風力$f$）をブロックに当てることにします。
この条件で、システムにPID制御を適用しましょう。
$$u(t) = \ubg{K_P\ e(t) \vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Pの項} + \ubg{K_I \int ^t _0 e(\tau) d\tau}{Iの項} + \ubg{K_D\ \dot{e}(t)\vphantom{K_I \int ^t _0 e(\tau) d\tau}}{Dの項}$$
Iの項は、外乱に抗い、出力を目標値に保持する役割をするのでした。より具体的には、制御開始時から今までの誤差の蓄積量（総和）に応じた力を入力に追加するんでしたね。その度合いを決めるのがIゲインです。
Pゲイン・Dゲインを先ほどの「中」に設定し、Iゲインを大・中・小と変化させたときのシステムの挙動がこちらです。
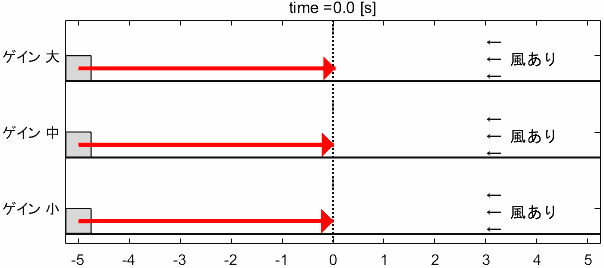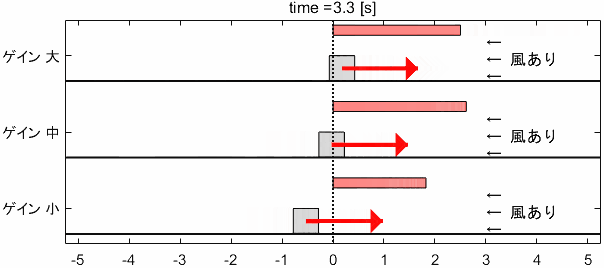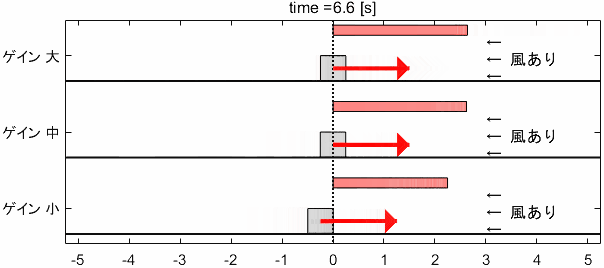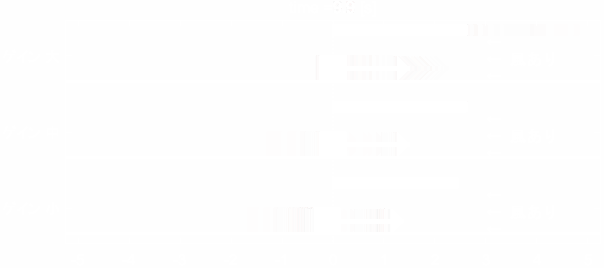
※上部に出ているメーターが、Iの項によって発生している力（$=K_I \int ^t _0 e(\tau) d\tau$）を表しています
ゲイン大は、風力に抗いすぎて一度目標地点を通り過ぎてしまっていますね…。目標地点を通り過ぎた後は誤差がマイナスになるため、マイナスの誤差が蓄積されてメーターが減少し、最終的に風力と釣り合う値に落ち着いていることが見て取れます。
一方、ゲイン小では風力に十分抗えず、目標地点手前で大きく減速してしまっています。その後、誤差の蓄積によりジワジワとメーターが増加し、最終的に風力と釣り合っていることが分かりますね。
まとめると、だいたい次のような傾向が得られました。
- Iゲイン大：外乱に抗いすぎ、目標値を通り過ぎる。
- Iゲイン中：外乱とちょうど釣り合う力を発生させ、目標値でピッタリと止まる。
- Iゲイン小：外乱に抗いきれず、目標値手前で大きく減速する。
位置$y$、入力$u$、Iの項によって発生した力（メーターの値）をそれぞれプロットしたものがこちらです。
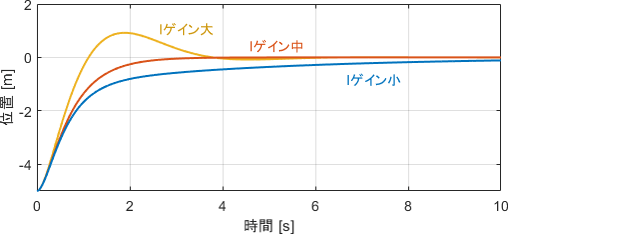
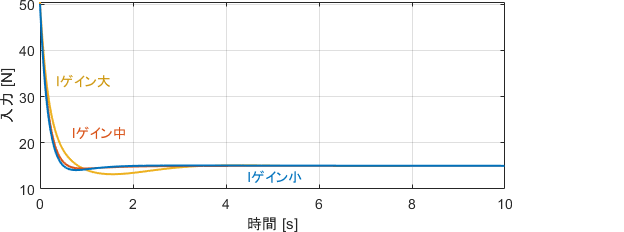
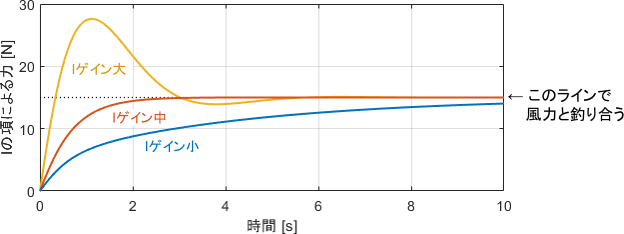
一番下のグラフに注目すると、Iゲインによって「外乱にどのように抗うか」、言い換えると「抗う力をどれくらいの勢いで発生させるか」が調整されていると解釈できますね。
以上、PIDゲインの特性についての解説でした。
※PID系の制御ではゲインチューニングが重視されがちですが、ゲインチューニングは適切な制御器の選択が前提となっているため注意が必要です。制御器の選択方法、およびゲインチューニングの具体的な方法については、こちらのページで詳しく解説していますので、合わせてご覧ください。
- Pゲインが大きい：入力が大きくなり、動作は素早く、振動的になる
- Dゲインが大きい：ブレーキ力が大きくなり、動作は遅く、振動が抑制される
- Iゲインが大きい：外乱に抗う力を、勢いよく発生させる
コメント
すごく参考になります！！
最近、PID制御について調べたりしていましたが一番わかりやすいです。
今後も参考にさせていただきます。
コメントいただき、ありがとうございます。お役に立てたようでなによりです。
記事のトピックで今後何か不明点が生じましたら、ご連絡くださいね。
図示もされていて大変参考になりました。
1点質問させてください。
このページでは制御をt領域の形式で表現されているかと思います。
(リンク先の表記を参考にしました。 https://controlabo.com/transfer-function/)
PID制御を伝達関数として扱う、すなわちs領域で表現する場合について悩んでいます。
s領域のPIDのゲインKp,Ki,Kdはt領域の時と同じ値でしょうか？
あるいはt→sとラプラス変換をする際に係数も何らかの変換が行われ、値としては違うものになるのでしょうか？
自分でラプラス変換してみれば分かりそうな気もするのですが、どこから手を付けてみればいいか分からず…。
どうぞよろしくお願いいたします。
返信が遅れて申し訳ありません。
定数の掛け算の場合、ラプラス変換の前後で値は変わらないため、ゲインとしては同じ値となります。
※こちらのページの「線形性」という性質がそれに当たります。
https://controlabo.com/laplace-transform/#toc12