このページでは、線形システム・非線形システムの違いと、時変システム・時不変システムの違いについて解説します。また、それぞれのシステムの具体例と、実用シーンでの使われ方についても解説します。
- 重ね合わせの原理を満たすのが、線形システム。
- それ以外も含むのが非線形システム。
- システムの性質が時間とともに変化するのが、時変システム。
- 変化しないのが時不変システム。
線形システム
線形システムとは
線形システムとは、線形性を満たすシステムのことです。

お、おう…
線形性って?
線形性とは、重ね合わせの原理を満たす性質です。

お、おう…
重ね合わせの原理って?
順に説明していきましょう。
重ね合わせの原理
まず、あるシステムに$u_1(t)$を入力したときの出力を$y_1(t)$、$u_2(t)$を入力したときの出力を$y_2(t)$とします。
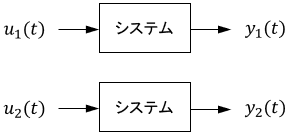
このとき、次の両方を満たす性質を重ね合わせの原理と呼びます。
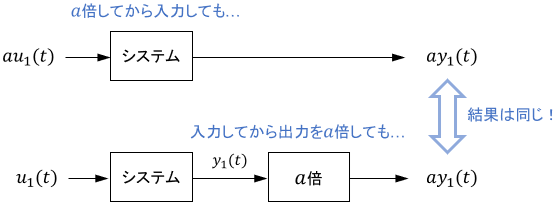
- $au_1(t)$ を入力したときの出力が $ay_1(t)$ ※$a$は実数
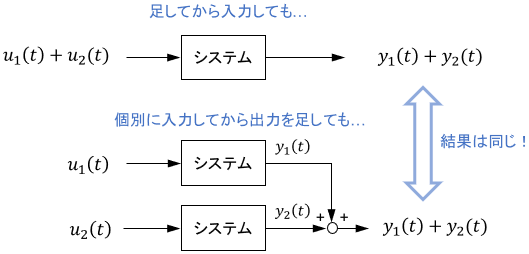
- $\left\{ u_1(t)+u_2(t)\right \}$ を入力したときの出力が $\left\{ y_1(t)+y_2(t)\right \}$

よりかみ砕いて解釈すると、「定数との掛け算」と「信号の足し算」は、入力前にしても出力後にしても、最終結果は変わらないという性質だと言えます。
この性質のおかげで、線形システムは非常に扱いやすく、理論や実用の主役として活用されています。線形性を活かしてシステムを見る「視点」を柔軟に変えることで、様々な観点での分析・設計が可能となるわけですね。
例えば、入力信号をいくつかに分けて別々に分析してから結果を足し合わせたり、逆に出力結果を解析して入力の成分を推定したり、といったことが可能となります。
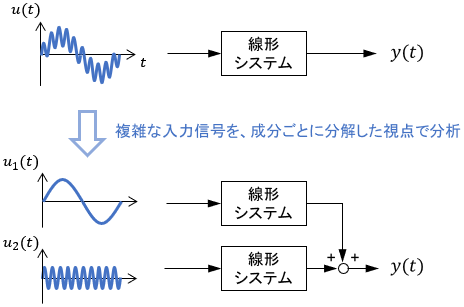
制御の超強力な武器である周波数解析は、まさしくこの線形性を活用しています。線形性によって、システム分析の視点を「時間」から「周波数」に変えているわけですね!
このように、視点を変えてもシステムの振る舞いが破綻しないという「キレイな構造」が線形性の本質です!
※周波数解析の詳細については、こちらのページをご覧ください。ちなみに周波数解析は、線形性に加えて後述の「時不変性」も前提としています。
線形システムの数式モデル
線形システムの多くは、次のような線形微分方程式で表されます(以降、$a_i, b_iは実数$)。
$$ a_2 \ddot{y}(t) \ +\ a_1 \dot{y}(t) \ +\ a_0 y(t) \ =\ b_1 \dot{u}(t) \ +\ b_0 u(t) $$
ざっくり言うと、数式モデルが「係数×信号(の微分)」の項だけで表されるわけですね。(ここでの「信号」は、システムの入力$u(t)$、出力$y(t)$、状態$x(t)$などを指します)
入出力信号が複数ある場合は、連立微分方程式となります。例えば入力が2つ($u_1,u_2$)、出力が3つ($y_1,y_2,y_3$)の場合、次のようになります(以降、$(t)$は省略します)。
$$\left\{ \begin{alignat}{10} \dot{y}_1 &+ & & y_1 & &- 2 & &y_2 & &+ 3 & &y_3 & &= & &u_1 & &+ 2 & &u_2 \\ \dot{y}_2 &- 4 & &y_1 & &+ 5 & &y_2 & &- 6 & &y_3 & &= 3 & &u_1 & &+ 4 & &u_2 \\ \dot{y}_3 &+ 7 & &y_1 & &- 8 & &y_2 & &+ 9 & &y_3 & &= 5 & &u_1 & &+ 6 & &u_2 \end{alignat}\right.$$
線形微分方程式は厳密な解(解析解)をキレイに求められることが多いので、それを糸口にシステムの特性を詳細に分析できることも大きな強みです。
※むだ時間要素 $y(t)=u(t-\tau)$ のように、(有限次元の)線形微分方程式で表されない線形システムもあります。
非線形システム
非線形システムとは
一方の非線形システムは、その名の通り「線形性を満たさない」、つまり重ね合わせの原理を満たさないシステムを指します。
…と言いたいところですが、制御の文脈では「線形システムも含む、一般のシステム全体」を指すことがほとんどです。
そのため実用上は「なんでもいいけど、とにかくここからの議論は線形性をアテにしないよ」ということを強調した呼び方だとイメージしておくとよいでしょう。

※このあたりの分類には様々な流派があるので、絶対的な定義を想定するのではなく「現在の文脈で何を指しているのか」を都度判断するのが間違いありません。
非線形システムの数式モデル
もちろん数式モデルは、線形に限らない様々な形をとります。
線形/非線形のわかりやすい例を見比べて、イメージを深めてみましょう。
$$ \begin{alignat}{5} a_2 \ddot{y} &\ +\ a_1 \dot{y} & &\ +\ a_0 y & &=\ b_1 \dot{u} & &\ +\ b_0 u \ :& & \quad 係数×信号(の微分)のみなので\textbf{線形}\\ a_2 \ddot{y} &\ +\ a_1 \dot{y} & &\ +\ a_0 \color{red}{\sin y }& &=\ b_1 \dot{u} & &\ +\ b_0 u\ :& & \quad 信号の\sin 関数があるので\textbf{非線形} \\ a_2 \ddot{y} &\ +\ a_1 \color{red}{\dot{y}^2} & &\ +\ a_0 y & &= \ b_1 \dot{u} & &\ +\ b_0 u\ :& &\quad 信号の2乗があるので\textbf{非線形} \\a_2 \ddot{y} &\ +\ a_1 \dot{y}^2& &\ +\ \color{red}{a_0 ^2} y & &=\ b_1 \dot{u} & &\ +\ b_0 u\ :& &\quad 係数は2乗しても係数のままなので\textbf{線形} \end{alignat} $$
非線形システムの特徴と実際
非線形システムの強みとしては、やはり様々な対象をカバーできる広い適用範囲が挙げられます。
ただしほとんどの場合、式が複雑すぎて厳密な解を求められないため、設計や分析の難易度は格段に上がります。

非線形システムを制御する際のアプローチとしては、例えば次のようなものが挙げられます。
- コンピュータ計算により強引に解を求める(例:数値計算)
- 厳密解は分からなくとも、制御量だけはなんとか手なずける(例:リアプノフ安定化)
またテイラー展開などを用いて、非線形システムを扱いやすい線形システムに近似することもよく行われます。これによりモデルの精度は下がりますが、線形の制御理論が適用可能となります。
※テイラー展開とそれを用いた近似についてはこちらのページで詳しく説明していますので、合わせてご覧ください
時変システムと時不変システム
線形システム・非線形システムは、さらに時変システムと時不変システムに分けられます。
- 時変システム:性質が時間とともに変化する
- 時不変システム:性質が時間とともに変化しない
数式上では、信号にかかる係数に対して、次のような違いを持ちます。
- 時変システム:係数が時間に直接依存する
- 時不変システム:係数がすべて定数(=時間に依存しない)
$$ \begin{alignat}{5} a_2 \ddot{y} &\ +\color{red}{a_1(t)} & & \dot{y} \ +\ a_0 y & &\ =\ b_1 \dot{u} & &\ +\ b_0 u \ : & &\quad 係数が時間に依存するので\textbf{時変}\\ a_2 \ddot{y}& \ +\ a_1& &\dot{y} \ +\ a_0 y & &\ =\ b_1 \dot{u} & &\ +\ b_0 u\ : & &\quad 係数がすべて定数なので\textbf{時不変} \end{alignat} $$
線形システムは、時変か時不変かによって扱いやすさが大きく変わります(時不変のほうが格段に扱いやすい)。よってこれらを区別するために、それぞれを「線形時変システム」「線形時不変システム」と呼ぶこともあります。
※線形事変システムは、LTVシステム(Linear Time-Varying system)、線形時不変システムはLTIシステム(Linear Time-Invariant system)と略して表記されることも多いです。
一方で非線形システムはもともと複雑なので、線形システムと比較すると、時変であるか時不変であるかによって扱いやすさはそこまで変わりません。よって「非線形時変システム」「非線形時不変システム」と区別して呼ぶことはそんなにありません。(意味は通じますが)
それぞれの扱いやすさのイメージをざっくり図で表すと、次のようになります。

制御の基礎理論で扱うのは、基本的に線形時不変システムのみです。
※ちなみに、線形時不変システムのなかでも特に扱いやすいものを「プロパーなシステム」としてさらに区別することもあります。詳しくは、こちらのページをご覧ください
線形時不変システムの例
例として、次のような機械システムを考えましょう。
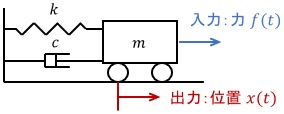
$k$はばね定数、$c$は粘性減衰係数、$m$は質量です。このシステムは、次のように線形時不変システムとしてモデリングできます。
$$ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t) $$
前述の通り、線形時不変システムは一番シンプルで扱いやすいので、まずこれを目指してモデリングが行われます。
実際、実用シーンで目にする線形システムのほとんどは線形時不変システムです。
※こちらのページでは、その他の様々な線形時不変システムを紹介していますので、合わせてご覧ください
線形時変システムの例
先ほど説明した通り、線形システムのほとんどは時不変システムとしてモデリングされるので、線形時変システムが登場する機会は少なめです。ここでは、どのようなときに線形時変システムが使われるのかを解説します。
※少し踏み込んだ説明をするため、線形事変システムに興味がない方は読み飛ばしても構いません。
線形時変な制御対象の例(ほとんどない)
先ほどの機械システムを、再び考えましょう。

今、システムが動作するにつれてばねが徐々に温まり、それに応じてばね定数$k$が$k_0$から$k_f$へ変化するとします。このシステムの運動方程式は、例えば次のように線形時変システムとして表すことができます。
$$ \begin{align}機械システムのモデル:&\quad m\ddot{x}(t) + c\dot{x}(t) + \color{red}{k(t)}x(t) = f(t) \\[3pt] ばね定数のモデル:&\quad \color{red}{k(t)} = (k_0 – k_f) e^{-t} + k_f \end{align}$$
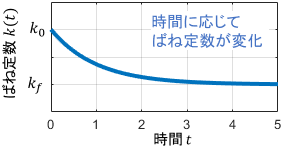
※式は一例なので、詳しく読みとらずにイメージだけ抑えておけばOKです(以降も同じです)
ばね定数を時間の関数$k(t)$として、時間が経つにつれて(上ではだいたい5秒かけて)変化するようにモデリングしているわけですね。
このように、物理パラメータの変化を時間の関数として簡易的にモデリングすることがたまにあります。ただし、これは対象の本質を反映したモデリングにはなっていないことに注意が必要です。
実際のところ、ばね定数は時限爆弾のように時間に直接依存しているのではなく、ばねの温度に依存しているわけですよね。よって動作条件(気温など)が変わればその変化の様子も変わってしまい、上記モデルでは誤差が生じてしまいます。

もし「ばね定数は温度に依存する」という物理的本質をモデルに反映させたい場合は、温度$T(t)$という信号を新たに定義し、ばね定数を温度の関数$k(T(t))$と見なせばよいでしょう。
ただこうする場合は、温度$T(t)$という信号が増え、かつ「温度$T(t)$がどう変化するのか」を表すモデルも別途必要となるため、モデリングや設計の難度が上がってしまいます。
このように、モデリングは方針ごとに利点・欠点があるので、どの方針でモデリングするかはケースバイケースで柔軟に判断する必要があります。そこが設計者の腕の見せ所でもありますが、基本的には物理パラメータを直接時間の関数とすることはほとんどないと考えてよいでしょう。
線形時変な制御器の例(たまにある)
一方で制御器は人が自由に設計するものなので、制御器を線形時変システムとすることはたまにあります。
代表的な例が、制御パラメータ(制御ゲイン)を時々刻々と変化させる場合です。
例として、先ほどの(線形時不変な)機械システムに力$f(t)$を入力し、位置$x(t)$を制御する場合を考えましょう。

$$ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t) $$
力$f(t)$は我々が事前に設計した制御器が作ってくれるものとします。
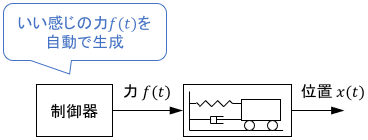
ただこの制御器、なぜかONにした直後にとても大きな力$f(t)$を発生させるため、システムが大きく暴れてしまうとしましょう。

これが起きないように制御器を設計しなおすのが本質的な解決策ですが、ここでは簡易的な解決策として、制御をいきなりONにするのではなく徐々に有効化させることを考えましょう。
まず、我々が最終的な力の大きさ(制御の効き具合)を調整できるように、制御ゲイン$K$を次のように導入します。

つまり、最終的には調整後の $Kf(t)$ が入力として機械システムに与えられるわけですね。

$$ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = \color{green}{\usg{K}{追加}} f(t) $$
ゲイン$K$が定数であれば、このシステムは線形時不変システムのままです。
ここで$K$を時間の関数$K(t)$として、時間がたつにつれて徐々に0から1へ立ち上がらせると、徐々に制御を有効化させる挙動が実現可能となります。

数式モデルの構造に着目すると、$K(t)$によってシステムが線形時変システムとなっていますね!
$$ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = \color{red}{K(t)} f(t) $$
このように「時間に応じて制御のかかり具合を調整したい」といった用途で、制御器を時変システムにすることがあります。
もちろん「時間に直接依存させるのが本当に適切か?」といった検討は別途必要となりますが、制御方針の選択肢の一つとして知っておくとよいでしょう。
※ちなみに上記は「ゲインスケジューリング」と呼ばれる制御手法の一種だとも解釈できます
非線形システムの例
単純な非線形システムの例としては、振り子が挙げられます。
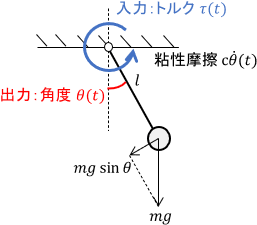
このシステムは、次のように非線形な運動方程式で表されます。
$$ml^2 \ddot{\theta} + c \dot{\theta} + mgl \ubg{\sin \theta }{非線形} = \tau$$
ちなみに入出力以外の係数が全て定数なので、これは時不変なシステムです。
前述の通り、非線形システムはテイラー展開などを用いて線形近似することがよく行われます。上の振り子を線形近似すると、次のようになります。
$$\begin{gather} \sin \theta \approx \theta と近似すると、 \\[5pt] ml^2 \ddot{\theta}+ c \dot{\theta} + mgl \theta = \tau \quad \color{green}{線形になった!}\end{gather}$$
以上、線形システム・非線形システムの違いと、時変システム・時不変システムの違いについての解説でした。
- 重ね合わせの原理を満たすのが、線形システム。
- それ以外も含むのが非線形システム。
- システムの性質が時間とともに変化するのが、時変システム。
- 変化しないのが時不変システム。





