制御で扱うシステムは大きく動的システム(ダイナミカルシステム)と静的システム(スタティックシステム)に分けられます。
このページでは、それぞれの違いと直感的イメージを解説します。
- 静的システム:結果を一瞬で返すもの。代数方程式で表される。
- 動的システム:一定の結果を返すのに時間がかかるか、一定の結果に至らないもの。微分方程式で表される。
- 一定の結果を返すまでが「実質的に一瞬」と見なせるなら、動的システムでも「実質的に静的システム」とみなせる。
直感的イメージ。カギは「結果」が一瞬で得られるかどうか!
今、あるシステムにステップ入力を与えたとします。例えば、ある瞬間に「はい動け!」とスイッチを入れた場合がこれに当たります。
このとき、「はいよ!」と一瞬で結果を返すのが静的システム、結果に至るまでに時間がかかるか、一定の結果に至らないものが動的システムです。

※ステップ入力とステップ応答の詳細については、こちらの記事をご覧ください。
静的システムの例
抵抗
次のような超単純な電気システムは静的システムです。
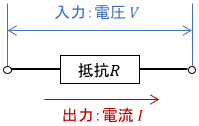
ある瞬間にスイッチを押して電圧$V$を入力する(ステップ入力を与える)と、出力である電流$I$は瞬時に決定されます。そこに過程は存在しません。
このシステムを表す式は、オームの法則ですね。
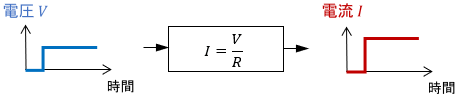
この式に従い、電圧$V$に対して電流$I$が問答無用で決定されるわけです。
ばね
ばねも静的システムと解釈することができます。
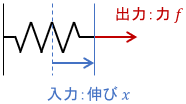
入力であるばねの伸び$x$に対し、出力である力$f$は瞬時に決定されます。
このシステムを表す式は、フックの法則ですね。
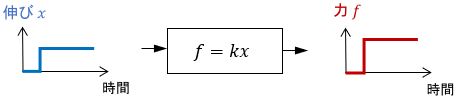
以上のように、静的システムは代数方程式(普通の方程式)によって表され、それを解くことで結果が「値」として瞬時に求まります。
動的システムの例
台車
次のように、台車に力を与えることで速度を発生させるシステムは、動的システムです。

ある瞬間から力$f$を台車に入力し続ける(ステップ入力を与える)と、出力である速度$v$は徐々に増加し、やがて一定値に至ります。
当然、結果に至るまでに「加速」という過程が生じますよね。これが動的システムの特徴です。
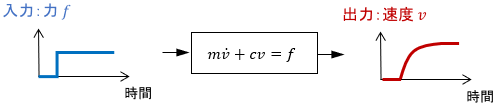
これは、入力に対して出力が「遅れる」とも表現されます。
システムの挙動は、上図の通り運動方程式で表されます。この運動方程式を解くことで、時々刻々変化する速度が時間の関数$v(t)$として求まるわけですね。
ばねマスシステム
次に、ばねに質点がついたシステムを考えましょう。
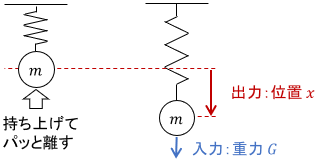
質点を持ち上げ、ある瞬間にパッ!と手を離したとします。この場合、手を離した瞬間から質点には重力$G$が与えられ続けます(つまりステップ入力)。
摩擦や空気抵抗がない場合、質点はビヨビヨ振動し続け、いつまで経ってもその位置は1つに定まりません。
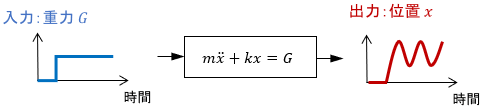
このように、動的システムは必ずしも一定の出力を返すわけではありません。
ちなみにこのシステムの挙動も、上図の通り運動方程式で表されます。
以上のように、動的システムは微分方程式によって表され、それを解くことで時々刻々変化する挙動が「時間の関数」として求まります。
実質的に静的システムとみなせる場合
ここまで、静的システムは「結果を一瞬で返すシステム」と説明してきました。
この「一瞬」というのは、「メインの制御対象の動作に比べて無視できるほど速い」という意味です。よって、メインの制御対象に比べて超速く結果を返せるシステムは、それが動的システムでも実質静的システムと解釈してよい場合があります。
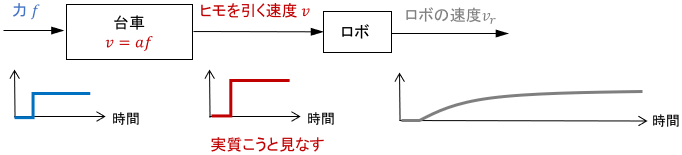
例で見てみましょう。下に示すのは、先ほどの台車が含まれたシステムです。台車がヒモを引っ張ると、引っ張る速さに応じてロボットがのそ~っと歩く、という謎のシステムであるとします。

このシステムのブロック線図と各変数の応答を、次に示します。
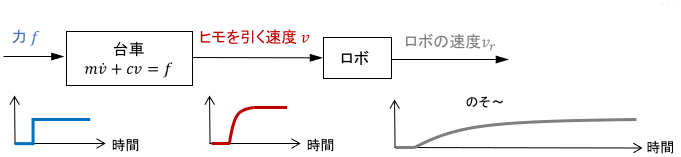
台車の反応は、ロボットの反応に対して超速いですね。この場合は台車の挙動を運動方程式で厳密に考えずに、「台車は力$f$に応じた速さ$v$で一瞬で走りだす」と考えてもほとんど問題ありません。
よって、台車の挙動は次のように代数方程式で単純化(近似)できます。
当然、微分方程式よりも代数方程式のほうが扱いが楽なので、このほうがシステムや制御の設計が簡単になります。
このように「無視できる情報は積極的に無視してシステムを単純化する」という手法はシステム設計にて非常に多く用いられますので、覚えておいてくださいね。(とはいえ、やりすぎると誤差が増大してしまいます。どこまで無視するかは設計者の腕の見せ所となります。)
以上、動的システムと静的システムの違いと直感的イメージについての解説でした。
- 静的システム:結果を一瞬で返すもの。代数方程式で表される。
- 動的システム:一定の結果を返すのに時間がかかるか、一定の結果に至らないもの。微分方程式で表される。
- 一定の結果を返すまでが「実質的に一瞬」と見なせるなら、動的システムでも「実質的に静的システム」とみなせる。




コメント