This page explains the stability of a system, an essential property in control engineering. Particularly, the intuitive concept rather than the mathematical definition will be explained in detail.
- (Most) stable systems stop when left alone without any input.
- Unstable systems return divergent outputs when left alone without any input.
- There are various types of stability, but they can be considered almost the same.
Intuitive Meaning of Stability
Stable System
Generally speaking, a stable system is one whose output (and state) does not diverge even when left alone without any input.
Since most real systems converge to the state of “stop,” you can intuitively imagine a stable system as a system that stops if left alone without any input.
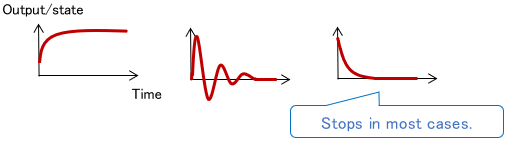
Note: Assume the system is not in a state of equilibrium (convergence destination) at first. For example, we do not consider the case where a stopped system is left alone and remains stopped.
Unstable System
An unstable system is one whose output (and state) diverges if left alone without any input.
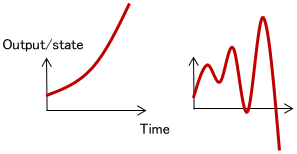
Let’s look at examples of each.
Examples of Stable Systems
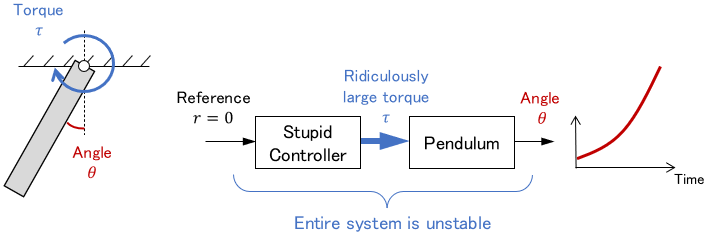
Pendulum
A pendulum is a stable system because it will stop due to friction if left alone.
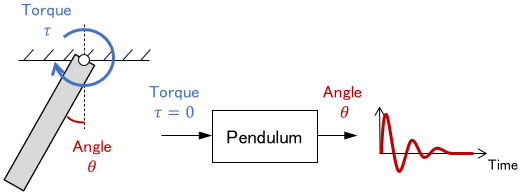
Not only pendulums but most mechanical systems are stable on their own. If left alone, they will generally stop. (Examples of unstable systems will be introduced later.)
Electric Circuit
A simple circuit such as an RLC circuit is also stable because it will stop working if switched off (i.e. if no input is given).
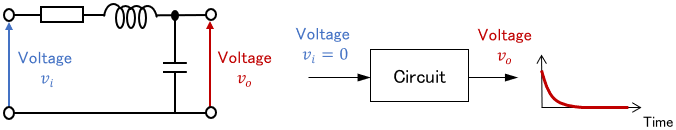
Like mechanical systems, electrical systems are mostly stable on their own. They stop working when you turn off the switch.
Examples of Unstable Systems
Drone
A drone is an unstable system because it will fall if left alone and do nothing.

If there is no ground, it will keep falling infinitely, and the state will not converge.
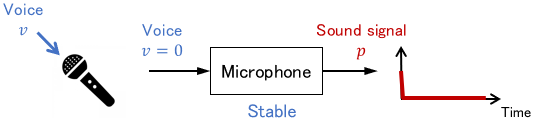
Microphone Feedback
When a microphone picks up the sound from a loudspeaker, the sound is amplified infinitely, and you get feedback.
Even if nothing is voiced (i.e. no input is given), the feedback will not end, which makes the whole system unstable.

Note the Scope when Considering Stability
Note that stability depends on the scope of the system you are looking at.
For example, the drone mentioned earlier was an unstable system on its own, but if the controller is properly designed, the entire system will be stabilized.
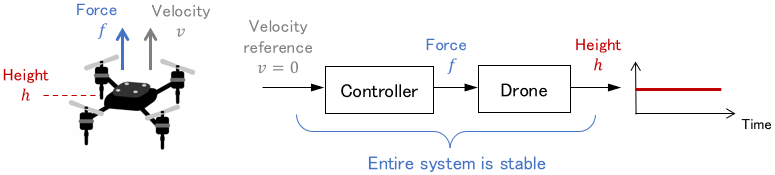
Also, microphone feedback was unstable for the entire system, but the microphone itself is a stable system.
The pendulum was also stable on its own, but it can easily become unstable when connected to a stupid controller.
As mentioned above, when thinking about stability, always be aware of what scope you are looking at now.
Types of Stability
Actually, there are many different types of stability in control engineering. Let’s look at some typical examples.
Stability based on Poles
This stability focus on whether the output (and state) will diverge if left alone without input.

This is the same as what we have been considering. It is known that this stability can be theoretically discriminated by parameters called poles of the system.
Stability based on Step Response
This stability is based on whether the output (and state) diverges if left alone with a step input.
Since there is an input, it is unlikely that the system will converge to a “stop” state. You can imagine it as whether or not the system will settle into some steady state with constant input.

BIBO Stability
Stability based on whether the output is bounded for a bounded input is called Bounded-Input-Bounded-Output stability.

These three types of stability are known to be equivalent for proper systems*. So, you can consider that there are many kinds of stability, but in most cases, they are practically the same.
*Simply put, “proper systems” are the kind of systems you would find in a basic control engineering textbook. For more information, please see this page.
- (Most) stable systems stop when left alone without any input.
- Unstable systems return divergent outputs when left alone without any input.
- There are various types of stability, but they can be considered almost the same.



Comments