This page describes the transfer function of higher-order systems and their intuitive concepts.
- Most higher-order systems can be expressed by combining basic systems.
- If an output of one system is an input to another system, the overall higher-order transfer function can be created by simply multiplying their transfer functions together.
- Otherwise, the transfer function can be derived by organizing differential equations.
- The poles of a higher-order system are equal to the poles of the basic systems that compose it.
What is Higher-Order System?
A system whose mathematical model is represented by a third-order or higher differential equation is called a higher-order system. Higher-order systems often consist of several simple systems.
It is also known that most higher-order systems can be represented by a combination of basic systems, i.e. first-order systems, second-order systems, integral systems, proportional systems, and so on.

Note: For more information about the basic systems and their transfer functions, please see this page:
Get the Picture with a Simple Example!
Basic Concept of Higher-Order System
Consider a system in which a cart is moved by wind force from a propeller, as shown below.
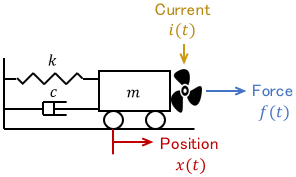
The propeller generates wind force $f(t)$ according to the input current $i(t)$. The cart then receives the force $f(t)$ and changes its position $x(t)$ (i.e. moves).
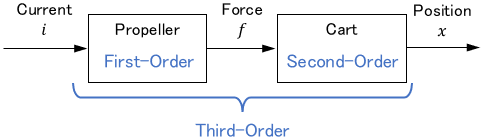
In this case, the block diagram of the entire system is expressed as follows.

Note that the output of the propeller is directly inputted to the cart.
If the propeller is a first-order system and the cart is a second-order system, the entire system becomes a third-order system, as calculated later.
Before the calculations, let’s understand this intuitively. The main part of the above system is the cart. However, the model (block) of the cart itself assumes that the force $f(t)$ is freely given without any constraints (e.g., the desired force can be given immediately without any delay.)
Of course, in reality, it is impossible. Therefore, by adding the propeller model in front, a practical model that also considers the characteristics of $f(t)$ (e.g., delay) is constructed. As a result, the entire system becomes a higher-order system (third-order system).
Derivation of Transfer Function
Now let’s actually calculate the transfer function of the above system and confirm that the entire system is third-order.
First, the equation of motion of the cart is expressed as
$$m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t).$$
The input is the force $f(t)$, and the output is the position $x(t)$. Since it is a second-order differential equation, the cart is a second-order system. By finding the Laplace transform of this, we obtain the transfer function $G_1(s)$ of the cart.
$$X(s) = \ubg{\frac{1}{ms^2 + cs + k}}{\large G_1(s)}F(s)$$
On the other hand, let the propeller characteristics be expressed as
$$\dot{f}(t) + a f(t)= i(t).$$
The input is the current $i(t)$ to the propeller, and the output is the wind force $f(t)$. Since it is a first-order differential equation, the propeller is a first-order system. By finding the Laplace transform of this, we obtain the transfer function $G_2(s)$ of the propeller.
$$F(s) = \ubg{\frac{1}{s+a}}{\large G_2(s)} I(s)$$
Combining them yields the transfer function $G(s)$ for the entire system.
$$\begin{align}X(s) &= G_1(s) \cdot G_2(s) \cdot I(s)\\\\ &= \frac{1}{ms^2 + cs + k} \cdot \frac{1}{s+a} I(s)\\\\ &= \ubg{\frac{1}{ms^3 + (c+ma)s^2 + (k+ca)s + ka}}{\large G(s)} I(s)\end{align}$$
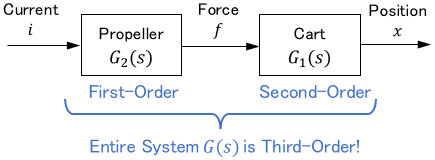
The entire system turns out to be a third-order system. Since this system is a simple combination of second- and first-order systems, we can express the entire characteristics simply by multiplying the transfer functions.
Thus, we can interpret a higher-order system as a system obtained by combining the basic systems.
Poles of Higher-Order System
Next, let us consider the poles of the system.
For simplicity, let the poles of the cart $G_1(s)$ be $p_1$ and $p_2$, and the pole of the propeller $G_2(s)$ be $p_3$. Then, the transfer function $G(s)$ of the entire system can be represented as follows.
$$\begin{align}G(s) &= G_1(s) \cdot G_2(s)\\[5pt] &= \ubg{\frac{\alpha}{(s-p_1)(s-p_2)}}{\large G_1(s)} \cdot \ubg{\frac{\beta}{s-p_3}}{\large G_2(s)}\\[5pt]&= \frac{\alpha\beta}{(s-p_1)(s-p_2)(s-p_3)} \end{align}$$
where $\alpha$ and $\beta$ are the components resulting from the transformation.
It is important to note that the poles of the entire system $G(s)$ are $p_1$, $p_2$, and $p_3$, which inherit the poles of $G_1(s)$ and $G_2(s)$.
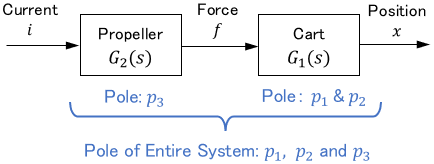
In other words, the poles of a higher-order system are equal to the poles of each system that constitutes it. Since the poles are parameters that represent the characteristics of a system, we can interpret that the higher-order system inherits the characteristics of each of the systems that constitute it.
Complex Example. Essentially the Same!
In the previous example, the output of one system was directly inputted to the other. Therefore, the transfer function of the entire system could be derived simply by combining the transfer functions of the individual systems.
In fact, this becomes impossible when the system becomes more complex. But the basic concept remains the same. Let’s look at the details with an example.
Derivation of Transfer Function
On the previous example, let us change the propeller characteristics to the following equation.
$$\dot{f}(t) + a f(t) + \ubg{b\dot{x}(t)}{\text{Added}} = i(t)$$
The output $f(t)$ now depends not only on the current $i(t)$ but also on the velocity $\dot{x}(t)$ of the cart. In this case, the equation is based on three variables: current $i(t)$, force $f(t)$, and position $x(t)$. Therefore, we cannot express the input-output relationship simply as in the previous case.
In this case, the block diagram would look like this:
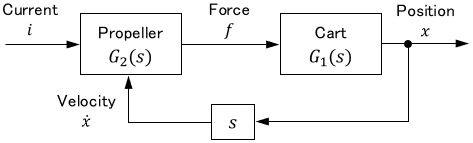
So it becomes more complicated because the motions affect each other.
$$ \left\{ \begin{array}{ll} m\ddot{x}(t) + c\dot{x}(t) + kx(t) = f(t) &: \quad \text{Equation of Cart}\\[3pt] \dot{f}(t) + a f(t) + b\dot{x}(t) = i(t)&: \quad \text{Equation of Propeller} \end{array} \right. $$
From these equations, let’s calculate the transfer function $G(s)$ for the entire system. We cannot combine the transfer functions as before, but we can simply solve the equations for $I(s)$ and $X(s)$.
The Laplace transform of each equation becomes
$$ \left\{ \begin{array}{ll} (ms^2 + cs + k)X(s) = F(s)\\[3pt] (s+a)F(s) + bsX(s) = I(s). \end{array} \right. $$
Substitute the first equation into the second equation to eliminate $F(s)$.
$$ \Bigl\{ (s+a)(ms^2 + cs + k)+bs \Bigr\}X(s) = I(s) $$
After organizing the equation, we obtain the transfer function $G(s)$.
$$\begin{align}X(s) &= \frac{1}{(s+a)(ms^2 + cs + k)+bs} I(s)\\\\ &= \ubg{\frac{1}{ms^3 + (c+ma)s^2 + (k+ca+b)s + ka}}{\large G(s)} I(s)\end{align}$$
The entire system is now third-order. It is a little more complicated, but since it is essentially a combination of first- and second-order systems, the concept is the same as the previous example.
Poles of the System
So what are the poles of this system?
In this case, the entire transfer function $G(s)$ could not be expressed by a simple combination of the lower systems $G_1(s)$ and $G_2(s)$. In other words, $G(s)$ does not have the poles of $G_1(s)$ and $G_2(s)$.
Since we know that the entire system is third-order, it is certain that the entire system has three poles. Therefore, if we let those poles be $p_1$, $p_2$ and $p_3$, $G(s)$ can be transformed as follows.
$$\begin{align}G(s) &= \frac{1}{ms^3 + (c+ma)s^2 + (k+ca+b)s + ka}\\\\&= \frac{\alpha}{(s-p_1)(s-p_2)(s-p_3)}\end{align}$$
So the entire system can be expressed by either of the following combinations.
Combination 1
- First-order system $\frac{1}{s-p_1}$ with pole $p_1$
- First-order system $\frac{1}{s-p_2}$ with pole $p_2$
- First-order system $\frac{1}{s-p_3}$ with pole $p_3$
Combination 2
- First-order system $\frac{1}{s-p_1}$ with pole $p_1$
- Second-order system $\frac{1}{(s-p_2)(s-p_3)}$ with poles $p_2$ and $p_3$
Note: In fact, both combinations are possible. The difference between each will be explained shortly.
In other words, even a complex system can eventually be expressed as a combination of the basic systems.
In the above case, each lower system does not have a one-to-one correspondence with the physical configuration. We can interpret that the underlying characteristics appear as poles of the basic systems, and their combination represents the entire system.
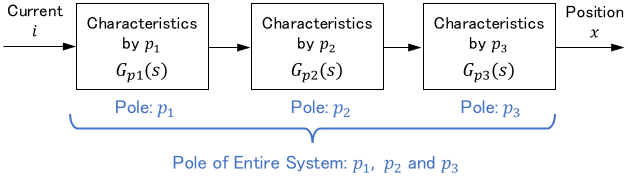
By applying the same concept, even higher-order systems can be expressed by combining the basic systems.
Representing second-order system with two first-order systems

Can’t a second-order system always be represented by two first-order systems?
Thus, can’t the above third-order system be represented by three first-order systems?
The expression of second-order systems can be summarized as follows.
- A second-order system with only real poles can be decomposed into two first-order systems.
- A second-order system with complex poles cannot be decomposed, and it becomes a basic element.
Let’s take a closer look at this. First, when a system behaves oscillatory, it has complex poles. Also, the complex poles always appear in conjugate pairs $p_1=a+bj$ and $p_2=a-bj$, where $j$ is an imaginary unit and $a$ and $b$ are real numbers.
Now, if a first-order system $G_{1st}(s)$ has a complex pole $p_1=a+bj$, then the transfer function becomes
$$G_{1st}(s)=\frac{1}{s-p_1}=\frac{1}{s-\ubg{(a+bj)}{\large \text{Complex}}}.$$
So the transfer function must have a complex number. Of course, in reality, no system with such a transfer function exists.
On the other hand, if a second-order system $G_{2nd}(s)$ has complex conjugate poles $p_1=a+bj$ and $p_2=a-bj$, then the transfer function becomes
$$\begin{align}G_{2nd}(s)&=\frac{1}{(s-p_1)(s-p_2)}\\\\&=\frac{1}{\bigl\{s-(a+bj)\bigr\}\bigl\{s-(a-bj)\bigr\}}\\\\&=\ubg{\frac{1}{s^2-2as+(a^2+b^2)}}{\large \text{Not Complex!}}.\end{align}$$
In this case, the transfer function can be expressed with real numbers only. This means that such a system can exist in reality.
From the above, we can see that the smallest system with complex poles is a second-order system. So this is the reason why the basic system includes the second-order system.
Of course, no such problem occurs if the system has only real poles. So a second-order system can be decomposed into two first-order systems.
This page described the transfer function of higher-order systems and their intuitive concepts. Please also see the page below for examples of higher-order systems often used in practical situations.
- Most higher-order systems can be expressed by combining basic systems.
- If an output of one system is an input to another system, the overall higher-order transfer function can be created by simply multiplying their transfer functions together.
- Otherwise, the transfer function can be derived by organizing differential equations.
- The poles of a higher-order system are equal to the poles of the basic systems that compose it.




Comments