Dynamic vs. Static System – Differences, Usage, and Examples

Systems treated in control engineering can be broadly grouped into dynamic systems and static systems.

This page explains the differences and intuitive concepts of each system through examples.

Intuitive Concept – The key is whether the result is instantaneous!

Suppose a system is given a constant (step) input. This is like turning on a switch at a certain moment.

Against such input, a static system returns a result instantly, while a dynamic system takes time to reach a result or does not reach a particular result.

Examples of Static Systems

Electric Resistance

The following very simple electrical system is a static system.

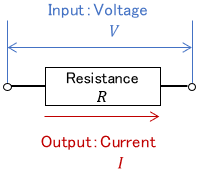
When a voltage $V$ is inputted by pressing a switch (i.e. given a step input), the output, current $I$, is determined instantaneously. There is no process involved.

The equation for this system is Ohm’s law.

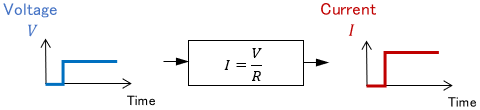
According to this equation, the current $I$ is uniquely determined for a voltage $V$.

Spring

Spring can also be interpreted as a static system.

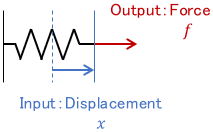
The output force $f$ is instantaneously determined for the input spring displacement $x$.

The equation that represents this system is Hooke’s law.

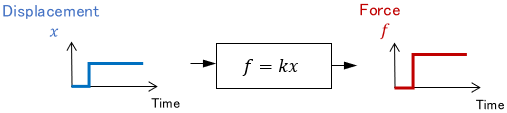
As shown above, static systems are represented by algebraic equations, and by solving them, the result is instantly obtained as a value.

Examples of Dynamic Systems

Cart

As shown below, a cart that generates speed by applying force is a dynamic system.

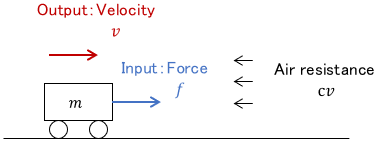
If a constant force $f$ is continuously input to a cart (i.e. a step input is given), the output velocity $v$ gradually increases and eventually reaches a constant value.

Obviously, there is a process of acceleration before reaching the result. This is a characteristic of dynamic systems.

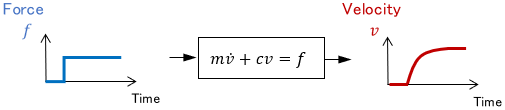
Such behavior is also described as the output being “delayed” from the input.

The system characteristic is expressed by the equation of motion, as shown above. By solving this, we can obtain the velocity, which changes from time to time, as a function of time, $v(t)$.

Spring-Mass System

Next, let’s consider a system with a mass point attached to a spring.

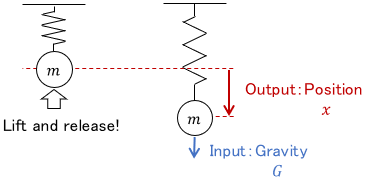
Let’s assume you lift a mass point and release your hand. In this case, from the moment you release your hand, the mass is continuously subjected to gravity $G$ (i.e. step input).

If there is no friction and air resistance, the mass point will continue to oscillate, and its position will not settle.

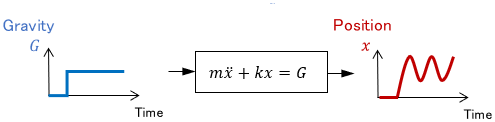
Thus, a dynamic system does not always return a constant output in the end. Incidentally, the behavior of this system is also expressed by the equation of motion.

As described above, dynamic systems are represented by differential equations, and by solving these equations, the ever-changing behavior can be obtained as a function of time.

Case in which the system can be regarded as practically static

So far, we have described a static system as “a system with instantaneous results”.

The “instantaneous” here means “negligibly fast compared to the main system’s behavior.” Therefore, a system that returns results much faster than the main system can be interpreted as a practically static system, even if it is essentially a dynamic system.

Let’s look at an example. Shown below is a system that includes the cart we saw earlier. Suppose it is a strange system in which when the cart pulls the rope, the robot walks slowly according to the speed of the pull.

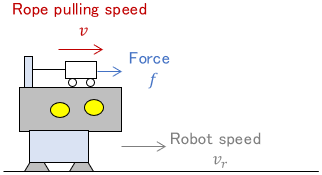
The following is a block diagram of this system and the response of each variable.

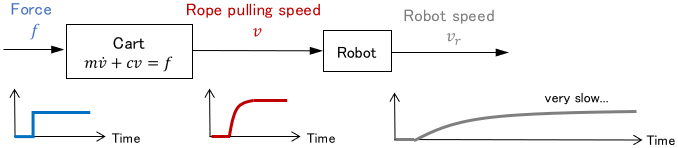
The response of the cart is much faster than the robot’s response. In this case, instead of considering the cart’s behavior strictly by the equation of motion, it is okay to consider that the cart starts running immediately at a speed $v$ corresponding to the force $f$.

Therefore, the behavior of the cart can be simplified (approximated) by the algebraic equation as follows:

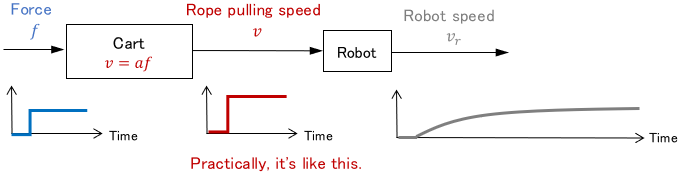
Naturally, an algebraic equation is easier to handle than a differential equation, so this simplifies the control design itself.

Such a technique of simplifying the system by actively ignoring unimportant information is very often used in control system design.

However, care must be taken because ignoring too much information can increase errors. It is up to the designer to decide how much to ignore, and this is where the designer’s skill comes into play.