Angular frequency is a crucial entity in physics or control engineering, but it can be difficult to interpret if you are unfamiliar with it. This page explains the intuitive meaning and use of angular frequency.
- Angular frequency is a coefficient that appears when expressing oscillation with a sine (or trigonometric) function.
- Specifically, it is a physical quantity that expresses how many radians take place in the sine function every second.
- By using angular frequency, oscillation can be described briefly as \(\sin \omega t\).
Review of Frequency
Prior to learn angular frequency, let’s first review the frequency. If you are already familiar with it, please move forward to the next section.
Frequency defines the speed of oscillation and is expressed by $f$. More specifically— how many times it oscillates per second. Frequency describes various vibration phenomena, such as the oscillation of light, sound, electricity, and machinery.
The unit of frequency is hertz (Hz). For example, a 1 Hz wave oscillates once per second, and a 3 Hz wave oscillates three times per second.
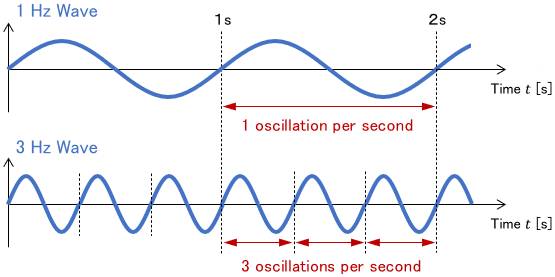
Another interpretation is as follows: number of waves in one second. Therefore, time period of oscillation is the inverse of the frequency.
$$T=\frac{1}{f}$$

Similarly, frequency $f$ can be calculated from the period $T$.
$$f=\frac{1}{T}$$
As reciprocal of time period is frequency, the unit “Hz” equates “1/s”, which can be interpreted as exactly what it means: “number of oscillations per second.”
What is Angular Frequency?
Let’s come to angular frequency. Although angular frequency can be interpreted in many ways, here we present one that is useful for practical use in physics or control engineering.
In a nutshell, angular frequency is a coefficient that appears when expressing oscillation with a sine function. Specifically, angular frequency is the product of freq. $f$ and angle $2\pi$:
$$\text{Angular frequency } \omega = 2\pi f$$
Let’s take a closer look at the reasons for this.
Expression of 1 Hz Sinusoidal Wave
Let’s consider plot of a 1 Hz sinusoidal wave. A plot of a function \(\sin x\) is shown below:
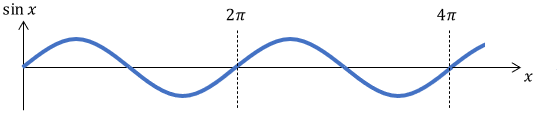
The plain sinusoidal wave oscillates once per $2 \pi$. So, at the frequency of 1 Hz, we should put 1 rotation (i.e. $2 \pi$) into the sine function every second.

Therefore, a mathematical formula for sine wave of 1 Hz is as follows:
$$\text{1 Hz sine wave} = \sin \left( 2 \pi \cdot t \right)$$
Expression of 3 Hz Sinusoidal Wave
For more insights, let’s consider a 3 Hz sinusoidal wave. Since it oscillates three times per second, we can put three rotations of $2 \pi$ into the sine function every second.

Therefore, if we express a 3 Hz sine wave with a mathematical formula, it looks like this:
$$\text{3 Hz sine wave}=\sin \left( 2 \pi \cdot 3 \cdot t \right)$$
Generalization Reveals Angular Frequency!
Let’s generalize further by considering a sine wave of frequency $f$. Since it oscillates $f$ times per second, we can put $f$ rotations of $2 \pi$ into the sine function every second, and we’re done!
$$\text{Sine wave at freq. }f = \sin \left( 2 \pi f \cdot t \right)$$
So, when dealing with oscillations of freq. $f$ in physics or control engineering, this formula appears very often. But it is quite tedious to write \(\sin \left( 2 \pi f \cdot t \right)\) every time, isn’t it?
No worry! Eventually, \(2\pi f\) is a constant, so let’s express it briefly with a symbol \(\omega\). This \(\omega\) is the angular frequency.
$$\begin{gather} \text{Angular frequency } \omega = 2\pi f \\\\ \sin \left( 2 \pi f \cdot t \right) = \usg{\sin \left( \omega t \right)}{\large \text{Brief!}} \end{gather}$$
Intuitively, the angular frequency is a physical quantity that expresses how many radians take place in sine function every second (i.e. rate of change in rotations.)
The unit of angular frequency is rad/s. This is consistent with the above interpretation.
Angular Frequency Formulas
Finally, let’s look at some formulas to keep in mind when using angular frequencies.
First is the formula to obtain frequency $f$ from angular frequency $\omega$.
$$f = \frac{\omega}{2\pi}$$
Where, $\omega$ expresses $2 \pi f$ rotations every second, dividing it by angle $2 \pi$ gives the freq. $f$. It is clear from the definition of angular frequency.
Next formula is—Time period from the angular frequency.
$$T = \frac{2\pi}{\omega}$$
Since time period is the reciprocal of the frequency, we just turned the previous formula upside down.
Rather than memorizing these formulas, it is important to understand the meaning of angular frequency and be able to derive them on your own.
- Angular frequency is a coefficient that appears when expressing oscillation with a sine (or trigonometric) function.
- Specifically, it is a physical quantity that expresses how many radians take place in the sine function every second.
- By using angular frequency, oscillation can be described briefly as \(\sin \omega t\).


Comments